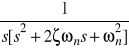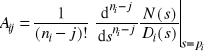WYKŁAD 1:

TRANSFORMATA LAPLACE'A

Przykłady

Przykład 1 (powtórka z Laplace'a)

Rozwiąż równanie różniczkowe
,
oraz
.

Rozwiązanie

Po L-transformacji mamy
a zatem

. (1)

Bieguny transformaty Y(s) są więc biegunami pojedynczymi. Rozkładając Y(s) na ułamki proste, otrzymujemy

. (2)

Rozwiązanie w dziedzinie czasu wyznaczamy, dokonując odwrotnej L-transformacji:

. (3)

Sprawdźmy otrzymany wynik, korzystając ze wzorów Haeviside'a.

, (4)

, (5)

. (6)

Zatem, uwzględniając (5) otrzymujemy wyrażenie dane wzorem (3).

Przykład 2 (powtórka z Laplace'a)

Rozwiąż równanie całkowo-różniczkowe
z warunkiem początkowym
.

Rozwiązanie

Dokonując L-transformacji, otrzymujemy
. Skąd wynika
, a następnie (por. Dodatek 1):
.

Przykład 3 (powtórka z Laplace'a)

Rozwiąż niejednorodne równanie różniczkowe
, zakładając, że warunki początkowe mają postać
,
oraz
, zaś
.

Rozwiązanie

Korzystając ze wzorów

, (1)

, (2)

, (3)

otrzymujemy

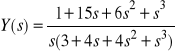
. (4)

Rozkładając (4) na ułamki proste, uzyskujemy

. (5)

Stąd
.

Zadania do samodzielnego rozwiązania (powtórka z Laplace'a)

Zadanie 1

Posługując się metodą transformacji Laplace'a, znajdź rozwiązanie jednorodnego równania różniczkowego
,
,
.

Odpowiedź

Poszukiwane rozwiązanie ma postać:
,

Zadanie 2

Posługując się metodą transformacji Laplace'a, znajdź rozwiązanie niejednorodnego równania różniczkowego
,
,
.

Odpowiedź

Rozwiązaniem jest
,

Zadanie 3

Schemat ideowy pokazany na rys. z1 jest modelem rzeczywistego układu różniczkującego.

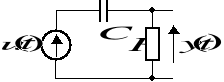
Rys. z1. Obwód RC

Oblicz odpowiedź tego układu na pobudzenie skokowe
, jeżeli na pojemności C znajduje się ładunek początkowy
.

Odpowiedź

Odpowiedź układu ma postać
,
, gdzie
oraz
.

Zadanie 4

Model obiektu ma postać
, przy czym warunki początkowe są zerowe. Zakładając sygnał wejściowy
,
, wyznacz sygnał y(t).

Odpowiedź

Rozwiązanie ma postać
,
.

Zadanie 5

Rozwiąż układ niejednorodnych równań różniczkowych

,

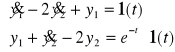
Odpowiedź

Rozwiązaniem jest
,
,
.

Zadanie 6

Wyznacz oryginał transformaty
,
.

Odpowiedź

Rozwiązanie ma postać
,
.

Podstawowe reguły transformacji Laplace'a

W Tablicy D1 podano definicje prostego oraz odwrotnego przekształcenia Laplace'a, a następnie podano podstawowe własności tych przekształceń. Tablica D2 zawiera wybrane (najczęściej spotykane w praktyce) pary odpowiadających sobie oryginałów i obrazów. Wreszcie w Tablicy D3 podano wzory, ułatwiające znajdowanie oryginałów dla obrazów w postaci funkcji wymiernych.

Transformata Laplace'a
Odwrotna transformata Laplace'a
Liniowość
Podobieństwo	,
Przesuniecie argumentu oryginału
Przesuniecie argumentu obrazu
Transformata pochodnej
Transformata wyższych pochodnych
Transformata całki
Transformata całki iterowanej
Granica oryginału w zerze
Granica oryginału w nieskończoności
Transformata splotu oryginałów
Całka Duhamela
Różniczkowanie obrazu
Wyższe pochodne obrazu
Splot obrazów

Tablica D1. Własności przekształcenia Laplace'a

,
,
,

Tablica D2. Oryginały i transformaty Laplace'a

Funkcja wymierna o biegunach jednokrotnych	, , , ,
Funkcja wymierna o biegunach jednokrotnych i biegunie w zerze	, , , , , ,
Funkcja wymierna o biegunach wielokrotnych	, , , , , .

Tablica D3. Wyznaczanie odwrotnych transformat Laplace'a funkcji wymiernych

3

---