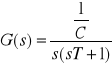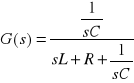OPRACOWANIE PYTAN

1. Co to jest transmitancja operatorowa?

Transmitancje operatorową oznaczamy jako G(s). Przy czym dla układów jednowymiarowych jest to stosunek prawostronnej transformaty Laplace`a sygnału wyjściowego do prawostronnej transformaty Laplace`a sygnału wejściowego przy zerowych warunkach początkowych. G(s) = y(s)/u(s). Transmitancja operatorowa charakteryzuje własności dynamiczne rozpatrywanego elementu liniowego. G(s) = L(s)/M(s) - zatem transmitancja operatorowa jest funkcją wymierną zmiennej zespolonej s. Pierwiastki równania M(s) nazywane są biegunami transmitancji operatorowej, a pierwiastki L(s) = 0 jej zerami.

2.3. Jak przenosi się węzeł sumacyjny?

Jeżeli przenosimy sumator z wejścia elementu na jego wyjście to należy do przenoszonej gałęzi włączyć dodatkowy element o transmitancji X(s) = G(s). Jeżeli natomiast przenosimy z wyjścia elementu na jego wejście to należy do przenoszonej gałęzi włączyć dodatkowy element o transmitancji X(s)=1/G(s).

4.5. Podać transmitancję wypadkową układu zamkniętego ze sprzężeniem zwrotnym w postaci ogólnej.

Jeżeli mamy układ z ± sprzężeniem to transmitancja wypadkowa jest następująca:

6. Co oznacza w kryterium Hurwitza D_n=0 ?

Jeżeli jest spełniony warunek konieczny i wystarczający żeby liniowy układ stacjonarny, ciągły był stabilny asymptotycznie oraz żeby wszystkie podwyznaczniki główne
dla i=1,2..n wyznacznika Hurwitza
były dodatnie. Jeżeli
, oznacza to, że na podstawie tego kryterium nie jesteśmy w stanie stwierdzić nic na temat stabilności układu.

7. Omówić sposób postępowania w przypadku wiersza zerowego w tablicy Routha.

Wiersz leżący bezpośrednio nad nim podaje współczynnik czynnika parzystego

6s⁴ + s² + 5 aby obliczyć poniższe współczynniki tablicy Routha należy obliczyć pochodną czynnika parzystego i współczynniki w tej pochodnej wstawić do tablicy.

8. Omówić sposób postępowania w przypadku elementu zerowego w tablicy Routha

W przypadku kiedy występuje element zerowy w tablicy, to zamiast tego elementu wstawiamy ε, gdyż jest to bardzo mała wartość i kontynuujemy proces obliczeniowy, natomiast pod koniec rozpatrujemy dwa przypadki kiedy ε<0 i ε>0 i dla obu tych przypadków powinna wyjść ta sama ilość zmian znaków czyli ta sama ilość pierwiastków niestabilnych.

9. Podać kryt. Michajłowa  i narysować przebieg M(jω) dla układu na granicy stabilności.

Układ automatycznej regulacji (UAR) jest stabiny jeżeli przyrost argumentu wyrażenia M(jω) (wielomianu Michajłowa) przy zmianach pulsacji od -∞ do +∞ jest rowny n∙π, czyli ∆argM(jω)= n∙π i ω€(-∞,+∞) Przebieg M(jω) dla układu na granicy stabilności - M(jω)= U(ω)+jV(ω)

10. Podać kryt. Michajłowa i jego interpretację na podstawie przebiegu charakterystyk Re{M(jω)} i Im{M(jω)}.

UAR jest stabilny, jeżeli przy zmianach pulsacji od 0 do ∞ charakterystyka M(jω) będzie przechodziła przez n ćwiartek płaszczyzny w dodatnim kierunku trygonometrycznym.

11. Podać postać kryterium Nyquista dla układów astatycznych.

Jeżeli transmitancja G(s) ukł otwartego ma u biegunów = 0 (u>1) a pozostałe jej bieguny znajdują się w lewej półpłaszczyźnie, to ukł po zamknięciu jest stabilny, jeżeli charakterystyka M(jω) uzupełniona łukiem o dużym promieniu R→∞ zaczynając od + półosi rzeczywistej, ukł. Otwartego nie obejmuje punkt (-1;j0)

Kryterium Nyquista:

Układ astatyczny pierwszego rzędu. Charakterystyka w otoczeniu s = 0.

12. Wyjaśnić pojęcie zapasu stabilności amplitudy za pomocą charakterystyk logarytmicznych.

Zapas stabilności amplitudy powoduje, że przy pewnych zmianach parametrów układ nadal jest stabilny. Warunek zapasu stabilności dla charakterystyk logarytmicznych:

13. Podać kryt. Nyquista dla niestabilnego układu otwartego (wariant z przyrostem argumentu).

Równanie charakterystyczne układu zamkniętego ma wszystkie pierwiastki w LPP zmiennej zespolonej s przy założeniu, że równanie układu otwartego ma m pierwiastków w PPP wtedy i tylko wtedy, gdy przyrost argumentu wyrażenia 1+G0(jω) przy zmianach ω od -∞ do +∞ wynosi 2πm, czyli:

14. Podać kryterium Nyquista dla stabilnego układu otwartego (wariant z przyrostem argumentu).

Równanie charakterystyczne układu zamkniętego ma wszystkie pierwiastki w LPP zmiennej zespolonej s przy założeniu, że równanie układu otwartego ma wszystkie pierwiastki w LPP wtedy i tylko wtedy, gdy przyrost argumentu wyrażenia 1+G0(jω) przy zmianach ω od -∞ do +∞ wynosi 0, czyli: (stab. Układ otwarty)

15. Podać kryt. Nyquista dla stabilnego układu otwartego (wariant z charakterystyką amplitudowo-fazową).

Jeżeli układ otwarty jest stabilny:

a) a jego charakterystyka amplitudowo - fazowa nie obejmuje punktu (-1;j0) przy zmianie
to układ zamknięty jest stabilny.

b) a jego charakterystyka amplitudowo - fazowa przechodzi przez punkt (-1;j0) to układ zamknięty znajduje się na granicy stabilności.

16. Podać kryt. Nyquista dla stabilnego układu otwartego (wariant z charakterystykami logarytmicznymi).

Jeśli układ otwarty jest stabilny, a jego charakterystyka amplitudowo - logarytmiczna G₀(jω) ma wszystkie punkty przecięcia z osią P(ω) na prawo od punktu (-1;j0), wtedy i tylko wtedy, gdy dla wszystkich pulsacji ω∈(0;+∞), dla których

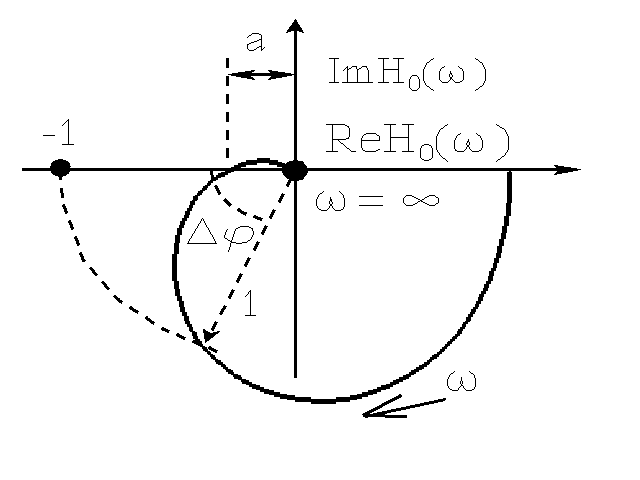
17. Wyjaśnić pojęcie zapasu stabilności amplitudy i fazy za pomocą charakterystyk amplitudowo-fazowych.

Zapas amplitudy określa wartość ϕ, która może być, zwiększona amplitudą układu otwartego, aby układ zamknięty znalazł się na granicy stabilności. Zapas fazowy określa zakres zmian argumentu transmitancji układu otwartego przy stałym wzmocnieniu, która spowodowałaby, że układ zamknięty znalazłby się na granicy stabilności ( zapas faz podawany jest w stopniach lub radianach). Zapasem amplitudy nazywa się wartość 20log₁₀(1/a) wyrażana w dB. Zapasem fazy nazywa się kąt Δϕ.

18->12.

19. Wymienić rodzaje kryteriów jakości UAR.

a) ocena parametrów odpowiedzi skokowej

b) kryteria całkowe

c) kryteria częstotliwościowe (Michajłowa, Nyquista)

d) kryteria rozkładu pierwiastków (Hurwitza Routha)

20. Uzasadnić twierdzenie, że wzrost współczynnika wzmocnienia układu otwartego poprawia jakość w stanie ustalonym.

Wzrost współczynnika wzmocnienia układu otwartego poprawia jakość w stanie ustalonym w sposób uniwersalny, ale prowadzi do utraty stabilności.

Ze wzrostem współczynnika. K maleje uchybienie w stanie ustalonym.

21. Dlaczego podnoszenie stopnia astatyzmu zwiększa dokładność w stanie ustalonym?

Podnoszenie stopnia astatyzmu układ zmniejsza wartość uchyłu ustalonego do wartości zerowej. Jeżeli rząd astatyzmu jest o jeden większy od stopnia wielomianu określającego sygnał wejściowy w funkcji czasu, to uchył regulacji w stanie ustalonym jest równy zero.

I

t→∞

22. Wyznaczyć trzy pierwsze współczynniki uchybu dla układu astatycznego drugiego rzędu.

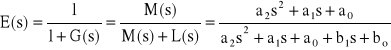
24. Wymienić sposoby poprawiania jakości UAR w stanie ustalonym.

1. wstawienie układu o większym współczynniku wzmocnienia k (zmniejszenie uchybu)

2. zwiększenie rzędu astatyzmu

3. sterowanie z uwzględnieniem pochodnych uchybu

25. Omówić sposób poprawiania jakości układu przez podnoszenie stopnia astatyzmu.iiii Uzasadnić wniosek, że podnoszenie rzędu astatyzmu może spowodować niestabilność. Jaka to niestabilność?

Zwiększenie rzędu astatyzmu (zbyt duże) doprowadzi do niestabilności układu. Ma ona charakter strukturalny ( nie da się ustabilizować bez zmiany struktury układu). Rząd astatyzmu zwiększa się przez dołączenie do układu odpowiedniego członu PI.

26. Wymienić sposób poprawiania jakości UAR za pomocą sterowania z użyciem pochodnych uchybu.

Wprowadzamy człon różniczkujący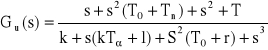

G₂ = 0 to układ miał więcej stabilnych

27. Uzasadnić wniosek, że podnoszenie rzędu astatyzmu może spowodować niestabilność. Jaka to niestabilność?

Jest to niestabilność strukturalna przy układzie otwartym o transmitacji:

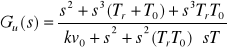
dokładność wzrasta ale układ jest niestabilny, ponieważ przy s nie ma współczynnika. Brak współczynnika wymaga zmiany struktury układu aby osiągnąć stabilność.

28. Wyjaśnić na przykładzie pojęcie niestabilności strukturalnej.

Układ jest niestabilny strukturalnie jeśli żadne zmiany parametrów tego układu nie zapewniają jego stabilności. (co najmniej 1 ze współczynników wielomianu charakterystycznego jest równy zero)

29. Wyjaśnić pojęcie współczynnika oscylacji. Co to jest współczynnik oscylacji?

ω_p - pulsacja rezonansowa; dla której moduł transmitancji widmowej układu zamkniętego G(jω) osiąga wartość maksymalną ( moduł rezonansowy - współcz. oscylacji M_p)

- jest miarą zapasu stabilności układu.

30. Podać przykład transmitancji układu astatycznego II rzędu.

31. Co to jest oscylacyjność?

Jest to tangens największego z kątów odchyleń ψ zespolonych pierw. wieloman. char. od pół osi ujemnej.

32. Co to jest układ astatyczny?

Jest to układ z bezpośrednim sprzężeniem zwrotnym, jeśli transmitancja wypadkowa toru głównego ma bieguny zerowe. Liczba biegunów → rząd astatyzmu

34. Do czego służą okręgi stałej amplitudy?

służą do wyznaczania transmitancji ukł. Zamkniętego,a także współczynnika oscylacji i pulsacji

-srodek okregu:
- promień okręgu R=

35. Podać transmitancję i narysować charakterystyki logarytmiczne korektora przyspieszającego fazę.

36. Podać transmitancję i odpowiedź korektora opóźniającego fazę. Narysować ten przebieg. h(t)

k - wsp. wzmocnienia k -----------

T₀ - czas opóźnienia

T₀

37. Wyjaśnić pojęcie stopnia stabilności.

Stopień stabilności jest definiowany jako:

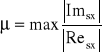
Stopień stabilności mówi nam o szybkości wnikania składowej przebiegu.

38. Narysować charakterystyki logarytmiczne regulatora PD.

39.Narysować charakterystyki logarytmiczne regulatora PID.

40. Narysować charakterystyki logarytmiczne regulatora PI.

41.Narysować h(t) regulatora PI.

Odpowiedź jednostkowa regulatora PI:

42.Wyjaśnić znaczenie stałej T_d regulatora PD za pomocą odpowiedniego rysunku.

odpowiedź:

Czas, o który część różniczkująca k_pT_D wyprzedza część proporcjonalną k_p nazywamy czasem T_D.

43. Wyjaśnić znaczenie stałej T_i regulatora PI za pomocą odpowiedniego rysunku.

Czas zdwojenia T_i - to czas, po którym przebieg osiagnie wartość 2k_p

44. Wymienić podstawowe rodzaje regulatorów.

I - całkujący

P - proporcjonalny

PI - proporcjonalno - całkujący

PD - proporcjonalny - różniczkujący

PID - proporcjonalno - różniczkująco - całkujący

45. Wymienić rodzaje korektorów z punktu widzenia ich właściwości dynamicznych.

• opóźniające fazę

• przyspieszające fazę

• opóźniająco - przyspieszające fazę

46. Wymienić rodzaje korektorów z punktu widzenia ich położenia w układzie.

• szeregowe

• równoległe

• ze sprzężeniem zwrotnym

47. Podać wzór na transformatę splotu funkcji.

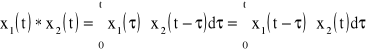
48. Podać wzór na przekształcenie odwrotne transformaty Laplace'a dla pierwiastków pojedynczych równania charakterystycznego.

s_i - pierwiastek funkcji F(s)

49. Podać wzór na przekształcenie odwrotne transformaty Laplace'a dla pierwiastków wielokrotnych równania charakterystycznego.

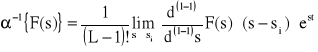
50. Podać wzór na transformatę funkcji e^-αt1(t)

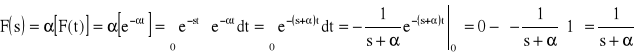
51. Transmitancja wypadkowa połączenia równoległego elementów.

52. Podać wzór na transformatę Laplace'a funkcji t⋅1(t)

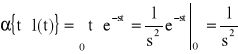
53. Podać wzór na transformatę Laplace'a funkcji te ^-at1(t)

54. Omówić sposób przenoszenia węzła sumacyjnego sprzed bloku za blok.→ 3

55. Jak wyznaczyć odpowiedź układu na dowolny sygnał mając odpowiedź g(t)?

g(t) - transformata odwrotna odpowiedzi impulsowej

g(t) = α^-1{g(s)} ⇒ g(s) = α{g(t)} g(s) = G(s)

56)Podać przykład elementu całkującego rzeczywistego i jego transmitancje.

El. całkujący pierwszego rzędu - czwórnik RC

57) Podać przykład elementu oscylacyjnego i jego transmitancje.

El. oscylacyjny-czwórnik RLC

58.Element różniczkujący rzeczywisty:

przykład: czwórnik RC:

, T=RC

59. Równanie i transmitancja elementu całkującego rzeczywistego.

k - współcz. wzmocnienia

τ - stała czasowa

60. Równanie i transmitancja elementu oscylacyjnego.

ω₀ - pulsacja drgań nietłumionych

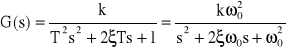
σ - wzgl. współcz. tłumienia

k - współcz. wzmocnienia

61. Równanie i transmitancja elementu różniczkującego rzeczywistego.

62.Przykładowa char. Amplitudowo-fazowa na płaszczyźnie Black'a

element różniczkujący z inercją-

63.Wzór na odpowiedź impulsową elementu całkującego rzeczywistego w funkcji czasu:

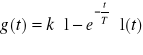
64.Wz. na odp. imp. el. oscylacyjnego w f. Czasu:

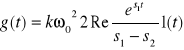
65.Wz. na odp. imp. El. Inercyjnego II rzędu w f. Czasu

66. Wzór na odpowiedź jednostkową elementu oscylacyjnego.

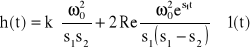
67. Wzór na odpowiedź jednostkową elementu różniczkującego rzeczywistego.

68. Wzór na odpowiedź jednostkową elementu całkującegorzeczywistego w funkcji czasu. Narysować przebieg.

69. Podać równanie i transmitancję elementu inercyjnego drugiego rzędu.

70=73. Postać wykładnicza transmitancji widmowej elem. całkującego rzeczywistego. Przebieg charakterystyki amplitudowo-fazowej.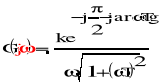

71. Postać wykładnicza transmitancji widmowej elem. różniczkującego rzeczywistego. Przebieg charakterystyki amplitudowo-fazowej.

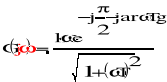
72. Postać wykładnicza transmitancji widmowej elem. inercyjnego II rzędu. Przebieg charakterystyki amplitudowo-fazowej.

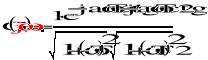
74. Transmitancja widmowej elementu oscylacyjnego. Przebieg charakterystyki amplitudowo-fazowej.

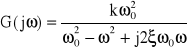
ω - pulsacja rezonansowa.

76. Wzór na odpowiedź jednostkową elementu inercyjnego drugiego rzędu.

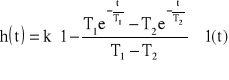
77. Charakterystyki logarytmiczne elementu całkującego rzeczywistego.

78. Charakterystyki logarytmiczne elementu inercyjnego.

79. Charakterystyki logarytmiczne elementu inercyjnego 2 rzędu.

80.Charakterystyki logarytmiczne elementu różniczkującego rzeczywistego

81. Charakterystyki logarytmiczne elementu oscylacyjnego.

82. Charakterystyki logarytmiczne elementu opóźniającego.

83. Wyznaczyć wartość końcową h(t) elementu inercyjnego 2 rzędu za pomocą twierdzeń o wartościach granicznych.

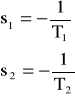
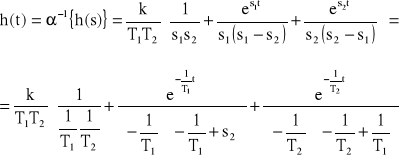
84. Wyznaczyć wartość końcową g(t) elementu całkującego rzeczywistego za pomocą twierdzeń o wartościach granicznych.

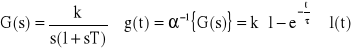
85. Wyznaczyć wartość końcową h(t) elementu różniczkującego rzeczywistego za pomocą twierdzeń o wartościach granicznych,

86. Wyznaczyć wartość początkową h(t) elementu oscylacyjnego za pomocą twierdzeń i wartościach granicznych.

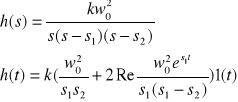
88->91. Sposób wyznaczania liczby pierwiastków równania charakterystycznego w prawej półpłaszczyźnie zmiennej zespolonej s (w PPP) za pomocą kryterium Hurwitza.

Kryterium Hurwitza służy tylko do wyznaczania stabilności bądź niestabilności układu. Ilość zmian znaku argumentów f-cji V decyduje o ilości pierwiastków w PPP, np. jeśli wystąpią 2 zmiany znaku, to oznacza, że istnieją 2 pierwiastki w PPP.

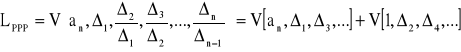
89. Sposób wyznaczania liczby pierwiastków równania charakterystycznego w PPP za pomocą kryterium Michajłowa.

Δarg M(jω) = (n-2m) gdzie n- stopień równ.charakt. m≠0 →ukł.niestabilny

Δarg M(jω) = -π → -π = (3 - 2k)π → -π = 3π -2kπ → k = 2 - dwa pierwiastki w PPP.

90->6

92. Sposób wyznaczania liczby pierwiastków równania charakterystycznego w PPP za pomocą kryt. Routha.

Liczba pierwiastków znajdujących się w PPP jest równa liczbie zmian znaku wyrażeń w pierwszej kolumnie tablicy Routha

94.Podać transmitancję wypadkową układu zamkniętego z dodatnim sprzężeniem zwrotnym w postaci ogólnej.

G(s) = y(s) / u(s) = G₁(s) / (1- G₁(s) G₂(s))

---