Podstawy analizy danych eksperymentalnych
LITERATURA
Guide to the Expression of Uncertainty in Measurement, OSO Switzerland, 1995.
Szczepański W., Kotulski Y. Rachunek błędów. - Warszawa: WN PWN, 1998.
Jaworski B. M., Dietłaf A. A. Fizyka. Poradnik encyklopedyczny. - Warszawa: WN PWN, 1998.
Bronsztejn I. N., Siemienddiajew K. A. Matematyka. Poradnik encyklopedyczny. - Warszawa: WN PWN, 1998.
Wyrażanie niepewności pomiaru. - Warszawa: Główny Urząd Miar, 1999.
Szydłowski H. Pracownia fizyczna. - Warszawa: WN PWN, 1999.
Szydłowski H. Niepewności w pomiarach. - Poznań: WN UAM, 2001.
Kotulski Z., Szczepiński W. Rachunek błędów dla inżynierów. - Warszawa: WNT, 2004.
Korczyński M. Metodyka eksperymentu. - Warszawa: WNT, 2006.
McQuarrie D. A. Matematyka dla przyrodników i inżynierów. Tom 3. - Warszawa: WN PWN, 1998.
TERMINOLOGIA
Pomiarem nazywamy czynności prowadzące do ustalenia wartości wielkości mierzonej.
Pomiarem bezpośrednim nazywamy pomiar wykonany z wykorzystaniem jednego przyrządu pomiarowego.
Pomiarem pośrednim (złożonym) lub wyznaczaniem wielkości nazywamy określenie wielkości poszukiwanej na podstawie wzoru (zależności fizycznej), np. ![]()
, w którym w jakości niezależnych zmiennych występują wielkości, np. ![]()
i ![]()
, mierzone bezpośrednio.
Pomiarem pośrednim (złożonym) nieskorelowanym nazywamy pomiar pośredni, w którym wielkości mierzone bezpośrednio są określane w różnych doświadczeniach.
Pomiarem pośrednim (złożonym) skorelowanym nazywamy pomiar pośredni, w którym wielkości mierzone bezpośrednio są określane w jednym doświadczeniu. Doświadczenia tę mogą być powtarzane wielokrotnie, np. dla określenia ![]()
otrzymamy ciąg par wielkości ![]()
, ![]()
, gdzie ![]()
jest liczbą eksperymentów.
Dobrą ilustracją pomiarów pośrednich (złożonych) skorelowanych są pomiary w obwodach elektrycznych.
Wynikiem pomiaru wielkości mierzonej ![]()
nazywamy wartość (estymator) ![]()
przypisywaną tej wielkości na podstawie eksperymentów. Jest to przybliżenie wartości rzeczywistej, wtedy jak wartość prawdziwa uważa się nie osiąganą na drodze pomiarowej.
Dokładnością pomiaru nazywamy zgodność wyniku pomiaru z wartością rzeczywistą, pojęcie zgodności jest zależne od celą badań.
Powtarzalnością wyników pomiarów nazywamy zgodność ciągu kolejnych wyników pomiarów tej samej wielkości w tych samych warunkach pomiarowych. W zależności od sytuacji określa się warunki powtarzalności.
powtarzalność - stopień zgodności wyników kolejnych pomiarów tej samej wielkości, wykonanych przez tego samego obserwatora, w tych samych warunkach, przy użyciu tych samych narzędzi i metod pomiarowych.
Odtwarzalnością wyników pomiarów nazywamy zgodność ciągu kolejnych wyników pomiarów tej samej wielkości w różnych warunkach pomiarowych. W zależności od sytuacji określa się warunki odtwarzalności lub czynniki nieistotne.
odtwarzalność - stopień zgodności wyników kolejnych pomiarów tej samej wielkości, wykonanych przez różnych obserwatorów, przy użyciu różnych metod pomiarowych, w długich odstępach czasowych.
Niepewności pomiarowe
Nazwa, źródło |
Objawy |
Przyczyny |
Niepewność przypadkowa. Natura zjawiska |
Rozrzut wyników pomiarów wykonanych na elementach jednorodnego zbioru |
Statystyczny charakter zjawiska fizycznego. Brak identyczności elementów zbioru |
Niepewność przypadkowa. Określenie obiektu. |
Rozrzut wyników kolejnych pomiarów tego samego obiektu |
Niezgodność obiektu z przyjętym dla niego modelem |
Niepewność przypadkowa. Czynniki nieistotne
|
Rozrzut wyników pomiarów wykonywanych w różnym czasie, miejscu, przez różne osoby, różnymi przyrządami pomiarowymi... |
Zmienność czynników uznanych za nieistotne. Zmienność reakcji zmysłów |
Niepewność wzorcowania. Stosowane przyrządy lub wzorce. |
Występuje zawsze. Dominuje, gdy nie ma rozrzutu wyników. |
Niepewność pomiarowa stosowanych mierników. Niepewność wzorców stanowiących odniesienie |
Niepewność eksperymentatora. Trudności odczytu. |
Niepewność poprawności wyniku pomiaru |
Zmienia się wskazanie, błąd w układzie pomiarowym |
Niepewność wielkości z literatury |
Brak objawów (występuje tylko w pomiarach pośrednich). |
Niepewność pomiarowa wielkości z literatury lub innego źródła. |
Niepewnością pomiarową nazywamy pewien parametr charakteryzujący rozrzut wyników pomiaru wielkości mierzalnej.
Obliczanie niepewności metodą typu A jest to określenie miary niepewności na podstawie analizy statystycznej serii wyników. Przy tym wykorzystuje się powstałe w rzeczywistości częstości poszczególnych wyników.
Obliczanie niepewności metodą typu B jest to określenie miary niepewności na podstawie analizy statystycznej z wykorzystaniem częstości poszczególnych wyników lub innych hipotez sformułowanych przez badacza.
ZMIENNA LOSOWA
Próbą nazywamy skończony ciąg wyników ![]()
pomiarów wielkości fizycznej ![]()
. Mówi się, że zbiór ![]()
należę do populacji - zbioru wszystkich możliwych wartości, które możemy otrzymać w pomiarze.
Ze względu na wartość liczby ![]()
rozróżniamy próbę:
bardzo małe (![]()
),
małe (![]()
),
duże (![]()
)
bardzo duże (![]()
).
Histogram jest to ilustracja graficzna wyników pomiarów eksperymentalnych wielkości fizycznej ![]()
zbudowana w następujący sposób. Zakres możliwych do uzyskania wyników pomiarów podzielony jest na ![]()
małych przedziałów, zwykłe o jednakowej długości (pozioma oś ![]()
). Nad każdym przedziałem, np. w postaci słupka odpowiedniej długości, określa się liczba ![]()
pomiarów, w których uzyskano wartość badanej wielkości ![]()
(częstości tego wyniku).
1. Miary położenia wyników w tendencji centralnej.
Wartość średnia (arytmetyczna) próby definiuje się wzorem
![]()
. (1.1)
Z wykorzystaniem danych, na których oparty jest histogram, wartość średnia (arytmetyczna) próby może być zapisana w postaci często stosowanej w praktyce
![]()
lub ![]()
, (1.2)
gdzie ![]()
jest liczbą różnych według histogramu wyników pomiaru ![]()
oraz ![]()
.
Należę podkreślić, że wynik obliczeń na podstawie wzoru (1.2) może istotnie zależeć od liczby ![]()
, który wykorzystany dla określenia histogramu.
Wartość średnia (geometryczna) próby definiuje się wzorem
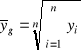
. (1.3)
Wartość średnia (geometryczna) próby często stosuje się, np. w fizyce, dla określenia średniej prędkości zmian zjawisk.
Wartość średnia (harmoniczna) próby definiuje się wzorem
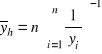
. (1.4)
Wartość średnia (harmoniczna) próby stosuje się w tych przypadkach, kiedy wartości zmiennej podane w jednostkach względnych, np. ![]()
, ![]()
itp., a ich wagi w jednostkach licznika tych jednostek względnych.
Przykład. Mamy stanowisko z sześciu linij, który produkują tabletki jak to podano w poniższej tablice. Jaka średnia wydajność stanowiska?
Linia |
1 |
2 |
3 |
4 |
5 |
6 |
Liczba wyprodukowanych sztuk |
2000 |
2000 |
2000 |
2000 |
2000 |
2000 |
Czas produkcji (min) |
20 |
25 |
20 |
20 |
25 |
10 |
Średnia wydajność linii (szt./min) |
100 |
80 |
100 |
100 |
80 |
200 |
Wartość średnia (harmoniczna)
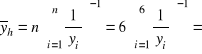
![]()
Wartość średnia (arytmetyczna)
![]()
Można sprawdzić, że ostatni wynik jest błędny, dzieląc łączną liczbę tabletek
![]()
przez łączny czas
![]()
,
otrzymamy wynik ![]()
.
Mediana (wartość środkowa) próby jest to wartość pomiaru środkowego w ciągu uporządkowanych wyników pomiaru taka, że prawdopodobieństwo wystąpienia wyników mniejszych i wyników większych jest równa ![]()
. Dla parzystej liczby pomiarów ![]()
mamy
![]()
(1.5)
wówczas dla nieparzystej liczby
![]()
. (1.6)
Wykorzystanie mediany jest wskazane, kiedy rozkład (histogram) wykazuje silną asymetrię.
Moda (dominanta) jest najczęściej obserwowany wynik pomiarów (![]()
).
2. Miary rozrzutu.
Rozstęp (rozrzut wyników) próby określa się wzorem
![]()
, (1.7)
gdzie ![]()
i ![]()
są największą i najmniejszą wartością zmiennej losowej w próbce.
Rozstęp (rozrzut wyników) próby jest najprostszą miarą rozproszenia wyników pomiarów.
Odchylenie standardowe próby definiowane wyrażeniem
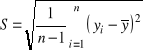
(1.8)
oraz wariancja dla próby
![]()
. (1.9)
Wówczas odchylenie standardowe dla populacji definiowane wyrażeniem
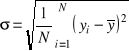
(1.10)
oraz wariancja dla populacji
![]()
. (1.11)
Podkreślimy, że pojęcie populacja określa się jako zbiór wszystkich dopuszczalnych rezultatów pomiarów, wtedy jak próba jest konkretną realizacją ![]()
pomiarów (![]()
).
W praktyce wzór (1.8) stosuje się dla bardzo małej i małej próby, wówczas (1.10) - dla bardzo dużej próby.
Definicja. Mówimy, że miarą niepewności wyniku ![]()
jest odchylenie standardowe ![]()
.
Współczynnik zmienności (Pearsona) próby oznaczamy wzorem
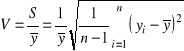
, ![]()
. (1.12)
Współczynnik zmienności (Pearsona) stosowany jest wtedy, kiedy w badaniach eksperymentalnych stosowane są różne jednostki pomiarowe lub należę porównywać wielkości o istotnie różnych wartościach średnich.
Z-nota próby ma postać
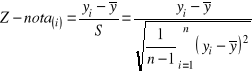
. (1.13)
Z-nota próby jest ważną względną charakterystyką rozproszenia (niepewności) pomiarów.
Odchylenie standardowe średniej określamy wzorem
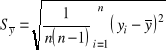
. (1.14)
Łatwo zauważyć, że zachodzi związek
![]()
. (1.15)
Definicja. Niepewnością średniej wyników ![]()
nazywamy odchylenie standardowe średniej ![]()
oraz według [1] niepewnością standartową
![]()
. (1.16)
3. Miary zniekształcenia rozkładów.
W praktyce szeroko stosuje się dwie podstawowe wielkości dla porównania miary zniekształcenia rozkładów
Asymetrię rozkładu dla próbki charakteryzujemy przez parametr
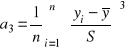
. (1.17)
oraz spłaszczenie rozkładu określamy wyrażeniem
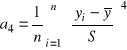
. (1.18)
4. Ocena niepewności metodą typu B.
Jeśli wyniki pomiarów nie wykazują rozrzutu statystycznego, tzn. z przyjętą dokładnością ![]()
, to niepewność standardowa musi być określona w inny sposób.
Niepewnością wzorcowania nazywamy niepewność związaną z dokładnością „wzorca” stosowanego w pomiarach.
Załóżmy, że wynik pomiaru ![]()
, a niepewność wzorcowania ![]()
. Wtedy prawdopodobieństwo ![]()
uzyskania dowolnej wartości mieszczącej się w przedziale
![]()
jest z założenia jednakowe. Mówi się o rozkładzie jednostajnym (rys.).
Definicja. Odchylenie standardowe, a tym samym niepewność standardowa w rozkładzie jednostajnym określa się wzorem
![]()
. (1.19)
Wówczas
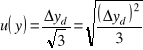
. (1.20)
Jeśli apriori wiadomo o realizacji innych rozkładów, np. trójkątnych (rys), to możemy korzystać z następnej definicji
![]()
. (1.21)
Wówczas
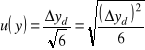
. (1.22)
Niepewnością eksperymentatora nazywamy niepewność wynikającą ze znanych, ale nie zawsze możliwych do usunięcia, przyczyn, np. zaburzeń odczytu danych.
Definicja. Jeśli niepewność odczytu szacuje się jako ![]()
, to niepewność standardową będziemy szacować na podstawie rozkładu jednostajnego
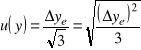
. (1.23)
Niepewnością wielkości pobranej z literatury nazywamy niepewność związaną z danymi literaturowymi:
jeśli podano równocześnie odchylenie standardowe wielkości, to niepewność standardową
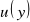
przyjmuje się jej równą;jeśli podano trójkrotne odchylenie standardowe
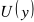
, to niepewność standardową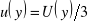
;przy braku dodatkowych informacji przyjmujemy, że niepewność
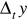
jest równa 10 jednostek miejsca rozwinięcia dziesiętnego o najmniejszej wartości, wtedy
![]()
. (1.24)
5. Błąd pomiaru.
Tradycyjnie błąd pomiaru tłumaczyli zewnętrznym przypadkiem losowym lub błędem systematycznym.
Teraz według [1] należę mówić: błąd pomiaru - niedoskonałość eksperymenty doprowadzająca do wyniku różnego od wartości rzeczywistego.
Tradycyjnie błąd przypadkowy związany jest z nieprzewidywalnymi czynnikami.
Tradycyjnie błąd systematyczny polega nie uwzględnieniu pewnego istotnego czynnika.
Kiedy błąd pomiaru jest większy od niepewności, to wynik jest błędny.
Błędy pomiarowe
Nazwa, źródło |
Objawy |
Przyczyny |
Błąd przeoczenia |
Niezgodność wyniku z wartością uznaną za poprawną |
Działanie czynników niekontrolowanych uznanych za nieistotne |
Pomyłki |
Duże odstępstwo wyniku od wartości poprawnej |
Pomyłka eksperymentatora. Niepoprawna obsługa przyrządu. Przyjęcie błędnych założeń. |
Błąd przybliżenia |
Niezgodność wyniku z wartością uznaną za poprawną |
Uproszczenie warunków pomiaru. Stosowanie przybliżonego wzoru. |
6. Obliczanie i zapis wyników.
Niepewność całkowita. W przypadku rozrzutu statycznego jako wynik końcowy przyjmujemy średnią arytmetyczną ![]()
określoną wzorem (1.1), wówczas przeciwnej sytuacji braku takiego rozrzutu
![]()
. (1.25)
W statystyce matematycznej addytywne są wariancji. Zatem za niepewność całkowitą wyniku ![]()
przyjmujemy
![]()
. (1.26)
Zaokrąglanie wyników i ich zapis.
A. Sprowadzamy wynik pomiaru i jego niepewność do tych samych jednostek, np. układu SI.
B. Zaokrąglanie wyników rozpoczyna się z zaokrąglania niepewności pomiarowej do pierwszego względnie pierwszych dwóch miejsc rozwinięcia dziesiętnego. Oznacza to, że niepewność pomiarowa zapisana w postaci
![]()
, (1.27)
gdzie ![]()
przyjmują wartości ze zbioru ![]()
, a ![]()
jest liczba całkowita.
Wtedy przyjmujemy, że jeśli:
![]()
, to ![]()
; ![]()
, to ![]()
,
gdzie ![]()
są cyfry po zaokrąglaniu.
C. Wynik pomiaru zaokrąglamy na tym samym miejscu rozwinięcia dziesiętnego co niepewność.
D. Reguły zaokrąglania:
cyfry 0-4 zaokrąglamy w dół, tzn. nie zmieniamy cyfry poprzedzającej, np. ![]()
lub ![]()
;
cyfry 5-9 zaokrąglamy w górę, tzn. podwyższamy cyfrę poprzedzającą o jeden, np. ![]()
lub ![]()
;
E. Zapis wyniku.
Mamy (opór przewodnika)
![]()
, ![]()
, ![]()
.
Krok pierwszy
![]()
, ![]()
, ![]()
.
Krok drugi
![]()
(![]()
, więc zaokrąglenie do jednego miejsca).
Krok trzeci
![]()
, ![]()
, ![]()
.
Mamy (przyspieszenie ciała)
![]()
, ![]()
, ![]()
.
Krok pierwszy
![]()
, ![]()
, ![]()
.
Krok drugi
![]()
(![]()
, więc zaokrąglenie do dwóch miejsc).
Krok trzeci
![]()
, ![]()
, ![]()
.
Mamy (pojemność kondensatora)
![]()
, ![]()
, ![]()
.
Krok pierwszy
![]()
, ![]()
, ![]()
.
Krok drugi
![]()
(![]()
, więc zaokrąglenie do jednego miejsca).
Krok trzeci
![]()
, ![]()
, ![]()
.
Mamy (ważenie ciała)
![]()
, ![]()
, ![]()
.
Krok pierwszy
![]()
, ![]()
, ![]()
.
W tym miejscu należę obliczyć niepewność na podstawie założenia o jednostajnym rozkładzie wartości pomiaru w przedziale ![]()
![]()
.
Wówczas krok pierwszy ostatecznie
![]()
, ![]()
, ![]()
.
Krok drugi
![]()
(![]()
, więc zaokrąglenie do dwóch miejsc).
Krok trzeci
![]()
, ![]()
, ![]()
.
Wytyczne do składania protokółu wymienione w [1, 2].
Niepewności w pomiarach bezpośrednich.
A. Pomiary próbne i wstępna ocena.
Określamy niepewność wzorcowania ![]()
, np. przez wartość działki elementarnej przyrządu dla pomiarów.
Wykonujemy serie około 10 pomiarów próbnych.
Dokonujemy oceny rozstępu ![]()
.
Przyjmuje się, że można dokonywać dalszych pomiarów jeżeli ![]()
.
Jeśli nierówność była spełniona, to dokonujemy kolejnych około 100 pomiarów.
B. Dobór przedziałów klasowych.
Określamy przedział zmienności jako rozstęp z nadmiarem.
Przedział zmienności dzielimy na liczbę ![]()
(zwykłe 6-10) dla otrzymania przedziałów klasowych o równej długości prawostronnie domkniętych. Pożądane jest, żeby długość przedziałów klasowych była wielokrotnością działki elementarnej stosowanego przyrządu.
Dokonujemy sortowania próby i budujemy tabele, np. o następującej postaci, gdzie ![]()
oznacza numer przedziału klasowego, a ![]()
wartość średnia w tym przedziale.
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
|
|
|
|
|
|
|
….. |
….. |
….. |
…. |
….. |
…… |
……. |
……. |
………. |
|
|
|
|
|
|
|
|
|
C. Histogram i wielobok częstości.
D. Średnia i odchylenie średniej wyników poklasowach.
Stosuje się wzory
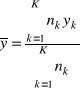
dla średniej,
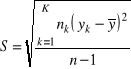
dla odchylenia standardowego oraz
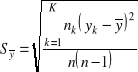
dla odchylenia standardowego średniej.
Pomiary bezpośrednie i ich wyniki.
Pomiary próbne o liczbie 3-5 wykorzystujemy, żeby wyciągnąć następujące wnioski:
czy można pominąć niepewność eksperymentatora, tzn.
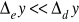
;czy są wyniki znacznie różniące się od pozostałych i czy jest wynik grubego błędu;
sprawdzamy czy występują wyniki identyczne, czy raczej statystyczne, i ostatnim przypadky przyjmujemy, że niepewność standartowa jest równa połowie rozstępu.
Pomiary uzupełniające o liczbie od 5-10 wykonuje się jeśli próbne nie dają możliwości wyciągnięcia pożądanych wymienionych powyżej wniosków.
Pomiary dodatkowe określamy na podstawie pomiarów próbnych i uzupełniających. Jeżeli:
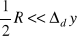
, tzn. dominuje niepewność wzorcowania, to nalezę zmodyfikować stanowisko pomiarowe, wyniki szacuje się na podstawie pomiarów próbnych i uzupełniających;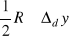
, to też nalezę zmodyfikować stanowisko pomiarowe, wyniki szacuje się na podstawie pomiarów próbnych i uzupełniających;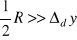
, tzn. dominuje niepewność przypadkowa, to nalezę przeprowadzić dodatkowe pomiary dla zmniejszenia niepewności.
Liczbę dodatkowych pomiarów określamy na podstawie pomiarów próbnych i uzupełniających ze wzorów
![]()
lub ![]()
, (1.28)
gdzie ![]()
jest wartość krytyczna zmiennej ![]()
-Studenta dla próby z ![]()
pomiarów i poziomem ufności (istotności) ![]()
(![]()
), a ![]()
jest z góry założonej dokładnością.
Dla realizacji tego plany na podstawie ![]()
pomiarów postępujemy tak:
obliczamy
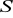
lub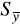
;zakładamy dokładność pomiaru
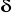
(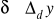
);przyjmujemy poziom istotności
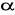
(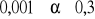
);z tabeli odczytujemy wartość krytyczna zmiennej
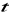
-Studenta;obliczamy liczby
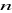
ze wzoru (1.28) z zaokrąglaniem w górę do najbliższej liczby całkowitej.
Wartości krytyczne ![]()
rozkładu Studenta
|
|
|
|
|
2 |
6,3138 |
12,7062 |
31,8205 |
127,3213 |
3 |
2,9200 |
4,3027 |
6,9646 |
14,0890 |
4 |
2,3534 |
3,1824 |
4,5407 |
7,4533 |
5 |
2,1318 |
2,7764 |
3,7469 |
5,5976 |
6 |
2,0150 |
2,5706 |
3,3649 |
4,7733 |
7 |
1,9432 |
2,4469 |
3,1427 |
4,3168 |
8 |
1,8946 |
2,3646 |
2,9980 |
4,0293 |
9 |
1,8595 |
2,3060 |
2,8965 |
3,8325 |
10 |
1,8331 |
2,2622 |
2,8214 |
3,6897 |
15 |
1,7613 |
2,1448 |
2,6245 |
3,3257 |
20 |
1,7291 |
2,0930 |
2,5395 |
3,1737 |
25 |
1,7109 |
2,0639 |
2,4922 |
3,0905 |
OBLICZANIE NIEPEWNOŚCI POMIARÓW POŚREDNICH
Obliczanie średnich i odchyleń standartowych dla pomiarów pośrednich w przypadku dwóch niezależnych wielkości.
Załóżmy, że pewna wielkość oblicza się ze wzoru
![]()
, (1.29)
gdzie ![]()
i ![]()
— wielkości fizyczne mierzone bezpośrednio.
Próbki ![]()
i ![]()
pozwalają obliczyć średnie
![]()
i ![]()
. (1.30)
Dla uproszczenia zapisu oznaczmy odchylenie wielkości mierzonych od ich wartości średnich przez
![]()
i ![]()
. (1.31)
Wtedy odchylenie standardowe średniej w każdej z rozważanych próbek zapiszemy w postaci
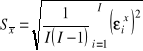
i 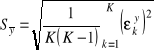
. (1.32)
Wartości wielkości fizycznych mierzonych pośrednio możemy obliczyć ze wzoru (1.29), tzn. ![]()
, lub stosując oznaczenia (1.31) notujemy
![]()
. (1.33)
Dokonamy rozwinięcia w szereg Taylor'a w otoczeniu punktu ![]()
i zaniedbamy składniki wyższych rzędów (liniowe przybliżenie)
![]()
, (1.34)
gdzie ![]()
i ![]()
— pochodne cząstkowe względem pierwszego i drugiego argumentu w punkcie ![]()
.
Twierdzenie. Wartość średnia dla próbki wielkości fizycznej ![]()
określa się ze wzoru
![]()
. (1.35)
Udowodnienie. Z definicji średniej mamy
![]()
Podstawiamy rozwinięcie (1.34) i dokonamy prostych przekształceń
![]()
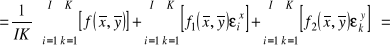
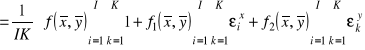
Ponieważ
![]()
,
oraz
![]()
i
![]()
,
to ostatecznie otrzymamy ![]()
.
Twierdzenie. Odchylenie standardowe wielkości ![]()
określa się wzorem
![]()
. (1.36)
Dowód. Dla skrócenia zapisu wykorzystamy wielkości
![]()
.
Uwzględniając (1.34), tzn. ![]()
, dla tych wielkości otrzymamy
![]()
. (1.37)
Zgodnie z definicją średniej zapisujemy
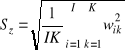
.
Podstawiając wyrażenie (1.37) do definicji średniej dla wariancji wielkości fizycznej ![]()
mamy
![]()
Dokonamy przekształceń. Po podniesieniu do kwadratu zapiszemy
![]()
.
Ponieważ wielkości ![]()
i ![]()
nie zależą od symboli sumowania, to przepisujemy powyższe wyrażenie w postaci
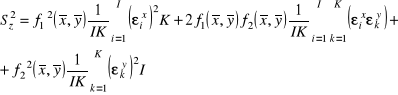
Z tego, że
![]()
,
znajdziemy
![]()
Znowu korzystając z definicji (1.30), tzn.
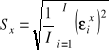
i 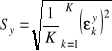
,
i ostatecznie mamy poszukiwany wynik.
Twierdzenie. Podobnie dla odchylenia standardowego średniej wartości ![]()
![]()
,
gdzie ![]()
i ![]()
.
Uogólnienie na przypadek wielu niezależnych zmiennych.
Załóżmy, że pewna wielkość fizyczna określona jest przez następującą funkcjonalną zależność
![]()
. (1.38)
Wtedy w sposób podobny, jak i w przypadku dwóch niezależnych zmiennych, możemy udowodnić, że wartość średnia określa się wzorem
![]()
, (1.39)
a odchylenie standardowe wyrażeniem
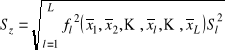
. (1.40)
Przy tym odchylenie standardowe średniej będzie
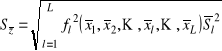
,
gdzie ![]()
I. Ważny przypadek cząstkowy. Załóżmy, że poszukiwana wielkość fizyczna jest określona przez wzór
![]()
. (1.41)
Pochodna tej funkcji można zapisać w postaci
![]()
.
Skąd wartość średnia i odchylenie standartowe będzie
![]()
, 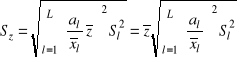
,
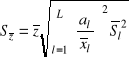
. (1.42)
II. Ważny przypadek cząstkowy. Załóżmy, że poszukiwana wielkość fizyczna jest określona przez wzór
![]()
, (1.43)
gdzie ![]()
— niezależne zmienne losowe (![]()
).
Pochodna tej wielkości
![]()
i ze wzorów (1.39) i (1.40) otrzymamy
![]()
, (1.44)
a odchylenie standardowe wyrażeniem
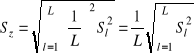
, (1.45)
gdzie odpowiednia wariancja standardowa określona wyrażeniem
![]()
. (1.46)
Jeśli teraz będziemy uważać, że każda niezależne zmienna losowa ![]()
(![]()
) jest ![]()
elementową próbą pomiarów tej samej wielkości fizycznej, to ze wzorów (1.44) - (1.46) znajdziemy
![]()
,
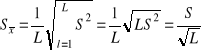
,
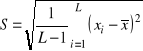
.
Łącząc ostatni dwa wyrażenia, otrzymamy
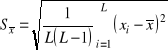
.
Innymi słowami, jeśli w jakości funkcji ![]()
wybieramy wartość średnią
![]()
,
to udowodnimy wzór (1.14) dla odchylenia standardowego średniej.
Obliczanie niepewności maksymalnych
Niech mamy zależność
![]()
. (1.47)
W wyniku eksperymentu uzyskano wartości
![]()
oraz ich niepewności
![]()
.
Wtedy w miejsce wyrażenia (1.47) zapiszemy
![]()
Dokonamy rozwinięcia w szereg Taylor'a
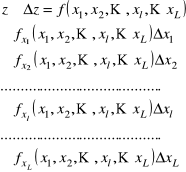
Skąd dla niepewności funkcji ![]()
znajdziemy
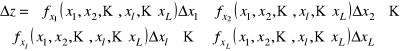
albo w skrócie
![]()
.
Definicja. Za niepewność maksymalną przyjmiemy
![]()
. (1.48)
W przypadku kiedy
![]()
, mamy ![]()
.
Losowa metoda oceny niepewności rozszerzonych.
Niepewnością rozszerzoną nazywamy odchylenie standardowe pomnożone przez stałą.
Równanie
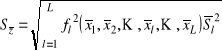
,
gdzie ![]()
, mnożymy przez 3
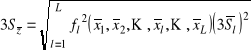
Wykorzystujemy
![]()
i ![]()
otrzymujemy
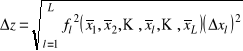
albo
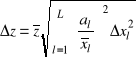
Rozkład normalny
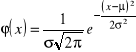
Postać standaryzowana rozkładu normalnego
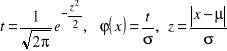
Całka Laplace'a
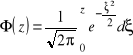
Prawdopodobieństwo, że ![]()
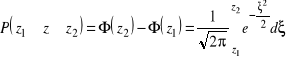
Dla ![]()
, więc możemy przyjąć, że rozstęp ![]()
.
Zmienna losowa ![]()
dla rozkładu normalnego
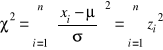
Rozkład zmiennej losowej ![]()
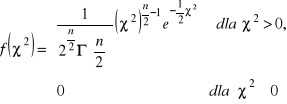
Całka Euler'a
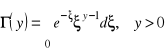
lub
![]()
Rozkład t-Studenta
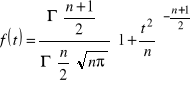
, ![]()
Rozkład F (Fishera - Snedecora)
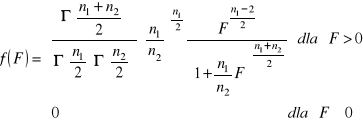
, 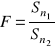
![]()
![]()
65,0%
![]()
![]()
![]()
![]()
![]()
57,7%
![]()
![]()
![]()
![]()
![]()
![]()
![]()
57,7%
![]()
![]()
![]()
![]()
Wyszukiwarka