1. Wyprowadzić wzór na prędkość punktu ciała sztywnego poruszającego się ruchem płaskim.

Prędkość dowolnego punktu B figury płaskiej, poruszającej się w swej płaszczyźnie , równa jest sumie geometrycznej prędkości dowolnie obranego punktu A tej figury , zwanego biegunem, oraz prędkości punktu B względem bieguna A, czyli prędkości punktu B w ruchu obrotowym figury wokół bieguna. Prędkość kątowa tego ruchu obrotowego nie zależy przy tym od wyboru bieguna A.

Aby obliczyć tą prędkość wykorzystamy wzór:

Gdy początek układu ruchomego przyjmiemy w punkcie A, a wektor o początku w punkcie A i końcu w punkcie B oznaczamy jako AB=r_AB to na podstawie powyższego wzoru prędkość punktu B bryły możemy wyznaczyć:

Zatem:

Ze względu na to ,że wektor prędkości punktu B względem A jest prostopadły do r_AB moduł obliczamy ze wzoru:

2. Wyprowadzić wzór na przyspieszenie punktu ciała sztywnego w ruchu płaskim.

Skorzystamy ze wzoru:

Ze względu na to , że ωr΄=0 powyższy wzór uprości się do:

Na podstawie tego wzoru przyśpieszenie punktu B możemy zapisać następująco:

albo

Przyśpieszenie a_BA jest spowodowane chwilowym obrotem bryły wokół bieguna:

Z powyższego wzoru wynika, że przyśpieszenie to możemy rozłożyć na składowe:

gdzie:

Moduły tych przyśpieszeń są następujące:

Przyśpieszenie punktu B można ostatecznie zapisać:

3. Omówić metody wyznaczania prędkości punktów ciała sztywnego w ruchu płaskim.

1. Prędkość dowolnego punktu B figury płaskiej, poruszającej się w swej płaszczyźnie , równa jest sumie geometrycznej prędkości dowolnie obranego punktu A tej figury , zwanego biegunem, oraz prędkości punktu B względem bieguna A, czyli prędkości punktu B w ruchu obrotowym figury wokół bieguna. Prędkość kątowa tego ruchu obrotowego nie zależy przy tym od wyboru bieguna A.

Aby obliczyć tą prędkość wykorzystamy wzór:

Gdy początek układu ruchomego przyjmiemy w punkcie A, a wektor o początku w punkcie A i końcu w punkcie B oznaczamy jako AB=r_AB to na podstawie powyższego wzoru prędkość punktu B bryły możemy wyznaczyć:

Zatem:

Ze względu na to ,że wektor prędkości punktu B względem A jest prostopadły do r_AB moduł obliczamy ze wzoru:

2. Kolejna metoda to wyznaczenie prędkości gdy mamy dany chwilowy środek obrotu. Możemy wtedy obliczyć prędkość dowolnego punktu M bryły. Jeżeli biegun redukcji przyjmiemy w chwilowym środku obrotu C , a nie w dowolnym punkcie O', to prędkość dowolnego punktu M bryły można wyrazić wzorem:

V=V_C+ ω×CM

Ponieważ z założenia prędkość punktu C jest równa zeru więc prędkość punktu M będzie opisana wzorem:

V= ω×CM

Z otrzymanego wzoru wynika , że prędkość dowolnego punktu M bryły jest prostopadła do prostej łączącej punkt M z chwilowym środkiem obrotu C. ponadto wektory ω i CM są prostopadłe więc moduł prędkości:

V= ωCM

4. Co to jest chwilowy środek obrotu i jak go znajdujemy?

Jeżeli figura płaska porusza się w swej płaszczyźnie, to z każdego położenia w inne położenie daje się przesunąć przez obrót dokoła punktu leżącego w tej płaszczyźnie, zwanego środkiem obrotu skończonego (przesunięcie równolegle można uważać za obrót punktu leżącego w nieskończoności).

Rys.19.2

Jeżeli figura płaska w chwili t₀ zajmuje położenie I, a w chwili t₁ położenie II (rys. 19.2) to można wyznaczyć środek skończonego obrotu. Jeżeli bierzemy coraz bliższe położenie, tak że t₁
t_o , to dla każdego z tych położeń można wyznaczyć środek skończonego obrotu. Dla coraz bliższych położeń, położenie środka skończonego obrotu zmierza do pewnego położenia granicznego. Graniczne położenie środka skończonego obrotu, gdy t₁
t₀ , nazywamy chwilowym środkiem obrotu w chwili t₀.

WYZNACZANIE: Znane są kierunki prędkości
dwóch punktów A i B płaskiej figury. Chwilowy środek obrotu znajdujemy na przecięciu się prostych prostopadłych, poprowadzonych z punktów A i B, do kierunków prędkości 
tych punktów (rys 19.4).

5. Jakie są cechy jednostajnego i jednostajnie zmiennego (przyspieszonego i opóźnionego) ruchu punktu?

ęłęóCechy ruchu jednostajnego prostoliniowego: kierunek i zwrot wektora prędkości jest stały i zgodny z kierunkiem i zwrotem ruchu, - wartość prędkości jest stała, - prędkość średnia równa jest prędkości chwilowej, - przyspieszenie jest równe zeru, ponieważ wektor prędkości jest stały (zmiana prędkości wynosi 0). Zgodnie z I zasadą dynamiki, do tego żeby ciało poruszało się ruchem jednostajnym prostoliniowym, nie jest potrzebna żadna siła.

Cechy ruchu jednostajnie przyspieszonego(opóźnionego): kierunek i zwrot prędkości jest stały i zgodny z kierunkiem i zwrotem ruchu, wartość prędkości nie jest stała-stała jest wartość przyśpieszenia- ponieważ wartość prędkości rośnie o taką samą wartość w takich samych odstępach czasu. Zgodnie z drugą zasadą dynamiki przyspieszenie jest wprost proporcjonalne do działającej siły i odwrotnie proporcjonalne do masy. Ruch jednostajnie opóźniony ma te same cechy z tym, że w takich samych odstępach czasu prędkość maleje o tę samą wartość.

Ruch prostoliniowy jednostajnie zmienny (przyspieszony lub opóźniony):
(przyspieszenie jest stałe).

Rozważamy ruch ciała, które w chwili początkowej
znajdowało się w położeniu
i miało prędkość

Jeśli w chwili początkowej ciało znajdowało się w początku układu współrzędnych
, wówczas:

Otrzymaliśmy w ten sposób znany ze szkoły wzory na prędkość i przemieszczenie ciała w ruchu jednostajnie zmiennym.

Charakterystyczne cechy ruchu jednostajnie zmiennego:

• zależność prędkości ciała od czasu jest liniowa

• zależność położenia od czasu jest parabolą

• w takich samych odstępach czasu ciało przebywa coraz większe (ruch przyspieszony) lub coraz mniejsze (ruch opóźniony) odcinki drogi.

• Określić pochodną wektora zmiennego.

6. Omówić istotę tarcia tocznego.

Załóżmy, że sztywny walec o ciężarze G spoczywa na sztywnej poziomej płaszczyźnie. Do walca przyłożymy poziomą siłę P odległa od płaszczyzny o h. przy założeniu sztywności walca i płaszczyzny będzie się on tykał wzdłuż tworzącej przechodzącej przez punkt A. W tym punkcie wystąpi reakcja podłoża, którą rozłożono na normalną N i styczną T. Jeżeli walec znajduje się w spoczynku, to siły działające na niego muszą być w równowadze tzn. ich suma geometryczna musi być równa zeru. T=P G=N

Założymy , że siła P jest mniejsza od granicznej wartości siły tarcia: P≤μN

Oznacza to, że walec nie może się ślizgać po płaszczyźnie. Z analizy układu wynika , że nie może być on też w ównowadze. Łatwo zauważyć , że dla każdej wartości siły P różnej od zera i h różnego od zera siła ta daje moment względem punktu A, którego wartość jest różna od zera. W tej sytuacji najmniejsza wartość siły P spowodowałaby obrót walca co jest sprzeczne z zachowaniem się ciał rzeczywistych w podobnej sytuacji. W rzeczywistości jeżeli walec i podłoże są wykonane z rzeczywistych materiałów, to przy małej wartości siły P toczenie walca nie wystąpi. Zacznie się on toczyć dopiero po przekroczeniu przez moment siły P względem punktu A pewnej wartości charakterystycznej dla materiałów walca i podłoża.

7. Omówić metody wyznaczania prędkości punktów ciała sztywnego w ruchu płaskim.

3. Prędkość dowolnego punktu B figury płaskiej, poruszającej się w swej płaszczyźnie , równa jest sumie geometrycznej prędkości dowolnie obranego punktu A tej figury , zwanego biegunem, oraz prędkości punktu B względem bieguna A, czyli prędkości punktu B w ruchu obrotowym figury wokół bieguna. Prędkość kątowa tego ruchu obrotowego nie zależy przy tym od wyboru bieguna A.

Aby obliczyć tą prędkość wykorzystamy wzór:

Gdy początek układu ruchomego przyjmiemy w punkcie A, a wektor o początku w punkcie A i końcu w punkcie B oznaczamy jako AB=r_AB to na podstawie powyższego wzoru prędkość punktu B bryły możemy wyznaczyć:

Zatem:

Ze względu na to ,że wektor prędkości punktu B względem A jest prostopadły do r_AB moduł obliczamy ze wzoru:

4. Kolejna metoda to wyznaczenie prędkości gdy mamy dany chwilowy środek obrotu. Możemy wtedy obliczyć prędkość dowolnego punktu M bryły. Jeżeli biegun redukcji przyjmiemy w chwilowym środku obrotu C , a nie w dowolnym punkcie O', to prędkość dowolnego punktu M bryły można wyrazić wzorem:

V=V_C+ ω×CM

Ponieważ z założenia prędkość punktu C jest równa zeru więc prędkość punktu M będzie opisana wzorem:

V= ω×CM

Z otrzymanego wzoru wynika , że prędkość dowolnego punktu M bryły jest prostopadła do prostej łączącej punkt M z chwilowym środkiem obrotu C. ponadto wektory ω i CM są prostopadłe więc moduł prędkości:

V= ωCM

8. Omówić metody wyznaczania przyspieszeń punktów ciała sztywnego w ruchu płaskim.

Przyspieszenie dowolnego punktu figury płaskiej poruszającej się w swojej płaszczyźnie równe jest sumie geometrycznej przyspieszenia dowolnie obranego bieguna A oraz przyspieszenia punktu B względem bieguna A (tj. przyspieszenia punktu B w ruchu obrotowym figury wokół bieguna).

Aby otrzymać przyspieszenie dowolnego punktu figury płaskiej leżącego na prostej AB, należy do przyspieszenia bieguna A dodać geometrycznie wektor przedstawiający przyspieszenie tego punktu względem bieguna. Ponieważ to ostatnie przyspieszenie jest proporcjonalne do odległości punktu od bieguna oraz nachylone jest do prostej AB pod kątem, który nie zależy od wspomnianej odległości, to dla otrzymania przyspieszenia dowolnego punktu tej prostej (np. pkt D), należy wykonać konstrukcję geometryczną pokazaną na zamieszczonym i zajebiście wykonanym obrazku powyżej

Dynamika nieswobodnego punktu materialnego

Ruch takiego punktu możemy rozpatrywać jako ruch punktu swobodnego pod wpływem sił czynnych P i biernych R. Równanie wektorowe nieswobodnego punktu materialnego o stałej masie m ma postać:

(7)

W układzie naturalnym równanie (7) przyjmuje postacie:

,

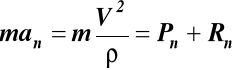
9. Omówić równania różniczkowe ruchu dla nieswobodnego punktu materialnego.

Równania różniczkowe ruchu dla nieswobodnego punktu materialnego:

*Ogólne:

*Gdy linia

ruchu jest

idealnie gładka:

*Gdy torem

jest łuk koła o

promieniu r:

10. Omówić zasadę d'Alemberta.

ZASADA d'ALEMBERTA:

W czasie ruchu dowolnego układu punktów materialnych siły rzeczywiste działające na punkty tego układu równoważą się w każdej chwili z odpowiednimi siłami bezwładności.

Zgodnie z wygłoszoną wyżej zasadą siły rzeczywiste działające na punkty materialne rozpatrywanego układu oraz pomyślane siły, które nazwaliśmy siłami bezwładności, muszą spełniać ustalone w statyce ogólne równania równowagi. Tak więc suma geometryczna wszystkich sił rzeczywistych i wszystkich sił bezwładności musi być równa zeru oraz suma geometryczna ich momentów względem dowolnie obranego bieguna 0 musi także znikać. Wynikją stąd:

WEKTOROWE RÓWNANIA RÓWNOWAGI:

SKALARNE RÓWNANIA RÓWNOWAGI:

,
,
,

,

,

,

gdzie: xi,yi,zi oznaczają tu współrzędne punktu o masie mi.

11. Podać sposób rozwiązania równania różniczkowego drgań wymuszonych nietłumionych.

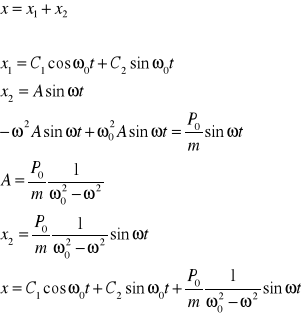
Warunki początkowe

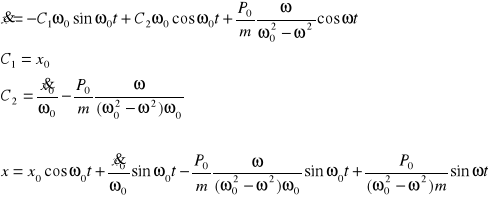
Podać właściwości pochodnej wektora jednostkowego (wersora).

Gdy funkcja wektorowa jest zapisana analitycznie w prostokątnym nieruchomym układzie współrzędnych x, y, z, wtedy jej pochodną po wykorzystaniu wzorów na różniczkowanie sumy i iloczynu funkcji wyraża wzór:

Ponieważ wersory osi nieruchomego układu współrzędnych są wektorami stałymi, mamy:

a stąd ostatecznie:

Z powyższego wynika, że współrzędne pochodnej wektora są równe pochodnym odpowiednich współrzędnych tego wektora. Pochodne wyższych rzędów funkcji wektorowych obliczamy analogicznie do

funkcji skalarnych.

P_B/A

P_D/A

P_A

P_B

P_A

P_D

P_A

B

D

A

_v

R

β

l

P

τ

---