Zadanie II-01

Wyraź wybrane jednostki pochodne za pomocą jednostek podstawowych: N, W, F, T.

Rozwiązanie:

Początek formularza

Niuton ( N)

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Wat ( W)

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Farad ( F)

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Tesla ( T)

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Dół formularza

Zadanie II-02

Wyraź wybrane jednostki pochodne za pomocą jednostek podstawowych: J, C, , Pa.

Rozwiązanie:

Początek formularza

Dżul ( J)

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Kulomb ( C)

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Om ( )

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Paskal ( Pa)

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Dół formularza

Zadanie III-01

Samochód jedzie z miejscowości A do miejscowości B oddalonych o d₁ = 10 km, a następnie wraca do miejscowości C oddalonej od A o d₂ = 4 km. Oblicz drogę przebytą przez samochód oraz jego przemieszczenie. Załóż, ze wszystkie miejscowości leżą na jednej prostej. Zakładając, ze całkowity czas ruchu samochodu wynosi t = 20 min, oblicz średnią prędkość oraz szybkość ruchu tego samochodu.

Rozwiązanie:

Początek formularza

Całkowita droga wynosi: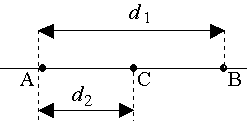

1. -
-20 km

--

2. -
-14 km

--

3. -
-16 km

--

4. -
-4 km

--

Długość wektora przemieszczenia wynosi:

1. -
-20 km

--

2. -
-14 km

--

3. -
-16 km

--

4. -
-4 km

--

Średnia szybkość ruchu wynosi:

1. -
-60 km/h

--

2. -
-42 km/h

--

3. -
-48 km/h

--

4. -
-12 km/h

--

Długość wektora średniej prędkości wynosi:

1. -
-60 km/h

--

2. -
-42 km/h

--

3. -
-48 km/h

--

4. -
-12 km/h

--

Dół formularza

Zadanie III-02

Z jaką średnią szybkością poruszał się motocyklista, który przebył drogę z miasta A do miasta B w ciągu 4 godzin, oraz drogę powrotną w ciągu 5 godzin ? Odległość między miastami wynosi 200 km.

Rozwiązanie:

Początek formularza

Całkowita droga wynosi:

1. -
-0 km

--

2. -
-400 km

--

3. -
-200 km

--

4. -
-100 km

--

Całkowity czas ruchu wynosi:

1. -
-9 h

--

2. -
-10 h

--

3. -
-8 h

--

4. -
-1 h

--

Średnia szybkość ruchu wynosi:

1. -
-50 km/h

--

2. -
-40 km/h

--

3. -
-45 km/h

--

4. -
-44,4 km/h

--

co daje:

1. -
-12,3 m/s

--

2. -
-11,1 m/s

--

3. -
-12,5 m/s

--

4. -
-13 m/s

--

Dół formularza

Zadanie III-03

Łódź płynie z miejscowości A do B, tam i z powrotem, przez 3 godziny. Prędkość łodzi względem wody wynosi 6 m/s; stała prędkość nurtu rzeki wynosi 4 m/s. Oblicz średnią szybkość łodzi względem brzegów. Ile wynosi odległość od A do B ?

Rozwiązanie:

Początek formularza

Prędkość łodzi z prądem rzeki wynosi:

1. -
-6 m/s

--

2. -
-21,6 km/h

--

3. -
-10 m/s

--

4. -
-4 m/s

--

Prędkość łodzi pod prąd rzeki wynosi:

1. -
-2 m/s

--

2. -
-4 m/s

--

3. -
-14,4 m/s

--

4. -
-10 m/s

--

Odległość między miejscowościami A i B:

1. -
-10 km

--

2. -
-5 km

--

3. -
-18 km

--

4. -
-20 km

--

Średnia szybkość łodzi względem brzegów:

1. -
-6 m/s

--

2. -
-12 km/h

--

3. -
-5 km/h

--

4. -
-4 m/s

--

Dół formularza

Zadanie III-04

W tym samym momencie z lotniska w Krakowie wyleciały do Poznania helikopter i samolot. Helikopter leciał prosto do celu, natomiast samolot miał międzylądowanie w Warszawie. Ile czasu trwało to międzylądowanie, jeżeli obydwa pojazdy doleciały do Poznania w tym samym momencie? Przyjąć prędkość helikoptera V_H = 250 km/h, a prędkość samolotu V_S = 620 km/h. Droga przez Warszawę wynosi d_W = 620 km, a trasa bezpośrednia ma długość d = 375 km.

Rozwiązanie:

Początek formularza

Czas lotu helikoptera:

1. -
-80 min

--

2. -
-1,5 h

--

3. -
-4000 s

--

4. -
-95 min

--

Czas lotu samolotu:

1. -
-60 min

--

2. -
-1,5 h

--

3. -
-4000 s

--

4. -
-30 min

--

Czas międzylądowania:

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Co daje:

1. -
-20 min

--

2. -
-15 min

--

3. -
-30 min

--

4. -
-45 min

--

Dół formularza

Zadanie III-05

Turysta udaje się z miejscowości A do odległej o 30 km miejscowości B. Ma do wyboru dwa sposoby przebycia tej drogi. W pierwszym z nich przez połowę drogi jedzie rowerem, a następnie maszeruje piechotą. Drugi sposób polega na jeździe rowerem przez połowę czasu, a następnie marsz. Którym sposobem turysta szybciej dojdzie do celu? Jakie są średnie szybkości w obydwu przypadkach? Prędkości marszu i jazdy na rowerze wynoszą odpowiednio: V_M = 6 km/h i V_R = 24 km/h.

Rozwiązanie:

Początek formularza

Pierwszy sposób (równe drogi) Czas ruchu:

1. -
-3 h

--

2. -
-187,5 min

--

3. -
-135,5 min

--

4. -
-2,5 h

--

Średnia prędkość:

1. -
-9,6 km/h

--

2. -
-5,5 m/s

--

3. -
-15 km/h

--

4. -
-4 m/s

--

Drugi sposób (równe czasy): Czas ruchu:

1. -
-2 h

--

2. -
-90 min

--

3. -
-140 min

--

4. -
-2,5 h

--

Średnia prędkości:

1. -
-4 m/s

--

2. -
-20 km/h

--

3. -
-15 km/h

--

4. -
-5 m/s

--

Dół formularza

Zadanie III-06

Samochód jadący z prędkością V₀ = 54 km/h zatrzymuje się po czasie t = 3 sekundy od chwili rozpoczęcia hamowania. Ile wynosi droga hamowania? Z jakim opóźnieniem poruszał się samochód?

Rozwiązanie:

Początek formularza

Prędkość końcowa samochodu wynosi:

1. -
-54 km/h

--

2. -
-0 km/h

--

3. -
-18 km/h

--

4. -
-27 km/h

--

Przyspieszenie ruchu samochodu:

1. -
--5 m/s²

--

2. -
-0 m/s²

--

3. -
-18 m/s²

--

4. -
--10 m/s²

--

Droga przebyta przez samochód wyraża się wzorem:

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

i wynosi:

1. -
-12 m

--

2. -
-22,5 m

--

3. -
-15 m

--

4. -
-17,5 m

--

Dół formularza

Zadanie III-07

Ania rzuca piłką do góry i przed złapaniem jej trzy razy klaszcze w dłonie. Z jaką minimalną prędkością V₀ musi wyrzucić piłkę, aby zdążyć ją złapać? Na jaką wysokość h dotrze piłka? Czas jednego klaśnięcia wynosi t_K = 0,5 s. Oznaczenie: t - całkowity czas ruchu

Rozwiązanie:

Początek formularza

Czas wznoszenia się piłki wynosi:

1. -
-0,5 s

--

2. -
-1,5 s

--

3. -
-0,75 s

--

4. -
-1 s

--

Prędkość początkowa ruchu V₀ =

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Wysokość, na jaką dotrze piłka wyraża się wzorem h =

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

i wynosi:

1. -
-2,8 m

--

2. -
-2,2 m

--

3. -
-3,2 m

--

4. -
-1,8 m

--

Dół formularza

Zadanie III-08

Wyrzucona przez chłopca piłka dociera na wysokość h₁ = 8 metrów. Po jakim czasie t musi on rzucić drugą piłkę, aby zderzyły się one na wysokości h₂ = 1 m? Obydwie piłki wyrzucane są z tą samą prędkością początkową V₀ , skierowaną pionowo do góry.

Rozwiązanie:

Początek formularza

Prędkość wyrzutu piłki V₀ =

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Równanie ruchu piłki:

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Powyższe równanie jest równaniem kwadratowym ze względu na czas i jego wyróżnik dla y = h₂ wynosi:

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Odstęp czasowy między rzutami t =

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Dół formularza

Zadanie III-09

Jaką maksymalną wysokość h_max osiąga ciało, które rzucone pionowo do góry, po czasie t = 2 s znajduje się na wysokości h = 2 m? W jakiej fazie ruchu (wznoszenie, opadanie) znajduje się ciało po owych dwóch sekundach?

Rozwiązanie:

Początek formularza

Prędkość początkowa ciała V₀ =

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Czas wznoszenia t_W =

1. -
-1,1 s

--

2. -
-0,8 s

--

3. -
-2,1 s

--

4. -
-2 s

--

Maksymalna wysokość wyraża się wzorem:

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

i wynosi:

1. -
-3 m

--

2. -
-6 m

--

3. -
-4 m

--

4. -
-5 m

--

Dół formularza

Zadanie III-10

Po jakim czasie i pod jakim kątem ciało uderzy w podłoże, jeżeli rzucimy je z poziomą prędkością początkową V₀ = 5 m/s, z wysokości h = 3 m?

Rozwiązanie:

Początek formularza

Czas spadania ciała: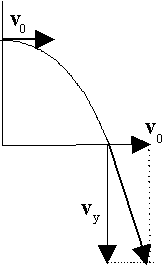

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Prędkość pionowa podczas upadku V_Y=

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Tangens kąta upadku:

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Kąt upadku wynosi:

1. -
-48^o

--

2. -
-30^o

--

3. -
-56,9^o

--

4. -
-62,1^o

--

Dół formularza

Zadanie III-11

Jaką prędkość V₀ należy nadać piłce golfowej, aby upadła w odległości d = 20 m od miejsca wybicia i osiągnęła maksymalną wysokość h = 5 m? Oblicz kąt początkowy tego rzutu.

Rozwiązanie:

Początek formularza

Korzystając ze wzorów na zasięg rzutu d =

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

i maksymalną wysokość h_max =

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

otrzymujemy tangens kąta wybicia:

1. -
-1

--

2. -
-

--

3. -
-

--

4. -
-

--

oraz prędkość początkową V₀ =

1. -
-8 m/s

--

2. -
-14 m/s

--

3. -
-20 m/s

--

4. -
-18 m/s

--

Dół formularza

Zadanie III-12

Koło zamachowe o promieniu R = 20 cm rozpędza się ruchem jednostajnie przyspieszonym, z przyspieszeniem kątowym  = 0,25 s^-2. Po jakim czasie t, dla punktów na obwodzie koła, wartość przyspieszenia liniowego będzie równa przyspieszeniu dośrodkowemu? O jaki kąt  koło zdąży się obrócić do tego czasu? Ile wynoszą powyższe przyspieszenia w tym momencie? Oblicz przyspieszenie wypadkowe a.

Rozwiązanie:

Początek formularza

Równość przyspieszenia liniowego i dośrodkowego wyraża wzór:

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Czas, po którym nastąpi wyrównanie się przyspieszeń wynosi t =

1. -
-1 s

--

2. -
-2 s

--

3. -
-2,5 s

--

4. -
-4,2 s

--

Do tego czasu koło zdąży obrócić się o kąt  =

1. -
-0,5 rad

--

2. -
-1,5  rad

--

3. -
-112^o

--

4. -
-235^o

--

W tym punkcie przyspieszenie wypadkowe wynosi a =

1. -
-2 m/s²

--

2. -
-0,07 m/s²

--

3. -
-4,2 m/s²

--

4. -
-9,81 m/s²

--

Dół formularza

Zadanie III-13

Ile czasu upływa pomiędzy dwoma kolejnymi momentami spotkań wskazówki minutowej z godzinową?

Rozwiązanie:

Początek formularza

Prędkość kątowa wyraża się wzorem  =

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Różnica kątów zakreślanych między spotkaniami wskazówek wynosi:

1. -
-
rad

--

2. -
-
rad

--

3. -
-
rad

--

4. -
-
rad

--

Czas miedzy spotkaniami wyraża wzór ( T₁ = 1 h, T₂ = 12 h ):

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

i wynosi około:

1. -
-3300 s

--

2. -
-73 min

--

3. -
-3927 s

--

4. -
-1,2 h

--

Dół formularza

Zadanie III-14

Z jaką prędkością V opada spadochroniarz, jeżeli siła oporu F_o jaka działa w tym ruchu jest proporcjonalna do prędkości, ze współczynnikiem równym  = 200 kg/s. Całkowita masa skoczka wynosi m = 80kg.

Rozwiązanie:

Początek formularza

Ciężar spadochroniarza wynosi około:

1. -
-80 N

--

2. -
-160 N

--

3. -
-785 N

--

4. -
-850 N

--

Siła oporu powietrza wyraża się wzorem F_O =

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Równowagowa prędkość opadania wynosi V =

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Co daje:

1. -
-3,9 m/s

--

2. -
-2,1 m/s

--

3. -
-4,5 m/s

--

4. -
-5 m/s

--

Dół formularza

Zadanie III-15

Jakie masy m₁ i m₂ należy zawiesić na linach, aby układ przedstawiony na rysunku pozostawał w spoczynku? Przyjąć: m₃ = 10 kg,  = 45^o,  = 30^o.

Rozwiązanie:

Początek formularza

Równowaga sił w kierunku poziomym: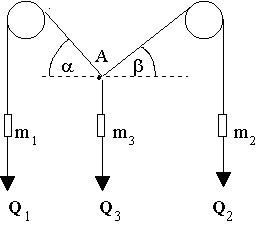

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Równowaga sił w kierunku pionowym:

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Masa m₁ wynosi około:

1. -
-5 kg

--

2. -
-9,0 kg

--

3. -
-7,3 kg

--

4. -
-10 kg

--

Masa m₂ wynosi około:

1. -
-5 kg

--

2. -
-9,0 kg

--

3. -
-7,3 kg

--

4. -
-10 kg

--

Dół formularza

Zadanie III-16

Chłopiec ciągnie sanki za sznur, który tworzy kąt  = 30^o z podłożem. Jaką siłą musi działać chłopiec na sanki, aby wciągnąć je na zbocze o kącie nachylenia  = 15^o?
Masa sanek wynosi m = 10 kg. Tarcie zaniedbać.

Rozwiązanie:

Początek formularza

Składowa siły ciężkości ściągająca sanki w dół zbocza Q₁ =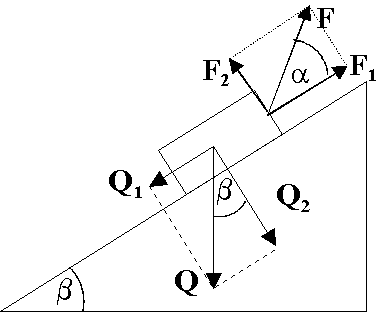

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Składowa siły naciągu sznurka wzdłuż zbocza F₁ =

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Z równowagi sił F =

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

I wynosi około:

1. -
-29,3 N

--

2. -
-62,3 N

--

3. -
-48,2 N

--

4. -
-21,4 N

--

Dół formularza

Zadanie III-17

Jaką siłą F należy działać na masę m = 1 kg, aby w ciągu t = 1 s podnieść ją na wysokość h = 2m?

Rozwiązanie:

Początek formularza

Równanie ruchu ciała:

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Przyspieszenie ruchu wyraża się wzorem a =

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Siła F =

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Co daje:

1. -
-13,8 N

--

2. -
-9,8 N

--

3. -
-11,2 N

--

4. -
-4,9 N

--

Dół formularza

Zadanie III-18

Ile czasu zajmuje zsuwanie się ciała z wysokości h = 1 m umieszczonego na równi pochyłej o kącie nachylenia  = 30^o ? Porównaj ten wynik z czasem swobodnego spadku z identycznej wysokości. Ciało zsuwa się bez tarcia.

Rozwiązanie:

Początek formularza

Równanie ruchu ciała przyjmuje postać: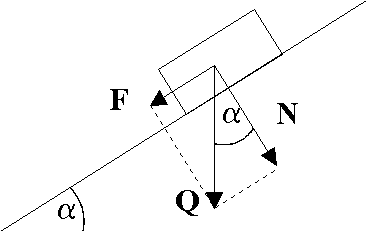

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Czas ruchu obliczamy z drogi i wynosi on t =

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Czas swobodnego spadku wyraża się wzorem t_S =

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Stosunek czasu ruchu do czasu swobodnego spadku wynosi t/t_S=

1. -
-1

--

2. -
-1,3

--

3. -
-2

--

4. -
-2,8

--

Dół formularza

Zadanie III-19

Porównaj siły hamowania samochodu, jeżeli zatrzymuje się on w czasie t = 3 s na suchej nawierzchni, a z kolei na oblodzonej jezdni droga hamowania wynosi s = 60 m. Prędkość początkowa samochodu w obu przypadkach wynosi V₀ = 60 km/h.

Rozwiązanie:

Początek formularza

Opóźnienie samochodu na suchej nawierzchni obliczamy ze wzoru:

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Opóźnienie samochodu na oblodzonej nawierzchni:

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Stosunek siły hamowania na suchej nawierzchni do siły hamowania na nawierzchni oblodzonej wyraża się wzorem F₁/F₂=

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Co daje:

1. -
-2

--

2. -
-1,5

--

3. -
-2,4

--

4. -
-3,2

--

Dół formularza

Zadanie III-20

Ile wynosi siła wzajemnego oddziaływania między dwoma wagonami tramwaju o masach odpowiednio równych m₁ = 10 ton i m₂ = 8 ton, jeśli na pierwszy wagon działa siła F = 10 kN ? Oblicz, z jakim największym przyspieszeniem może poruszać się tramwaj, jeżeli wytrzymałość połączenia między wagonami wynosi N_max = 40 kN.

Rozwiązanie:

Początek formularza

Równanie ruchu pierwszego wagonu: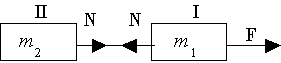

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Równanie ruchu drugiego wagonu:

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Siła naciągu N =

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Maksymalne przyspieszenie tramwaju a_max =

1. -
-5 m/s²

--

2. -
-2 m/s²

--

3. -
-10 m/s²

--

4. -
-8 m/s²

--

Dół formularza

Zadanie III-21

Dwa ciała o masach m₁ = 1 kg i m₂ = 2 kg zwisają na linie z dwóch stron nieważkiego bloczka, który obraca się bez tarcia. Ile wynosi naciąg liny N? Jaka siła P przenosi się na zawieszenie osi bloczka?

Rozwiązanie:

Początek formularza

Równanie ruchu pierwszego ciała: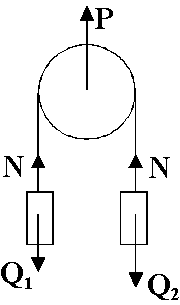

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Równanie ruchu drugiego ciała:

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Siła naciągu N =

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Siła przenoszona przez bloczek P =

1. -
-19,3 N

--

2. -
-26,2 N

--

3. -
-29,4 N

--

4. -
-22,6 N

--

Zadanie III-22

Jak zmienia się przyspieszenie grawitacyjne, jeżeli przesuwamy się od środka Ziemi ku jej powierzchni? M_Z , R_Z - masa i promień Ziemi.

Rozwiązanie:

Początek formularza

Zależność przyspieszenia grawitacyjnego od odległości, dla sferycznego rozkładu masy M(r), wyraża wzór g( r) =

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Masa M( r) zmienia się z odległością od środka Ziemi zgodnie ze wzorem M( r) =

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Przyspieszenie grawitacyjne zmienia się według wzoru g( r) =

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Co schematycznie ilustruje wykres g( r)

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Dół formularza

Dół formularza

Zadanie III-23

Wiedząc, że masa Księżyca jest 81 razy mniejsza od masy Ziemi, a przyspieszenie grawitacyjne na Księżycu jest 6 razy mniejsze niż na Ziemi, oblicz ile razy promień Księżyca jest mniejszy od promienia Ziemi. ( M_Z = 81 M_K , g_Z = 6 g_K)

Rozwiązanie:

Początek formularza

Przyspieszenie grawitacyjne na powierzchni Ziemi wynosi g_Z =

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Zatem g_z/g_k =

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Stąd R_z/R_k =

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Co daje:

1. -
-6,1

--

2. -
-21,2

--

3. -
-3,7

--

4. -
-18,5

--

Dół formularza

Zadanie III-24

Zakładając, że masa Księżyca jest 81 razy mniejsza niż masa Ziemi, oblicz, w jakiej odległości od środka Ziemi, w stosunku do odległości R_ZK środków Księżyca i Ziemi, znajduje się punkt "równowagi grawitacyjnej" na linii Ziemia-Księżyc.

Rozwiązanie:

Początek formularza

Siłę grawitacyjnego przyciągania Ziemi w punkcie odległym o R₁ od jej środka, wyraża wzór:

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

W tym samym punkcie, siła grawitacyjnego przyciągania Księżyca dana jest wyrażeniem:

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Równowagę sił wyraża równość:

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Której rozwiązaniem jest R₁/R_ZK=

1. -
-0,95

--

2. -
-0,90

--

3. -
-0,78

--

4. -
-0,65

--

Dół formularza

Zadanie III-25

Ciało spoczywa na równi pochyłej o zmiennym kącie nachylenia . Oblicz kąt graniczny, tj. taki, powyżej którego ciało zaczyna się zsuwać. Współczynnik tarcia wynosi f = 0,577, a Q jest ciężarem ciała.

Rozwiązanie:

Początek formularza

Siła tarcia statycznego T spełnia zależność: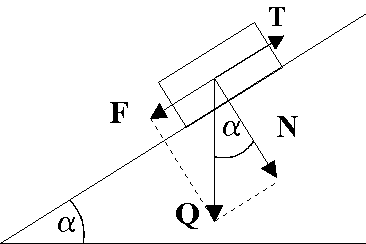

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Równowaga sił dla kąta granicznego wyraża się wzorem:

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Stąd:

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Oraz kąt graniczny _gr =

1. -
-15^o

--

2. -
-30^o

--

3. -
-60^o

--

4. -
-45^o

--

Dół formularza

Zadanie III-26

Chłopiec ciągnie pod górę sanki za sznurek skierowany pod kątem  = 20^o do stoku góry, który z kolei jest nachylony pod kątem =30^o do poziomu. Ile wynosi siła z jaką chłopiec ciągnie sanki, jeżeli współczynnik tarcia wynosi f = 0,2, a masa sanek jest równa m = 10 kg? Przyjmij, że chłopiec porusza się ruchem jednostajnym.

Rozwiązanie:

Początek formularza

Równanie ruchu przyjmuje postać: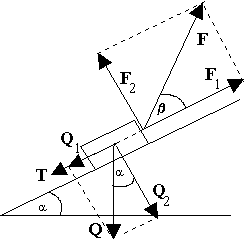

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-

--

Siła tarcia T =

1. -
-

--

2. -
-

--

3. -
-

--

4. -
-0

--

Siła F =

1.

2.

3.

4.

Co daje:

1.
58,2 N

2.
65,5 N

3.
82,1 N

4.
98,1 N

Dół formularza

Zadanie III-27

Z jakim przyspieszeniem porusza się ciało zsuwające się z równi pochyłej o kącie nachylenia  = 45^o, jeżeli współczynnik tarcia wynosi f = 0,4?

Rozwiązanie:

Początek formularza

Równanie ruchu ciała: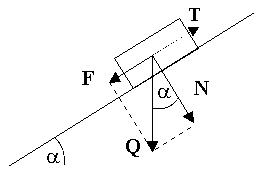

1.

2.

3.

4.

Siła tarcia T =

1.

2.

3.

4.

Przyspieszenie ciała a =

1.

2.

3.

4.

Co daje:

1.
9,81 m/s²

2.
4,16 m/s²

3.
2,43 m/s²

4.
3,51 m/s²

Dół formularza

Zadanie III-28

Ile razy zwiększy się czas spadania ciała w windzie, jeżeli ruszyła ona w dół z przyspieszeniem a_u = 0,5 g?

Rozwiązanie:

Początek formularza

Czas spadku ciała w windzie nieruchomej t₀ =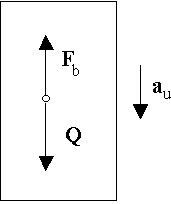

1.

2.

3.

4.

Równanie ruchu ciała w windzie:

1.

2.

3.

4.
a=0

Czas spadku w windzie poruszającej się t =

1.

2.

3.

4.

Stosunek t/t₀ =

1.
2

2.

3.

4.

Dół formularza

Zadanie III-29

Samochód o masie m = 1 tony jedzie z prędkością v = 60 km/h po moście w kształcie wypukłego łuku. Ile wynosi siła nacisku samochodu na jezdnię w środkowej części mostu, jeżeli promień krzywizny w tym miejscu wynosi R = 100 m?
Q - ciężar samochodu
F_od - siła odśrodkowa

Rozwiązanie:

Początek formularza

Siła nacisku samochodu na most N =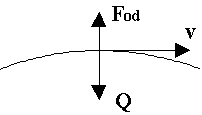

1.

2.

3.

4.

Siła odśrodkowa F_od =

1.

2.

3.

4.

Ostatecznie, siła nacisku N =

1.

2.

3.

4.

Co daje:

1.
9810 N

2.
7 kN

3.
8520 N

4.
3510 N

Dół formularza

Zadanie III-30

Z jaką maksymalną prędkością może samochód pokonać zakręt o promieniu krzywizny R = 20 m, jeżeli współczynnik tarcia wynosi f = 0,5 ?

Rozwiązanie:

Początek formularza

Aby samochód nie wypadł z trasy musi być spełniony warunek :

1.

2.

3.

4.

Siła odśrodkowa F_odśrod =

1.

2.

3.

4.

Maksymalna prędkość:

1.

2.

3.

4.

Co daje:

1.
9,9 m/s

2.
6,2 m/s

3.
18 km/h

4.
54 km/h

Dół formularza

Zadanie III-31

Z jakim przyspieszeniem toczy się (bez poślizgu) walec po równi pochyłej o kącie nachylenia  = 30^o ?
I - moment bezwładności walca względem osi 0

Rozwiązanie:

Początek formularza

Równanie ruchu postępowego: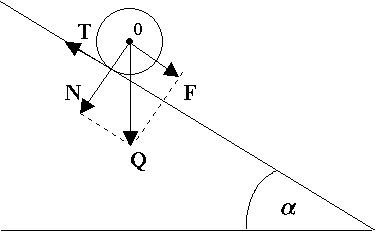

1.

2.

3.

4.

Równanie ruchu obrotowego:

1.

2.

3.

4.

Przyspieszenie liniowe:

1.

2.

3.

4.

Co daje:

1.
3,27 m/s²

2.
1,18 m/s²

3.
2,52 m/s²

4.
5,08 m/s²

Dół formularza

Zadanie III-32

Ile wynosi siła tarcia podczas toczenia się ( bez poślizgu) walca o masie m = 1 kg po równi pochyłej o kącie nachylenia  = 30^o ?
Moment bezwładności walca:I = 0,5mR²,
współczynnik tarcia - f

Rozwiązanie:

Początek formularza

Równanie ruchu postępowego: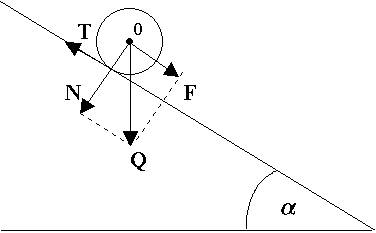

1.

2.

3.

4.

Równanie ruchu obrotowego:

1.

2.

3.

4.

Siła tarcia:

1.

2.

3.

4.

Co daje:

1.
1,6N

2.
0,8N

3.
brak danych

4.
2,1N

Zadanie III-33

Dla jakiego maksymalnego kąta walec będzie się toczył po równi pochyłej bez poślizgu ? Współczynnik tarcia wynosi:
, a moment bezwładności walca:
.

Rozwiązanie:

Początek formularza

Równanie ruchu postępowego: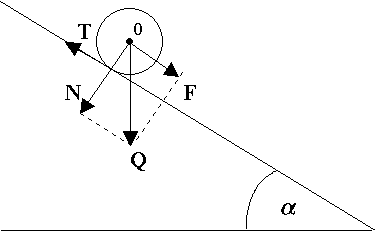

1.

2.

3.

4.

Równanie ruchu obrotowego:

1.

2.

3.

4.

Siła tarcia statycznego musi spełniać warunek:

1.

2.

3.

4.

Kąt graniczny, powyżej którego występuje poślizg:

1.
45^o

2.
30^o

3.
60^o

4.
55^o

Dół formularza

vZadanie III-34

Z jakim przyspieszeniem liniowym toczy się z poślizgiem walec po równi pochyłej o kącie nachylenia =60^o? Współczynnik tarcia wynosi f=0,1.

Rozwiązanie:

Początek formularza

Równanie ruchu postępowego: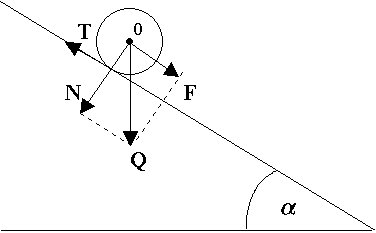

1.

2.

3.

4.

Tarcie kinetyczne T=

1.

2.

3.

4.

Przyspieszenie a =

1.

2.

3.

4.

Co daje:

1.
8,5 m/s²

2.
9,8 m/s²

3.
4,9 m/s²

4.
8 m/s²

Dół formularza

vZadanie III-35

Z jakim przyspieszeniem kątowym toczy się z poślizgiem walec po równi pochyłej o kącie nachylenia  = 60^o?
Współczynnik tarcia wynosi f = 0,1 , a promień walca R = 5 cm. Moment bezwładności walca:

Rozwiązanie:

Początek formularza

Równanie ruchu obrotowego: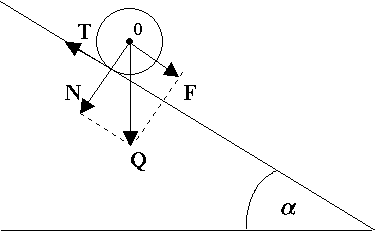

1.

2.

3.

4.

Tarcie kinetyczne T =

1.

2.

3.

4.

Przyspieszenie kątowe =

1.

2.

3.

4.

Co daje:

1.
9,81 1/s²

2.
12,4 1/s²

3.
19,6 1/s²

4.
25,1 1/s²

Dół formularza

Zadanie III-35

Z jakim przyspieszeniem kątowym toczy się z poślizgiem walec po równi pochyłej o kącie nachylenia  = 60^o?
Współczynnik tarcia wynosi f = 0,1 , a promień walca R = 5 cm. Moment bezwładności walca:

Rozwiązanie:

Początek formularza

Równanie ruchu obrotowego: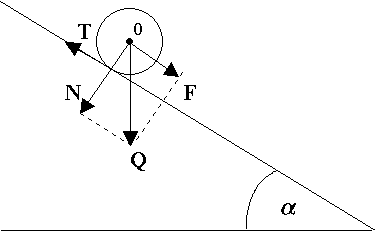

1.

2.

3.

4.

Tarcie kinetyczne T =

1.

2.

3.

4.

Przyspieszenie kątowe =

1.

2.

3.

4.

Co daje:

1.
9,81 1/s²

2.
12,4 1/s²

3.
19,6 1/s²

4.
25,1 1/s²

Dół formularza

Zadanie III-36

Przez bloczek o promieniu R = 10 cm i momencie bezwładności I = 0,01 kg m² przerzucono sznurek, na końcach którego zawieszono masy m₁ = 1 kg i m₂ = 2 kg. Ile wynosi przyspieszenie układu, jeżeli sznurek nie ślizga się po bloczku? Ile wynoszą siły naciągu sznurka po obu stronach bloczka?

Rozwiązanie:

Początek formularza

Równanie ruchu masy m₁:

1.

2.

3.

4.

Równanie ruchu masy m₂:

1.

2.

3.

4.

Równanie ruchu bloczka:

1.

2.

3.

4.

Przyspieszenie a =

1.

2.

3.

4.

Dół formularza

Zadanie III-37

Przez bloczek o promieniu R = 10 cm i momencie bezwładności I = 0,01 kg m² przerzucono sznurek, na końcach którego zawieszono masy m₁ = 1 kg i m₂ = 2 kg. Ile wynosi przyspieszenie układu, jeżeli sznurek nie ślizga się po bloczku? Ile wynosi siła naciągu sznurka na ciało o masie m₁ ?

Rozwiązanie:

Początek formularza

Równania ruchu masy m₁: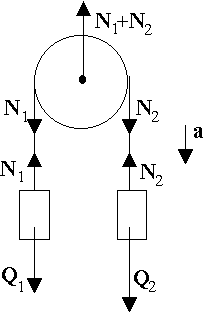

1.

2.

3.

4.

Równania ruchu masy m₂:

1.

2.

3.

4.

Równanie ruchu bloczka:

1.

2.

3.

4.

Siła nacisku N₁ =

1.

2.

3.

4.

Dół formularza

Zadanie III-38

Jednorodna belka o masie M = 100 kg i długości l = 4 m wisi poziomo na linach zaczepionych do jej końców. Ile wynoszą naciągi lin, jeżeli w odległości a = 1 m od końca belki doczepiono masę m = 40 kg ?

Rozwiązanie:

Początek formularza

Równowaga sił:

1.

2.

3.

4.

Równowaga momentów sił względem punktu O:

1.

2.

3.

4.

Siła napięcia N₁ =

1.

2.

3.

4.

Siła napięcia N₂ =

1.

2.

3.

4.

Dół formularza

Zadanie III-39

Drabina o masie m = 20 kg stoi oparta o gładką ścianę. Ile wynosi współczynnik tarcia drabiny o podłoże, jeżeli zaczyna się ona zsuwać przy kącie  = 45^o?

Rozwiązanie:

Początek formularza

Równowaga sił: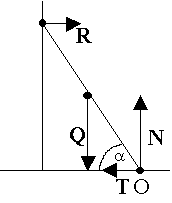

1.

2.

3.

4.

Równowaga momentów sił względem punktu O:

1.

2.

3.

4.

Współczynnik tarcia
=

1.

2.

3.

4.

Co daje:

1.
0,5

2.
1

3.
2

4.
0,3

Dół formularza

Zadanie III-40

Drabina o masie m = 20 kg stoi oparta o gładką ścianę pod kątem  = 45^o. Ile wynosi siła z jaką drabina działa na ścianę?

Rozwiązanie:

Początek formularza

Równowaga sił: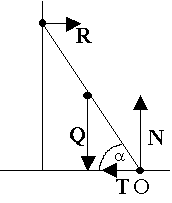

1.

2.

3.

4.

Równowaga momentów sił:

1.

2.

3.

4.

Siła reakcji ściany R =

1.

2.

3.

4.

Co daje:

1.
49 N

2.
55 N

3.
123 N

4.
98 N

Dół formularza

Zadanie III-41

Ciało o masie m = 50 kg podnosimy przy użyciu bloczka ruchomego. Jaką siłą należy ciągnąć za linę przerzuconą przez bloczek?

Rozwiązanie:

Początek formularza

Równowaga sił: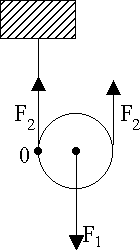

1.

2.

3.

4.

Równowaga momentów sił względem punktu O:

1.

2.

3.

4.

Siła napięcia liny F₂ =

1.

2.

3.

4.

Co daje:

1.
0,245 kN

2.
490 N

3.
327 N

4.
0,5 kN

Dół formularza

Zadanie III-42

Jaką moc P₀ ma silnik tokarki, jeżeli nóż skrawający działa momentem siły równym U = 70 Nm, a tokarka wykonuje 6 obrotów na sekundę (f = 6 1/s)? Sprawność urządzenia wynosi  = 70%.

Rozwiązanie:

Początek formularza

Moc wydzielana na tokarce :

1.

2.

3.

4.

Moc noża skrawającego tokarki:

1.

2.

3.

4.

Stąd moc P₀ =

1.

2.

3.

4.

Co daje:

1.
4,2 kW

2.
3,8 kW

3.
1500 W

4.
2500 W

Dół formularza

Zadanie III-43

Chłopiec ciągnie sanki siłą skierowaną pod kątem  = 30^o do podłoża, poruszając się ruchem jednostajnym. Jaką pracę musi on wykonać na drodze s = 50 m, jeżeli współczynnik tarcia wynosi f = 0,4 , a masa sanek wynosi m = 10 kg?

Rozwiązanie:

Początek formularza

Siła tarcia T =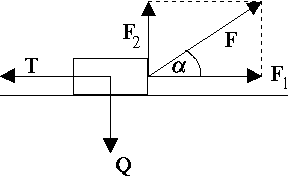

1.

2.

3.

4.

Siła tarcia T jest też równa sile:

1.

2.

3.

4.

Praca siły F jest równa W =

1.

2.

3.

4.

Co daje:

1.
1153 J

2.
1594 J

3.
3570 J

4.
1730 J

Dół formularza

Zadanie III-44

Ile wynosi praca wykonana przez siłę tarcia podczas zsuwania się ciała o masie m = 2 kg umieszczonego na wysokości h = 2 m na równi pochyłej o kącie nachylenia  = 60^o? Współczynnik tarcia wynosi f = 0,2.

Rozwiązanie:

Początek formularza

Siła tarcia: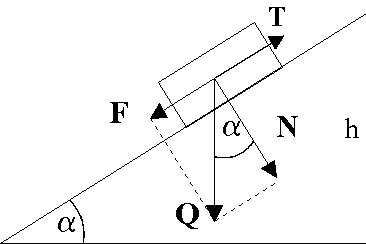

1.

2.

3.

4.

Praca siły tarcia na drodze s to W =

1.

2.

3.

4.

Praca ta jest równa:

1.

2.

3.

4.

Co daje:

1.
8 J

2.
-4,5 J

3.
3,2 J

4.
5,2 J

Dół formularza

Zadanie III-45

Jaką prędkość osiągnie ciało o masie m = 1 kg, które pod działaniem stałej siły F = 20 N jest podnoszone na wysokość h = 2 m? Prędkość początkowa ciała jest równa zeru.

Rozwiązanie:

Początek formularza

Praca wykonana przez siłę jest równa W =

1.

2.

3.

4.
0

Bilans energetyczny:

1.

2.

3.

4.

Prędkość ciała V =

1.

2.

3.

4.

Co daje:

1.
2,2 m/s

2.
0

3.
6,4 m/s

4.
9,8 m/s

Dół formularza

Zadanie III-46

Jaką siłą F należy działać na walec o masie m = 2 kg toczący się bez poślizgu, aby rozpędzić go od prędkości 0 do V = 10 m/s na drodze s = 10 m?

Rozwiązanie:

Początek formularza

Energia kinetyczna wyraża się wzorem:

1.

2.

3.

4.

I jest równa F =

1.

2.

3.

4.

Energia kinetyczna jest równa pracy siły F, stąd obliczamy siłę F =

1.

2.

3.

4.

Co daje:

1.
5 N

2.
10 N

3.
15 N

4.
20 N

Dół formularza

Zadanie III-47

Ciało o masie m = 5 kg zsuwa się z wysokości h = 1 m po równi pochyłej o kącie nachylenia  = 30^o. Ile wynosi energia kinetyczna E_k tego ciała u podstawy równi, jeżeli współczynnik tarcia wynosi f = 0,2 ? Jak wygląda bilans energetyczny układu?

Rozwiązanie:

Początek formularza

Praca siły tarcia W_T =

1.

2.

3.

4.

Energia kinetyczna E_k =

1.

2.

3.

4.

I jest ona równa:

1.

2.

3.

4.

Co daje:

1.
23 J

2.
32 J

3.
48 J

4.
112 J

Dół formularza

Zadanie III-48

Z jakiej minimalnej wysokości h musi stoczyć się kulka (bez poślizgu), aby wykonać "diabelską pętlę" o promieniu R = 20 cm ustawioną na końcu równi? Rozmiary kulki są zaniedbywalnie małe w stosunku do rozmiarów pętli.

Rozwiązanie:

Początek formularza

Porównanie siły odśrodkowej z siłą ciężkości w punkcie B: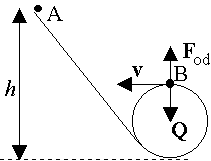

1.

2.

3.

4.

Zasada zachowania energii (punkty A i B):

1.

2.

3.

4.

Stąd wysokość h =

1.
2,7 R

2.
1,5 R

3.
1,8 R

4.
3,4 R

Co daje:

1.
30 cm

2.
3,6 cm

3.
54 cm

4.
68 cm

Dół formularza

Zadanie III-49

Korzystając z zasady zachowania energii wyprowadź wzór na maksymalną wysokość w rzucie ukośnym.

Rozwiązanie:

Początek formularza

Energia w punkcie A to E_A =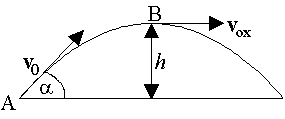

1.

2.

3.

4.

Energia w punkcie B to E_B =

1.

2.

3.

4.

Bilans energetyczny prowadzi do zależności:

1.

2.

3.

4.

Ostatecznie h =

1.

2.

3.

4.

Dół formularza

Zadanie III-50

Piłeczka pingpongowa uderzając w podłoże traci  = 20% swojej energii kinetycznej. Oblicz wysokość na jaką dotrze piłeczka po jednokrotnym, dwukrotnym lub trzykrotnym odbiciu od podłoża, jeżeli została zrzucona z wysokości h = 1 m. Jaki ciąg tworzą te wysokości? Ile wynosi droga s jaką przebędzie piłeczka do momentu zatrzymania się?

Rozwiązanie:

Początek formularza

Wysokość, jaką osiągnie piłeczka po pierwszym odbiciu h₁ =

1.

2.

3.

4.

Wysokość, jaką piłeczka osiągnie po N-tym odbiciu h_N=

1.

2.

3.

4.

Drogę obliczamy z sumy szeregu geometrycznego i wynosi ona s =

1.

2.

3.

4.

Co daje:

1.
5 m

2.
9 m

3.
21 m

4.
32 m

Dół formularza

Zadanie III-51

Pod działaniem siły F = 25 N na drodze s = 2 m ciało pęd ciała osiągnął wartość p = 10
. Jaka jest masa m tego ciała?

Rozwiązanie:

Początek formularza

Energia kinetyczna ciała E_k =

1.

2.

3.

4.

Zamianę pracy siły F na energię kinetyczną wyraża wzór:

1.

2.

3.

4.

Z którego liczymy masę m =

1.

2.

3.

4.

Co daje:

1.
0,5 kg

2.
1 kg

3.
2 kg

4.
2,5 kg

Dół formularza

Zadanie III-52

Ile wynosi średnia siła działająca na ścianę podczas zderzenia z piłką o masie m = 0,5 kg, jeżeli pada ona z prędkością V₁ = 5 m/s, odbija się z prędkością V₂ = 4 m/s, a czas zderzenia wynosi t = 0,25 s ?

Rozwiązanie:

Początek formularza

Druga zasada dynamiki:

1.

2.

3.

4.

Zmiana pędu p =

1.

2.

3.

4.

Ostatecznie siła F =

1.

2.

3.

4.

Co daje:

1.
2 N

2.
12 N

3.
18 N

4.
0,125 N

Dół formularza

Zadanie III-53

Pocisk rzucony jest z prędkością V₀ = 5 m/s pod kątem = 60^odo poziomu, rozrywa się w najwyższym punkcie lotu na dwie równe części tak, że jedna połówka zatrzymuje się, a następnie opada pionowo w dół. Ile wynosi zasięg rzutu d drugiej połówki?

Rozwiązanie:

Początek formularza

Dla kąta  i prędkości początkowej V₀ zasięg rzutu wynosi d =

1.

2.

3.

4.

Po rozerwaniu w najwyższym punkcie pocisku na dwie równe części, jedna z połówek uzyskuje prędkość:

1.

2.

3.

4.

Co pozwoli jej pokonać odległość, liczoną od punktu wystrzelenia pocisku, wynoszącą:

1.

2.

3.

4.

Co daje:

1.
2,5 m

2.
3,3 m

3.
45 m

4.
182 m

Dół formularza

Zadanie III-54

Dwie identyczne kule, z których jedna przed zderzeniem spoczywa, zderzają się sprężyście. Oblicz prędkość kul U₁ i U₂ po zderzeniu, jeżeli prędkość drugiej kuli przed zderzeniem wynosi V₁ .

Rozwiązanie:

Początek formularza

Zasada zachowania pędu:

1.

2.

3.

4.

Zasada zachowania energii:

1.

2.

3.

4.

Prowadzi to do równania kwadratowego:

1.

2.

3.

4.

Którego szukanym rozwiązaniem jest:

1.

2.

3.

4.

Dół formularza

Zadanie III-55

Dwie identyczne kule, z których jedna przed zderzeniem spoczywa, a druga porusza się z prędkością V, zderzają się całkowicie nie sprężyście. Oblicz prędkość U kul po zderzeniu oraz ciepło Q wydzielane w wyniku tego zderzenia.

Rozwiązanie:

Początek formularza

Zasada zachowania pędu:

1.

2.

3.

4.

Zasada zachowania energii mechanicznej:

1.

2.

3.
nie obowiązuje

4.

Prędkość kul po zderzeniu:

1.

2.

3.

4.

Ciepło wydzielone Q =

1.

2.

3.

4.
0

Dół formularza

Zadanie III-56

W klocek o masie M = 1 kg zawieszony na nici uderza centralnie pocisk o masie m = 10 g i prędkości V₀ = 300 m/s i grzęźnie w nim. O jaki kąt odchyli się klocek, jeżeli odległość od punktu zawieszenia do środka masy klocka wynosi l = 1 m?

Rozwiązanie:

Początek formularza

Dla zderzenia w punkcie A korzystamy z zasady zachowania pędu:

1.

2.

3.

4.

Z porównania energii w punktach A i B otrzymujemy wysokość, na jaką klocek odchyli się h =

1.

2.

3.

4.

Kąt nachylenia nici  =

1.

2.

3.

4.

Co daje:

1.
20,5^o

2.
42,1^o

3.
56,6^o

4.
73,2^o

Dół formularza

Zadanie III-57

Ciało o masie m = 100 g zaczepione na sznurku przewleczonym przez pionową rurkę, obraca się po kole o promieniu R₁ = 40 cm, wykonując 1 obrót na sekundę (f₁ = 1 s^-1). Z jaką częstotliwością f₂ będzie poruszać się ciało, jeśli ciągnąc za sznurek zmniejszymy jego promień obrotu do R₂ = 20 cm? Jak zmienia się energia układu?

Rozwiązanie:

Początek formularza

Moment siły F jest równy zeru, więc korzystamy z zasady zachowania momentu pędu:

1.

2.

3.

4.

Moment bezwładności ciała - punktu materialnego I =

1.

2.

3.

4.

Nowa częstotliwość obrotów f₂ =

1.

2.

3.

4.

Co daje:

1.
300 1/min

2.
4 1/s

3.
2 1/s

4.
0,5 1/s

Dół formularza

Zadanie III-58

Odosobniona gwiazda, będąca jednorodną kulą o stałej masie M, kurczy się zmniejszając n-krotnie okres obrotu ₁ wokół własnej osi. Jakiej zmianie w wyniku tego procesu uległo przyspieszenie grawitacyjne na jej biegunach?

Rozwiązanie:

Początek formularza

Przyspieszenie grawitacyjne na biegunie gwiazdy g =

1.

2.

3.

4.

Zasada zachowania momentu pędu:

1.

2.

3.

4.

Stosunek przyspieszeń grawitacyjnych
=

1.

2.

3.

4.

Co daje:

1.

2.

3.

4.

Dół formularza

Zadanie III-59

Cylindryczne naczynie o promieniu R = 20 cm i wysokości h = 50 cm oraz momencie bezwładności I₀ = 1,26 kgm² zostało napełnione wodą ( ρ_w = 1 g/cm³), a następnie wprowadzone w ruch obrotowy wokół osi symetrii z częstością ₁ = 5 rad/s. Po pewnym czasie, w wyniku nieszczelności na osi obrotu, woda wyciekła z cylindra. Ile wynosi nowa częstość obrotu naczynia ₂? Wszelkie opory ruchu zaniedbać. Naczynie jest zamknięte od góry, więc w trakcie wprowadzania w ruch obrotowy powierzchnia wody nie zmienia się.

Rozwiązanie:

Początek formularza

Zasada zachowania momentu pędu:

1.

2.

3.

4.

Moment bezwładności naczynia z wodą I₁ =

1.

2.

3.

4.

Stosunek częstości obrotu naczynia ₂/₁=

1.

2.

3.

4.

Co daje: ₂=

1.
5 rad/s

2.
10 rad/s

3.
20 rad/s

4.
60 rad/s

Dół formularza

Zadanie III-60

Wyprowadź wzór na pierwszą prędkość kosmiczną V₁ przyjmując promień Ziemi R_Z = 6,3810⁶ m oraz przyspieszenie grawitacyjne g = 9,81 m/s².

Rozwiązanie:

Początek formularza

Siła grawitacyjna jest siłą dośrodkową:

1.

2.

3.

4.

Stąd V₁ =

1.

2.

3.

4.

Czyli V₁ =

1.

2.

3.

4.

Co daje:

1.
310⁸m/s

2.
11,2 km/s

3.
7,9 km/h

4.
7,9 km/s

Dół formularza

Zadanie III-61

Wyprowadź wzór na drugą prędkość kosmiczną V₂, wiedząc, że pierwsza prędkość kosmiczna wynosi V₁=7,9 km/s.

Rozwiązanie:

Początek formularza

Zasada zachowania energii dla punktu przy powierzchni Ziemi oraz punktu w nieskończoności:

1.

2.

3.

4.

Stąd V₂ =

1.

2.

3.

4.

Czyli V₂ =

1.
2 V₁

2.
3 V₁

3.

V₁

4.

V₁

Co daje:

1.
310⁸m/s

2.
7,9 km/s

3.
7,9 km/h

4.
11,2 km/s

Dół formularza

Zadanie III-62

Na jaką maksymalną wysokość h ponad Ziemię wzniesie się ciało, które wystrzelono z powierzchni Ziemi z prędkością początkową równą pierwszej prędkości kosmicznej V₁ i skierowaną pionowo do góry?

Rozwiązanie:

Początek formularza

Energia w punkcie A to E_A =

1.

2.

3.

4.

Energia w punkcie B to E_B =

1.

2.

3.

4.
0

Pierwsza prędkość kosmiczna V₁ =

1.

2.

3.

4.

Z porównania energii w punkcie A i B otrzymujemy wysokość h =

1.
30 km

2.

R_Z

3.
3,5 R_Z

4.
R_Z

Dół formularza

Zadanie III-63

Jaką energię Q rozproszył meteor o masie m = 100 g, jeżeli wchodząc w atmosferę ziemską, w odległości h = 100 km od powierzchni Ziemi, miał on prędkość równą pierwszej prędkości kosmicznej V₁ , a uderzył w powierzchnię Ziemi z prędkością V₂ = 100 km/h?

Rozwiązanie:

Początek formularza

Pierwsza prędkość kosmiczna V₁ =

1.
500 m/s

2.
7,9 km/s

3.
11,2 km/s

4.
3x10⁸m/s

Bilans energetyczny:

1.

2.

3.

4.

Energia rozproszona Q =

1.

2.

3.

4.

Co daje:

1.
3,5 MJ

2.
45 kJ

3.
850 J

4.
1,5 GJ

Dół formularza

Zadanie III-64

Wyprowadź trzecie prawo Kepplera dla orbit kołowych.

Rozwiązanie:

Początek formularza

Siła dośrodkowa F_d =

1.

2.

3.

4.

Siła grawitacji F_G =

1.

2.

3.

4.

Z porównania siły dośrodkowej i grawitacyjnej otrzymamy:

1.

2.

3.

4.

Stąd:

1.

2.

3.

4.

Dół formularza

Zadanie III-65

Na jakiej wysokości h nad Ziemią musi krążyć w płaszczyźnie równika satelita geostacjonarny?

Rozwiązanie:

Początek formularza

Siła grawitacyjna jest siłą dośrodkową:

1.

2.

3.

4.

Stąd odległość satelity od środka Ziemi R =

1.

2.

3.

4.

Oraz wysokość satelity nad Ziemią h =

1.
R

2.
R+R_Z

3.
R- 2R_Z

4.
R- R_Z

Co daje:

1.
3610⁶m

2.
6,410⁶m

3.
210⁶m

4.
3,810⁶m

Dół formularza

Zadanie III-66

Gwiazda podwójna składa się z dwóch obiektów o tej samej masie m znajdujących się w odległości d od siebie. Znając okres obrotu T wokół środka masy, znajdź masy gwiazd tworzących układ.

Rozwiązanie:

Początek formularza

Siła grawitacyjna F_G =

1.

2.

3.

4.

Siła dośrodkowa F_d =

1.

2.

3.

4.

Gdzie  =

1.

2.

3.

4.

Zatem masa każdej gwiazdy wynosi m =

1.

2.

3.

4.

Dół formularza

Zadanie III-67

Dwie identyczne sprężyny o stałej sprężystości k łączymy równolegle lub szeregowo. Ile wynoszą nowe stałe sprężystości k_r i k_sz odpowiednio w połączeniach równoległym i szeregowym?

Rozwiązanie:

Początek formularza

W połączeniu równoległym dodają się siły, F_Z =

1.

2.

3.

4.

Stąd k_r =

1.

2.
k

3.

4.

W połączeniu szeregowym dodają się wydłużenia x_sz =

1.

2.

3.

4.

Stąd k_sz =

1.

2.

3.

4.

Dół formularza

Zadanie III-68

Siła F_Z = 10 N rozciąga sprężynę zwiększając jej długość o x = 5 cm. Oblicz pracę W potrzebną do rozciągnięcia sprężyny o kolejne 5 cm.

Rozwiązanie:

Początek formularza

Stała sprężystości k =

1.

2.

3.

4.

Energia sprężystości wyraża się wzorem E_P =

1.

2.

3.

4.

Pracę liczymy z różnicy energii sprężystości W =

1.

2.

3.

4.

Co daje:

1.
1 J

2.
10 J

3.
5 J

4.
0,75 J

Dół formularza

Zadanie III-69

Oblicz energię całkowitą oscylatora harmonicznego o stałej sprężystości k.

Rozwiązanie:

Początek formularza

Dla oscylatora o równaniu
prędkość V =

1.

2.

3.

4.

Częstość oscylacji  =

1.

2.

3.

4.

Energia całkowita E_C =

1.

2.

3.

4.

Co daje:

1.

2.

3.

4.

Dół formularza

Zadanie III-70

Kulkę zawieszoną na nitce umieszczono w windzie. Porównaj okres wahań kulki w windzie stojącej i poruszającej się w dół z przyspieszeniem g/2.

Rozwiązanie:

Początek formularza

W windzie, poruszającej się z przyspieszeniem, działa siła bezwładności. Równanie ruchu kulki ma =

1.

2.

3.

4.

Czyli ma =

1.

2.

3.

4.

Jest to równanie wahadła, a odpowiadający mu okres to T =

1.

2.

3.

4.

Stosunek tego okresu, do okresu wahań kulki w windzie stojącej

1.
2

2.

3.

4.

Dół formularza

Zadanie III-71

Oblicz okres oscylacji T ciała puszczonego z powierzchni Ziemi i mogącego poruszać się swobodnie w tunelu przechodzącym przez jej środek. Porównaj ten okres z czasem obiegu satelity tuż przy powierzchni Ziemi.

Rozwiązanie:

Początek formularza

Siła grawitacyjna wewnątrz Ziemi F =

1.

2.

3.

4.
0

Jest to siła harmoniczna o stałej proporcjonalności k=-F/x

1.

2.

3.

4.

Okres oscylacji T =

1.

2.

3.

4.

Okres powyższy jest równy okresowi obiegu satelity T_S =
gdzie V₁ - pierwsza prędkość kosmiczna

1.

2.

3.

4.

Dół formularza

Zadanie III-72

Oblicz okres małych drgań wahadła matematycznego o długości l = 50 cm, umieszczonego w wagonie pociągu poruszającego się po poziomym torze z przyspieszeniem a_u = 4 m/s².

Rozwiązanie:

Początek formularza

Wagon pociągu jest układem nieinercjalnym, wiec na ciało działa siła bezwładności F_b=

1.

2.

3.

4.

Wartość efektywnego przyspieszenia działającego na ciało wynosi:

1.

2.

3.

4.

Zatem okres wahań T =

1.

2.

3.

4.

Co daje:

1.
0,5 s

2.
1,36 s

3.
3,14 s

4.
2,5 s

Dół formularza

Zadanie III-73

Jednorodny pręt o długości l został zawieszony na osi przechodzącej w odległości x powyżej jego środka masy. Dla jakiej odległości x okres tak otrzymanego wahadła jest najkrótszy?

Rozwiązanie:

Początek formularza

Moment bezwładności pręta obliczamy z twierdzenia Steinera I =

1.

2.

3.

4.

Okres takiego wahadła T =

1.

2.

3.

4.

Minimum okresu przypada na

1.

2.

3.

4.

Wtedy okres T =

1.

2.

3.

4.

33

---