Na dzisiejszych zajęciach będziemy szacować złożoność czasową algorytmów. Zwykle robi się to po to, by mieć pewność, czy te algorytmy wykonają się w jakimś tam określonym czasie. Nim jednak tego dokonamy warto przypomnieć definicję złożoności obliczeniowej. Złożoność obliczeniowa jest jednym z najważniejszych parametrów charakteryzujących algorytm. Decyduje on o efektywności całego programu. Podstawowymi zasobami systemowymi uwzględnianymi w analizie algorytmów są czas działania oraz obszar zajmowanej pamięci. Stad złożoność czasowa i złożonośc pamięciowa. Na złożoność czasową składają się trzy wartości: pesymistyczna, czyli taka, która charakteryzuje najgorszy przypadek działania oraz oczekiwana i średnia. Najczęściej algorytmy mają złożoność czasową proporcjonalną do funkcji:
lg(n) - Złożoność logarytmiczna (Pamiętając, że lg jest logarytmem o podstawie 2 a nie 10)
n - Złożoność liniowa
nlg(n) - Złożoność liniowo logarytmiczna
n2 - Złożoność kwadratowa
nk - Złożoność wielomianowa
2n - Złożoność wykładnicza
n! - Złożoność wykładnicza, ponieważ n!>2n już od n=4
Popatrzmy, jak te funkcje, a przynajmniej kilka z nich wyglądają na wykresie:
Niech f(n) na wykresie oznacza czas. Spośród wszystkich wymienionych złożoności można stwierdzić, że najlepszą z tych złożoności jest złożoność liniowa. Im bardziej zmierzamy w dół ku złożoności wykładniczej, tym gorszą mamy tą złożoność (algorytm nieefektywny). A teraz popatrzmy na taki przykład. Mamy dwie złożoności określone za pomocą nierówności: ![]()
. Jak widać z powyższych definicji, złożoność liniowa n jest bardziej efektywna. Jest jednak jedno ale - współczynniki przy n. Tu więc sytuacja nie będzie taka oczywista. Dla powyższej nierówności podzielmy obydwie strony przez 0,01 n. Wówczas otrzymamy coś takiego: ![]()
Stąd wniosek, ze w tym wypadku jeśli dane wejściowe byłyby mniejsze niż 10000, to szybciej powinno zostać wykonane zadanie algorytmem o zlożoności ![]()
. Z kolei jeżeli dane by były większe niż 10000, to wówczas miałoby sens zastosowanie algorytmu 0,01 n. I teraz oszacujmy zlożoność czasową takiego algorytmu. Załóżmy, że mamy tablice n elementową:
0 1 2 3 4 5 … n numery komórek
3 4 8 1 2 7 … wartości komórek
Powiedzmy, że algorytm polega tutaj na tym, że użytkownik wpisuje jedną z wartości komórek, a program w rezultacie ma zwrócić numer komórki w której wystapi ta wartość (przeszukuje tablicę od pierwszej komórki). Algorytm będzie miał postać pętli for tak jak niżej:
for (i=0; i<n; i++)
{
if tab[i]==szukana
return (i);
}
Mamy tu zatem do czynienia ze złozonością liniową - więc jedną z lepszych. I teraz jakie ten algorytm będzie posiadał złozoności czasowe? W najlepszym przypadku jeśli użytkownik poda wartość 3, to wówczas odczytana zostanie numer pierwszej komórki, czyli 0 i wówczas B(n) = 1. Z kolei w najgorszym przypadku jeśli użytkownik poda jakąś wartość poza tymi, co są, to wówczas z pierwszej komórki nastapi przeskok na drugą i tak dalej póki program nie natknie się na szukaną wartośc. I wówczas W(n) = n. W średnim przypadku z kolei A(n) w przybliżeniu będzie się równało ![]()
. Teraz kolejny z przykładów. Załóżmy, że mamy listę, w której wartości są uporządkowane powiedzmy rosnąco od 1 do 8:
1 2 3 4 5 6 7 8
Użytkownik wprowadza liczbę 8. I teraz załóżmy, że mamy algorytm, który wyszukuje w tej liście wartość wprowadzoną przez uzytkownika nastepującym sposobem. Na poczatek dzieli on listę na dwie części i patrzy jaka wartość wystepuje po lewej stronie. Jest to 4. Widzi, że 4 jest mniejsze od 8, stąd odrzuca wartości od 1 - 4 i poprzednia lista redukuje się do listy 5 6 7 8. Teraz znów dzieli powstałą listę na pół. Widzi, że 8 jest większe od 6. I tak algorytm ucina kolejny kawałek i redukuje listę jedynie do wartości 7 i 8. A że 7 jest mniejsze od 8, to algorytm potwierdza znalezienie ósemki. Jednak jego wykonanie zależy od tego, czy lista jest posortowana (niezależnie jednak od tego, czy rosnąco, czy malejąco). I tutaj mamy do czynienia ze złożonością czasową logarytmiczną. W najlepszym przypadku B(n) = 1, zaś w najgorszym - W(n) = lgn + 1. I jeszcze przykład algorytmu nieefektywnego. Dobrym przykładem jest algorytm ciągu Fibonacciego, który możemy rozpatrywać na dwa sposoby. Pierwszy jest liniowy o postaci:
0 1 2 3 4 5 … n numery komórek
1 1 2 5 8 13 … wartości komórek
Jego złożonośc czasowa wyniesie T(n) = n + 1. Z kolei w przypadku rekurencyjnym będziemy tworzyć nastepujące drzewo, gdzie dla każdego liścia będziemy korzystać ze wzoru ![]()
. A więc:
10
/ \
9
/ \ / \
6 7 7 8
…
I tak dalej. Tu widać wyraźnie, że będzie to sprawa nieco bardziej skomplikowana i szacuje się, że dla rekurencyjnie rozpatrzonego problemu złożoność czasowa wyniesie więcej niż ![]()
. Stąd ta nieefektywność. Przejdźmy teraz do nieco innego zagadnienia. Załóżmy, że mamy komputer, który wykonuje 1000 operacji na sekundę i mamy różne złożoności czasowe tych algorytmów: liniową, o potędze trzeciej i wykładniczą, czyli: ![]()
. I teraz pojawia się pytanie: W trakcie tej jednej sekundy jaki rozmiar danych jesteśmy w stanie wejściowym przetworzyć za pomocą tego algorytmu. Odpowiedź została przedstawiona w postaci tabeli:
T(n) |
1000 operacji na sekundę |
|
|
n |
1000 |
|
10 |
|
3 |
A teraz co jeśli komputer miałby moc obliczeniową równą milion operacji na sekundę. Tabela wówczas wyglądałaby następująco:
T(n) |
1000000 operacji na sekundę |
|
|
n |
1000000 |
|
100 |
|
6 |
Widać więc wyraźnie tą nieefektywność. Z kolei jeśli wyznaczymy jakąś funkcję złożoności określającą zlożoność czasową pewnego algorytmu, to dobrze byłoby, gdybyśmy mieli podać jakiego rzędu jest ta złozoność. Jeśli mamy na przykład funkcję o złożoności ![]()
, to aby określić rząd zlozoności wybieramy najgorszy element (w tym wypadku 2 do entej) i mówimy, że ta funkcja należy do rzędu równości teta od 2 do entej. Jednak to nasze oszacowanie trzebaby było udowodnić, że jest ono prawidłowe. Aby przeprowadzić dowód, potrzebne tu będzie pojęcie ograniczenia asymptotycznego górnego, które będziemy oznaczać literką O, oraz pojęcia ograniczenia asymptotycznego dolnego oznaczanego literką ![]()
. I wówczas jeżeli ![]()
, to ![]()
przy ![]()
. Teraz sprawdźmy, czy rzeczywiście ![]()
. A zatem niech ![]()
dla d = 2 (ze zbioru liczb rzeczywistych dodatnich). Ta funkcja ma ograniczać od góry ta funkcję złożoności g(n). Popatrzmy, jak by to wyglądało na wykresie:
Z kolei jeżeli ![]()
, to ![]()
przy ![]()
. I tu możnaby także sprawdzać, czy ![]()
. Wówczas by było ![]()
dla d = 1 (przykładowo). I teraz wykonajmy kilka przykładów praktycznych. Na początek takie zadanie. Należy napisać taki program (oraz obliczyć dla niego złożoności), który będzie zliczał w tablicy kwadratowej elementy oznaczone krzyżykami jak na poniższym rysunku:
Program będzie miał taką postać:
suma=0;
for(i=0;i<n;i++)
suma+=[0,i]+t[n-1,i];
for(i=1;i<n-1;i++)
suma+=t[i,n-1-i];
Tutaj złożonośc czasowa algorytmu T(n) = 1n + n - 2 = 3n - 2. I sprawdzamy jakiego rzedu jest ta funkcja. Będzie ona rzędu![]()
ograniczona w nastepujący sposób:
![]()
Teraz kolejne zadanie. Należy napisać taki program (oraz obliczyć dla niego złożoności), który będzie zliczał w tablicy kwadratowej elementy wszystkie z górnej części poza tymi, które są oznaczone krzyżykami jak na poniższym rysunku:
Program dla tego układu będzie miał postać:
for (i=0;i<n-1;i++)
{
for (j=1+i;j<n;j++)
suma+=t[i,j];
}
Mamy tu do czynienia z ciągiem o danym wzorze ![]()
z którego będziemy korzystali licząc złożoność czasową. I tak:
![]()
. Będzie ona rzędu ![]()
ograniczona w nastepujący sposób:
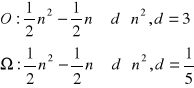
I ostatnie zadanie z tej serii. Należy napisać taki program (oraz obliczyć dla niego złożoności), który będzie zliczał w tablicy kwadratowej elementy brzegowe kwadratu ograniczone gwiazdkami (czyli wszystko co jest na zewnątrz ramki zagwiazdkowanej) jak na rysunku:
Program będzie wyglądał mniej więcej tak:
suma=0;
for(i=1;i<n-1;i++)
{
suma+=tab[1][i];
suma+=tab[n-2][i];
}
for (j=2;i<n-2;i++){
suma+=tab[i][1];
suma+=tab[i][n-2];
}
No i na koniec zlozoność. ![]()
. Będzie ona ograniczona następująco:
![]()
d * f(n)
g(n)
N
Wyszukiwarka