RACHUNEK RÓŻNICZKOWY FUNKCJI JEDNEJ ZMIENNEJ.

Definicja. Jeżeli iloraz różnicowy
funkcji f w punkcie a ma granicę przy
, to granicę tę oznaczamy przez
i nazywamy pochodną funkcji f w punkcie a.

.

Uwagi. Jeśli
to
.

5. Pochodna funkcji
(n- liczba naturalna):

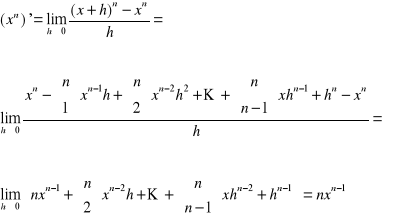
( wzór wdumienny Newtona).

Zatem
.

Interpretacja geometryczna pochodnej

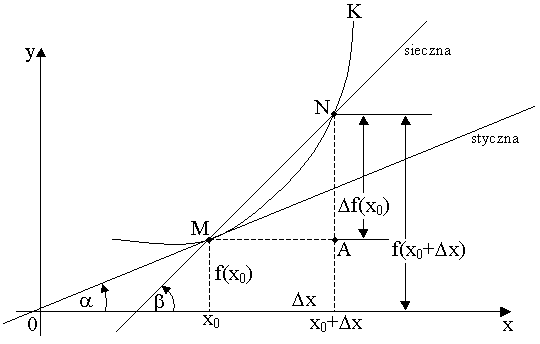
Jeśli
, to
i
. Z drugiej strony
. Zatem
, czyli pochodna w punkcie równa się tangensowi kąta nachylenia stycznej w tym punkcie.

Definicja. Styczną do krzywej o równaniu
w danym punkcie
nazywamy

prostą przechodzącą przez ten punkt, której współczynnik kierunkowy jest równy
. Normalna do krzywej f w punkcie a jest to prosta prostopadła do stycznej w tym punkcie i przechodząca przez punkt styczności.

Uwagi. Jeżeli
jest kątem nachylenia stycznej do osi OX, to
. Równanie stycznej w punkcie a ma zatem postać

,

zaś równanie normalnej

.

Podstawowe twierdzenia o pochodnej

Definicja. Pochodną prawostronną /lewostronną/ funkcji f w punkcie a nazywamy skończoną granicę
/
/. Prostą o równaniu
/
/ nazywamy styczną lewostronną /prawostronną/ do krzywej
.

Przykłady. Rozpatrzmy funkcję
. Jej iloraz różnicowy w punkcie
wynosi

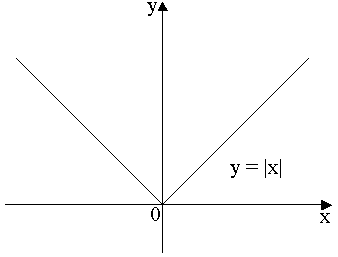
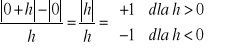
Iloraz ten nie ma granicy gdy
, istnieje natomiast granica prawostronna równa 1 i lewostronna równa -1.

Funkcja
nie ma więc pochodnej w punkcie
, ma zaś w tym punkcie pochodną prawostronną równą 1 i lewostronną równą -1.W punkcie
krzywa będąca wykresem tej funkcjj nie ma stycznej, natomiast istnieje styczna lewostronna (o równaniu
) i styczna prawostronna o równaniu
.

Twierdzenie. Jeśli funkcja jest różniczkowalna w danym punkcie, to jest w nim ciągła.

Dowód. Załóżmy, że funkcja f jest różniczkowalna w punkcie x. Wówczas
. KD.

Uwagi. Twierdzenie odwrotne jest fałszywe (patrz przykład wyżej).

Twierdzenie. Jeśli funkcje u i v są różniczkowalne w a, to istnieją pochodne sumy, różnicy, iloczynu i ilorazu funkcji u i v w punkcie a i są one równe odpowiednio:

.

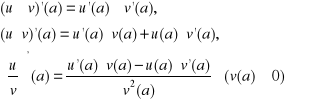
Dowód (dla ilorazu funkcji). Ponieważ
,

zatem

.

Wykorzystaliśmy tu definicję iloczynu funkcji i fakt, że istnieją pochodne
, a zatem funkcje u i v są ciągłe w a. KD.

Twierdzenie (O pochodnej funkcji złożonej). Jeżeli funkcja
ma pochodną w punkcie
równą
, a funkcja
ma pochodną
w punkcie
, to funkcja złożona
ma pochodną w punkcie
równą
.

Uwaga. Krótko (lecz nieprecyzyjnie):
.

Dowód. Niech
. Jeśli
, to kolejno:
(istnieje
, więc g jest w
ciągła).

Z założeń wynika więc, że:

. KD.

Definicja. Funkcją wykładniczo-logarytmiczną nazywamy funkcję postaci
.

Przykłady.

1. Niech
. Wówczas
,

czyli
.

Twierdzenie (O pochodnej funkcji odwrotnej). Jeśli
i dla funkcji
istnieje funkcja odwrotna
oraz
, to

i
.

Uwagi. Krótko:
.

Dowód. Mamy
. Zatem

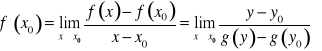
. Ponieważ funkcja g jest ciągła w punkcie
(bo ma w nim pochodną), a tym samym funkcja f jest ciągła w punkcie
, więc
. Zatem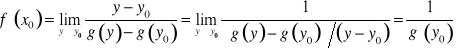
. KD.

Przykłady.

1. Znając pochodną funkcji wykładniczej, obliczymy pochodną funkcji logarytmicznej

Ponieważ
oraz
więc
.

Funkcje Cyklometryczne

1.
.

Oczywiście
. Ponieważ
tylko dla
, więc musimy się ograniczyć do przedziału otwartego
. Dla
otrzymujemy
.

Zatem
i pochodna ta istnieje dla
.

2.
.

Mamy tu
oraz
dla
, a więc też należy się ograniczyć do przedziału
. Ponieważ
(bo
dla
), więc
.

Zatem
.

3.
.

Ponieważ
, więc
, skąd
.

Zatem
.

4.
.

Ponieważ
, więc
, skąd
.

Zatem
.

Różniczka zupełna

.

Twierdzenie. Jeśli istnieje
, to funkcja f posiada różniczkę w a.

.

Wniosek. Dla małych h wyrażenie
szybko zmierza do 0, skąd dostajemy tzw. przybliżony wzór z różniczką :
.

Pochodne wyższych rzędów

Definicja. Pochodną n-tego rzędu z funkcji f nazywamy pochodną z jej
-szej pochodnej (jeżeli istnieje), czyli:
oraz
.

Definicja. Klasa
jest to zbiór wszystkich funkcji określonych na
, które posiadają n-tą pochodną ciągłą w
(a zatem także wszystkie pochodne niższych rzędów ciągłe w
). Klasa
jest to zbiór wszystkich funkcji określonych na
, które posiadają n-tą pochodną ciągłą w
i ciągłą prawostronnie w a i ciągłą lewostronnie w b.

Uwagi. Zatem
jest zbiorem wszystkich funkcji ciągłych w
.

4. Wzór Leibniza.

Niech
, gdzie u i v są funkcjami zmiennej x n-krotnie różniczkowalnymi.

Mamy wówczas

.

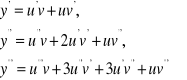
Metodą indukcji matematycznej można udowodnić następujący Wzór Leibniza:

,

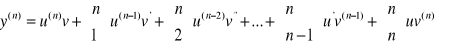
czyli krótko

.

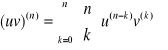
Zwróćmy uwagę na analogię między wzorem Leibniza i wzorem dwumiennym Newtona.

Twierdzenie Rolle'a. Jeśli
i jest różniczkowalna w
oraz
, to istnieje taki punkt
, w którym
.

Dowód. Rozpatrzmy dwa przypadki.

1.
. Wówczas twierdzenie jest oczywiste, gdyż
w całym przedziale.

2.
. Wiadomo (tw. Weiertrassa), że funkcja ciągła w
przyjmuje zarówno wartość największą, jak i najmniejszą, a więc istnieje w tym przedziale taki punkt, w którym wartość funkcji jest największa, oraz istnieje taki punkt, w którym wartość funkcji jest najmniejsza. Ponieważ
, więc przynajmniej jeden z tych punktów musi leżeć wewnątrz przedziału, gdyż w przeciwnym razie funkcja byłaby stała. Oznaczamy ten punkt przez
i przypuśćmy, że funkcja przyjmuje w nim wartość największą. Wtedy dla wszystkich innych
mamy
, czyli
. Dzieląc tę nierówność obustronnie przez
otrzymujemy

(1)
.

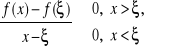
Ponieważ funkcja f jest różniczkowalna w
, więc przy
mamy
.

Z zależności (1) wynika, że
oraz
, co jest możliwe tylko wówczas, gdy
. KD.

Twierdzenie (Lagrange'a). Jeśli
i jest różniczkowalna w
, to istnieje taki punkt
, w którym
.

Uwagi. Twierdzenie Rolle'a jest szczególnym przypadkiem twierdzenia Lagrange'a: dla
otrzymujemy bowiem
.

Dowód. Rozpatrzmy funkcję pomocniczą
.

Funkcja
spełnia wszystkie założenia twierdzenia Rolle'a: jest ciągła i różniczkowalna tam gdzie f oraz
. Istnieje wobec tego taki punkt
, że
oraz
. Ale

, a więc
skąd otrzymujemy tezę twierdzenia. KD.

Wniosek: Jeśli f spełnia założenia tw. Lagrange'a, to
.

Twierdzenie. Funkcja jest stała wtedy i tylko wtedy gdy jej pochodna jest zerowa, czyli:
w
.

Dowód. Niech
oznaczają dwa dowolne punkty danego przedziału. Wówczas

, bo
. Zatem
, co wobec dowolności punktów
oznacza, że funkcja jest stała. KD.

Przykłady. Stosując to twierdzenia wykażemy znany już związek
.

Ponieważ
, więc
.

Obliczamy jeszcze
i to kończy dowód.

Twierdzenie. Jeżeli
, jest różniczkowalna w
i
w
/
w
/, to
w
/
w
/.

Dowód. Niech
oznaczają dowolne punkty danego przedziału i
w
. Wówczas
i
, a zatem
. To zaś oznacza, że
w
. Podobnie udowadnia się twierdzenie dla funkcji malejącej. KD

Przykłady.

1. Udowodnić, że
.

Otóż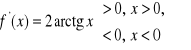

a więc
w
/
w
/. Ponieważ
, więc mamy
, a zatem rozważana nierówność jest prawdziwa.

2. Niech
. Mamy
, zatem
w
. Ponieważ
, więc w przedziale
znajduje się pierwiastek równania
i jest to jedyny pierwiastek tego równania.

Twierdzenie (Taylora). Jeżeli w
istnieje
, to dla każdego
istnieje takie c, że

,

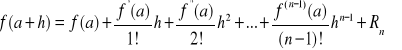
gdzie
nazywamy resztą Lagrange'a, a c jest nieznanym punktem pośrednim leżącym między
.

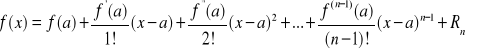
Wzór Taylora w punkcie
nazywamy wzorem Maclaurina:

(9)

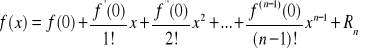
Zauważmy, że jeśli wszystkie pochodne
są ograniczone przez wspólną stałą i
, to mamy
. Zatem jest sens opuścić resztę
w (9). Dostajemy wówczas tzw. przybliżony wzór Taylora:

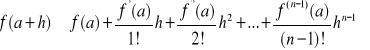
, którego błąd bezwzględny wynosi
.

Przykłady.

2. Uporządkujemy wielomian
według potęg
. Ponieważ

,

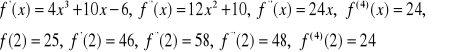
więc

i ostatecznie
.

3. Dla funkcji
mamy
.

Zatem wzór Maclaurina dla tej funkcji ma postać

,

a wzór przybliżony

.

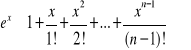
Dla
dostajemy stąd wzór na obliczanie przybliżonych wartości liczby

.

Ponieważ
, więc
i
. Zatem błąd przybliżenia jest mniejszy od
. Aby uzyskać np. dokładność do pięciu miejsc dziesiętnych, tzn. aby błąd nie przekraczał pięciu jednostek szóstego miejsca dziesiętnego, trzeba uwzględnić we wzorze tyle wyrazów, żeby
. Najmniejsze n spełniające tą nierówność wynosi 10. Mamy więc

Twierdzenie (Hospitala). Załóżmy, że funkcje
i
są różniczkowalne w
,
, istnieje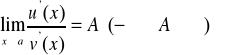
. Wówczas istnieje
.

Uwagi. Twierdzenie to pozostaje prawdziwe dla granic jednostronnych i granic w
.

Przykłady.

4. Może się zdarzyć, że stosowanie reguły de l'Hopitala nie daje rezultatu. Łatwo obliczamy, że
, ale iloraz pochodnych
nie ma granicy w punkcie 0.

Wyrażenie nieoznaczone
przekształcamy do postaci
lub
stosując wzory
lub
.

Przykłady.
.

Wyrażenie nieoznaczone
przekształcamy do postaci
lub
stosując wzór
.

Ekstrema funkcji jednej zmiennej.

Definicja. Mówimy że funkcja
ma w punkcie
silne minimum /maksimum/ lokalne (krótko: min /max/), jeżeli istnieje
takie, że
/
/ dla każdego x z
.

Twierdzenie. Jeżeli funkcja
ciągła w
oraz różniczkowalna w
, ma tę własność, że
dla
i
dla
/
dla
i
dla
/, to
ma w punkcie
maksimum.

Dowód. Z założenia wynika, że funkcja
jest rosnąca na lewo, a malejąca na prawo od punktu a, czyli
dla
oraz
dla
.

Zatem - zgodnie z definicją - w punkcie a istnieje maksimum. KD.

2. Funkcja
jest wszędzie ciągła,
, natomiast nie ma pochodnej w punkcie 0 (ZD). Stwierdzamy, że
dla
oraz
dla
, a więc w punkcie 0 funkcja ma minimum. Wykresem tej funkcji jest tzw. parabola Neila.

Twierdzenie. Jeśli f jest różniczkowalna w
i f ma ekstremum w a, to .
(Warunkiem koniecznym dla istnienia ekstremum funkcji w punkcie a jest zerowanie się pierwszej pochodnej w tym punkcie).

Definicja. Jeśli
, to a jest punktem stacjonarnym.

Twierdzenie. Jeżeli funkcja
ma pierwszą i drugą pochodną ciągłą w
oraz jeżeli
i
to w punkcie a funkcja
osiąga ekstremum: minimum gdy
, a maksimum gdy
.

Dowód. Załóżmy, że
. Wówczas wzór Taylora w punkcie a dla
ma postać
, gdzie c leży między x i a. Ponieważ
, więc
. Wobec ciągłości drugiej pochodnej,
i
mają takie same znaki (gdy x jest dostatecznie blisko a). Zatem dla
mamy
, a więc
osiąga minimum, natomiast dla
mamy
, a zatem
osiąga maksimum. KD.

Przykłady. Znajdziemy ekstrema funkcji
.

Obliczamy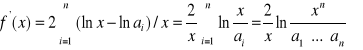
.

Rozwiązując równanie
, otrzymujemy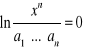
, skąd znajdujemy punkt stacjonarny
(średnia geometryczna liczb
).

Ponieważ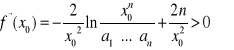
, więc w punkcie
mamy minimum.

Wypukłość, punkty przegięcia.

Definicja. Funkcja (krzywa) f jest wypukła w górę /dół/ w
wtedy i tylko wtedy, gdy dla każdych
odcinek otwarty
leży poniżej /powyżej/ tej krzywej.

Uwagi. Jeśli f jest wypukła w górę /dół/ w
, to piszemy
w
/
w

/.

Dla funkcji f wypukłej w górę /dół/ w
podczas poruszania się z punktem x od a do b współczynniki kierunkowe stycznej do f w punkcie x maleją /rosną/, a zatem prawdziwe jest

Twierdzenie. Jeżeli funkcja
jest różniczkowalna w
, to
/
/.

Twierdzenie. Jeżeli f jest dwukrotnie różniczkowalna w
, to
/
/.

Dowód. Istotnie, jeżeli np.
to
, a zatem
. KD.

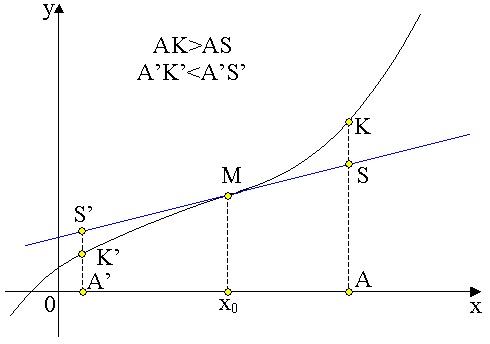
Kolejne przedziały wypukłości w górę i w dół danej krzywej ciągłej ograniczone są punktami przegięcia. Punkt przegięcia krzywej (funkcji) jest to więc jej punkt ciągłości, w którym wypukłość w górę przechodzi w wypukłość w dół i odwrotnie. Jeżeli w punkcie przegięcia istnieje styczna, to krzywa w tym punkcie przechodzi z jednej strony stycznej na drugą.

Twierdzenie. Jeżeli funkcja f jest dwukrotnie różniczkowalna w
i ma drugą pochodną zmieniającą znak w punkcie a, to a jest punktem przegięcia. Jeżeli ponadto
jest ciągła w a, to
. Zerowanie się drugiej pochodnej jest zatem warunkiem koniecznym dla istnienia przegięcia.

Asymptoty pochyłe

Definicja. Prosta o równaniu
jest asymptotą pochyłą w
/
/ krzywej f, jeżeli

(1)
.

Jeśli ma miejsce (1) to również
, czyli
. Ponieważ
, więc
, czyli
. Dokładniej:

i
.

Korzystając z (1)wyznaczamy b:

i
.

Przybliżone metody rozwiązywania równania
.

Zaprezentujemy teraz dwie metody numerycznego (czyli przybliżonego) obliczania pierwiastka
równania

(2.2)
dla
.

1. Metoda bisekcji. Była już prezentowana podczas dowodu tw. Bolzano-Cauchy'ego.

Załóżmy, że spełnione są założenia tego twierdzenia, a w szczególności
. Startujemy z
i każde następne przybliżenie obliczamy ze wzoru
, gdzie przedziały
są tak wybrane, że
. Wówczas wiadomo z tw. Bolzano-Cauchy'ego, że
, czyli ciąg kolejnych przybliżeń (iteracji) zmierza do pierwiastka równania (2.2). Metoda bisekcji jest jedną z wielu metod przybliżonych (iteracyjnych). Można zdefiniować rząd (szybkość) zbieżności takiej metody: im większy rząd tym większa szybkość metody. Dowodzi się, że metoda bisekcji ma rząd 1.

Znacznie szybsza jest omówiona niżej metoda Newtona (rząd zbieżności = 2).

2. Metoda Newtona (stycznych).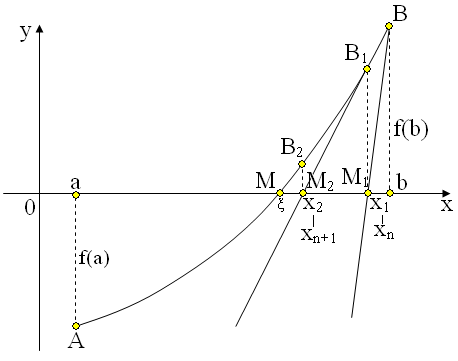

W metodzie tej startujemy od dowolnego punktu startowego
, w którym znajdujemy styczną do
. Punkt przecięcia tej stycznej z OX jest następnym przybliżeniem
. W punkcie
znowu znajdujemy styczną do
itd.

Równanie stycznej w

. Dla
mamy
, skąd wynika wzór na n-tą iterację metody Newtona:
,
-dowolny punkt startowy.

Dla oszacowania błędu jakim obarczone jest n-te przybliżenie
rozwińmy funkcję
według wzoru Taylora dla przedziału
, gdzie
- pierwiastek równania (2.2):

, gdzie c leży między
i
.

Ponieważ
, więc
.

Dzieląc obie strony przez
otrzymujemy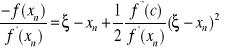
.

Ale
, skąd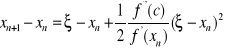
,

czyli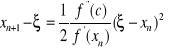
. A zatem

(99)
,

gdzie
,
.

Widzimy więc, że przy metodzie Newtona każde następne przybliżenie daje błąd nie większy od kwadratu błędu poprzedniego przybliżenia (pomnożonego przez stałą
). Wzór (99) oznacza, że metoda Newtona ma rząd 2 czyli jest szybko zbieżna. Przyjmując dla uproszczenia stałą
zauważmy, że jeśli przybliżenie
obliczono z dokładnością np. 0.1 (czyli
), to
.

Zatem już czwarta iteracja daje aż osiem cyfr dokładnych pierwiastka
!

Przykłady.

1. Zbadać funkcję
.

a) Dziedzina.
. W punkcie 0 funkcja nie jest określona, ale z tw. Hospitala obliczamy
.

b) Funkcja przyjmuje następujące wartości:

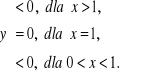
c) Ponieważ funkcja jest w całej dziedzinie ciągła, nie ma więc asymptot pionowych. Obliczamy granice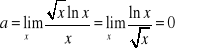
oraz
,

zatem funkcja nie posiada asymptot ukośnych.

d) Pochodna
,

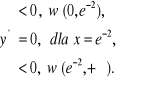
Ponadto
. Zatem
,
, w
jest minimum i
.

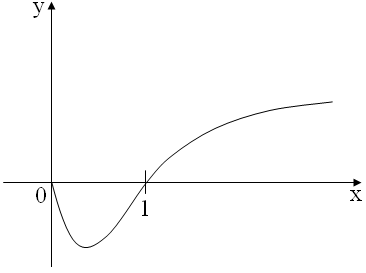
e) Ponieważ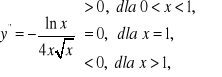

więc
,
, a w punkcie
ma przegięcie. Współczynnik kierunkowy stycznej w punkcie przegięcia wynosi
. Wykres funkcji przedstawiono na rys. ??.

2. Zbadać funkcję
.

a)
, a więc
.

b) Funkcja przyjmuje tylko wartości dodatnie.

c)

d)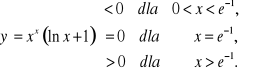

Z wartości granicy
wynika, że krzywa zbliża się do punktu
pod kątem

Ponadto z zastosowania (1.3) wynika, że
,
, a więc w punkcie
ma minimum równe

e) Krzywa nie ma asymptot, bo wszędzie jest ciągła oraz

f)
, ponieważ zawsze
.

---