1. Wprowadzenie - powtorka algorytmizacji

- operacje notacje pseudo kod, sieć działań,

- zmienna prosta z adresem i indeksowana jedno i dwuwymiarowa

- proste algorytmy dla zmiennej prostej i indeksowanej ( suma, szereg, maksimum )

2 Przekształcanie algorytmów złożone zastosowania instrukcji pętli i warunków

- algorytm pętli ze skokiem bezwarunkowym i przekształcenie na while i 3x do

- warunek złożony z optymalizacją pamięci (wytyczne dla alpinisty tlen w górach )

3 Algorytmy symulacji obliczeń iteracyjnych analiza i synteza algorytmur

- warunek rozmnażania komówek p(i)=2ⁱ i f(i) = f(i-1) +2*f(i-2)

- zliczanie wyrazów ( znaki czytane na bieżąco)

4 Histogram

- w wersji po posortowaniu

- bez sortowania

5 Sortowanie bąbelkowe

6 Marsz

- w układzie kartezjanskim

- w układzie biegunowym

7 Sortowanie przez wstawianie

8 Sortowanie przez wybór

9 Symulacja układu dynamicznego

I-go i II-go rzędu

10 Rekurencja

silnia wypiszcyfry, symbol newtona

11 Rekurencja

rownanie

13 Rekurencja

QuickSort

14 Reprezentacja danych (powt tablic stat dynam i struktury )

15 Dane Wyszukiwanie wzorca

1a Symbole algorytmu graficznego Sieć działań

1b Pamięć

zmienne

proste złożone (tablice)

ciąg, tablica jednowymiarowa

_{i = 1 2 3 4 5 6}

A

23.4

0.0

4.0

4.54

1.2e3

25.4

a_i a₁ a₂ a₃ a₄ a₅ a₆

struktura dane w tablicy struktur

Element
id	X	Y	txt	pE
1	10.2	23.03	„elit”	1233330
2	20.0	45.20	„e1b”	1233385
5	30.1	73.02	„12a”	0
...	...

E

1.c)

Oblicz sumę wartości podawanych z klawiatury

(załóż różne warunki zakończenia obliczeń

- podania wyniku)

1.d)

Dana tablica n całkowitych elementów .

algorytm obliczania maksimum z tych elementów

1.e)

Dana liczba rzeczywista x oraz liczba całkowita n ≥ 0

algorytm obliczania y = xⁿ

1.f)

Dana liczba rzeczywista x oraz liczba całkowita n ≥ 0

Oblicz sumę 1/xⁱ dla i = 0,1,2 ... n

2 Przekształcanie algorytmów złożone zastosowania

instrukcji pętli i warunków

- algorytm pętli ze skokiem bezwar i przekształcenie na while i 3x do

2a) Dany jest ogólny iteracyjny algorytm. Utwórz równoważne algorytmy, w których występuje pętla

a) z warunkiem na wejściu do pętli ( dopóki, while)

b) z warunkiem na wyjściu z pętli (powtarzaj repeat)

Uwaga: instrukcje X i Y nie zmieniają wartości n

ale mogą od niej zależeć.

void PetlaGoTo()

{ int i=0, n = NN; double x ,y; x =XX, y = YY;

pocz:

x = x + 1 + y + n + i; // instr X

if (n > 0) {

i = i + 1;

y = x + y - 1 - n - 2 * i; // instr Y

n = n - 1;

goto pocz;

}

printf ("\n\tPetla GoTo\t % .......lf\n",i,n,x,y);

}

po2b - warunek złożony z optymalizacją pamięci (wytyczne dla alpinisty tlen w górach )

2b) Dana jest lista nazw i wysokości h górskich szczytów Podaj algorytm, który wypisuje na ekranie informację

------------------|------------------------|------------------------>

6 8 h[tyś m]

„wejscie” „wejscie z tlenem” „nie wchodz”

Wyniki

int main() { printf ("start\n");

PetlaGoTo();

PetlaWhile();

PetlaDoA(); PetlaDoB(); PetlaDoc();

getchar();

}

/*

Petla Go To 5 0 1042.0 631.0

Petla While 5 0 1042.0 631.0

Petla Do vA 5 0 1042.0 631.0

Petla Do vB 5 0 1042.0 631.0

*/

ro2

// Rozwiazania

#include <math.h>

#include <stdio.h>

#define XX 4

#define YY 4

//#define NN 0

//#define NN -5

//#define NN 5

/* Zad ASDRozPetle

2a. Dla danego ogólnego iteracyjnego algorytmu utwórz równoważny program, w których wyeliminujesz skok bezwarunkowy

- zastepując go pętlą while (warunek) instrukcja

- zastepując go pętlą do instrukcja while (warunek)

Uwaga: instrukcje 1 i 2 mogą wzajemnie od siebie zależeć i nie zmieniając wartości n mogą od niej zależeć.

*/

void PetlaGoTo() {

int i=0, n = NN; double x ,y; x =XX, y = YY;

pocz:

x = x + 1 + y + n + i;

if (n > 0) {

i = i + 1;

y = x + y - 1 - n - 2 * i;

n = n - 1;

goto pocz;

}

}

/* ------------------------------------------------/*

void RPetlaWhile() {

int i=0, n =NN; double x ,y; x = XX, y = YY;

x = x + 1 + y + n + i;

while (n>0){

i = i + 1;

y = x + y - 1 - n - 2 * i;

n = n - 1;

x = x + 1 + y + n + i;

}

}

/* ------------------------------------------------/*

void RPetlaDoA() {

int i=0, n = NN; double x ,y; x = XX, y = YY;

x = x + 1 + y + n + i;

do {

if (n <= 0) break; // LUB if (n > 0)

i = i + 1;

y = x + y - 1 - n - 2 * i;

n = n - 1;

x = x + 1 + y + n + i;

}while (n>0);

}

/* ------------------------------------------------/*

void RPetlaDoB() {

int i=0, n = NN; double x ,y; x = XX, y = YY;

do {

if (n <= 0) break; // LUB if (n > 0)

x = x + 1 + y + n + i;

i = i + 1;

y = x + y - 1 - n - 2 * i;

n = n - 1;

}while (n>0);

x = x + 1 + y + n + i;

}

void RPetlaDoC() {

int i=0, n = NN; double x ,y; x = XX, y = YY;

if (n > 0)

do {

x = x + 1 + y + n + i;

i = i + 1;

y = x + y - 1 - n - 2 * i;

n = n - 1;

}

while (n>0);

x = x + 1 + y + n + i;

}

/* ------------------------------------------------/*

void RPetlaDoD() {

int i=0, n = NN; double x ,y; x = XX, y = YY;

do {

x = x + 1 + y + n + i;

i = i + 1; // printf ("s%10.4lf %10.4lf %10d\n",y,t,i);

y = x + y - 1 - n - 2 * i;

n = n - 1;

}

while (n>0);

if (n < 0)

x = x + 1 + y + n + i;

printf ("\n\tPetla Do vD\t%10d \

%10d%10.4lf%10.4lf\n",i,n,x,y);

}

int main()

{

printf ("ROZWIAZANE TESTY WYNIKOW\n" );

PetlaGoTo();

RPetlaWhile();

RPetlaDoA();

RPetlaDoB();

RPetlaDoC();

}

start

Petla Go To 5 0 1042.0 631.0

ROZWIAZANE TESTY WYNIKOW

Petla While 5 0 1042.0 631.0

Petla Do vA 5 0 1042.0 631.0

Petla Do vB 5 0 1042.0 631.0

Petla Do vC 5 0 1042.0 631.0

Petla Go To 0 0 9.0 4.0

ROZWIAZANE TESTY WYNIKOW

Petla Go To 0 0 9.0 4.0

Petla While 0 0 9.0 4.0

Petla Do vA 0 0 9.0 4.0

Petla Do vB 0 0 9.0 4.0

Petla Do vC 0 0 9.0 4.0

Petla Go To 0 -5 4.0 4.0

ROZWIAZANE TESTY WYNIKOW

Petla Go To 0 -5 4.0 4.0

Petla While 0 -5 4.0 4.0

Petla Do vA 0 -5 4.0 4.0

Petla Do vB 0 -5 4.0 4.0

Petla Do vC 0 -5 4.0 4.0

*/

po3

3 Algorytmy symulacji obliczeń iteracyjnych analiza i synteza algorytmu

3a - warunek rozmnażania komówek p(i)=2ⁱ i f(i) = f(i-1) +2*f(i-2)

- zliczanie wyrazów ( znaki czytane na bieżąco)

po3b

3b zlicz ilość wyrazów z bieżąco czytanych znaków

- zliczanie wyrazów ( znaki czytane na bieżąco)

1111111

01234567890123456

Ula⋅ma⋅psiaka

Ula⋅⋅⋅⋅ma⋅⋅⋅⋅⋅⋅psiaka

⋅⋅⋅⋅⋅⋅Ula⋅⋅⋅⋅⋅⋅⋅ma⋅⋅⋅psiaka⋅⋅⋅

⋅Ula⋅⋅ma⋅⋅⋅psiaka⋅⋅⋅

ro3

Jeśli wystąpiła 2 znakowa sekwencja

spacja i znak różny od spacji

to zwiększany jest licznik wyrazów k

Wyrazy rozdzielone są conajmniej jednym odstępem

k - licznik wyrazów , b - znak bieżący, p - znak poprzedni

#include <conio.h>

#include <stdio.h>

int main()

{

int p=' ',b,k=0;

while((b=getch()) >=' ')

{

if( b != ' ' && p == ' ') k++ ;

p = b;

}

printf("%d\n",k);

}

Uwaga: Testy w/w algorytmu wygodniej jest przeprowadzać na tablicy np:

#include <conio.h>

#include <stdio.h>

int main()

{

static char t[80]=" Ula ma psiaka ";

char p=' ',b, *pt=t; int k=0;

while( b = *pt++ ) {

if( b != ' ' && p == ' ') k++ ;

p = b;

}

printf("%d\n",k);

}

4 Histogram po4

program histogr;

const NH=13;

{ Dany wektor zawiera zbior powtarzajacych sie elementów

Program oblicza wektor, b ktory jest podzbiorem wszystkich elementów wektora a oraz wektor c okreslajacy liczbe ich wystąpien w wektorze a

i 1 2 3 4 5 6 7 8 9 10

-----------------------------------------------------------

a[i] 3 5 2 5 1 7 6 5 7 1

b[i] 3 5 2 1 7 6

c[i] 1 3 1 2 2 1

}

type wek = array[1.. NH] of integer;

const a:wek= (3,5,2,5,1,7,6,5,7,1,10,14,5);

var

b,c:wek;

k,n,i,kmax:integer;

nw:boolean;

BEGIN

kmax := 10;

/* ------------------------------------------------/*

{ z goto }

BEGIN

kmax := 10; c[1]:=1;

n := 1;

b[1] := a[1];

FOR k := 2 TO kmax DO BEGIN

j := 1;

new:

IF ( b[j] = a[k] ) THEN

c[j] := c[j] + 1

ELSE BEGIN

j := j+1;

if ( j <= n ) THEN

goto new

else begin

n := n + 1;

c[n] := 1;

b[j] := a[k];

end

END

END;

/* ------------------------------------------------/*

n := 0; 2 x FOR z flagą nw

FOR k := 1 TO kmax DO BEGIN

nw := true;

FOR i := 1 TO n DO

IF ( b[i] = a[k] ) THEN begin

nw := false;

c[i] := c[i] + 1;

break;

end;

IF nw THEN begin

n := n + 1;

c[n] := 1;

b[n] := a[k];

end;

END;

{ wydruki dla k := 1..n b[k], c[k] ; }

END.

#include <stdio.h>

#define NHIST 11

int main() {

static int a[NHIST]= {3, 5, 2, 5, 1, 7, 6, 5, 7, 1},

b[NHIST], c[NHIST];

int k,n=0,j,nw,kmax = 10;

//for (k = 0; k<kmax; k++ ) { c[k]=b[k]=-10;}

//łapanie błędów obliczeniowych

n = 0;

for (k = 0; k<kmax; k++ ) {

for(j = 0, nw++ ; j < n ;j++ )

if (a[k] == b[j]) {

nw=0;

c[j]=c[j]+1;

break;

}

/* j = 0, nw++ ;

do if (a[k] == b[j]) {

nw = 0; c[j]=c[j]+1; break; }

while (j++ < n); */

/* while (j++ < n) if (a[k] == b[j]) {

nw = 0; c[j]=c[j]+1; break;

} */

if (nw) {

c[n]=1;

b[n++]=a[k];

}

} // end for k

for(k = 1; k<=kmax; k++ ) printf("%4d",k); printf("\n");

for(k = 0; k<kmax; k++ ) printf("%4d",a[k]); printf("\n");

for(k = 0; k<n; k++ ) printf("%4d",b[k]); printf("\n");

for(k = 0; k<n; k++ ) printf("%4d",c[k]); printf("\n");

return 0;

}

{ z goto }

BEGIN

kmax := 10; c[1]:=1;

i := 1;

b[1] := a[1];

FOR k := 2 TO kmax DO

BEGIN

j := 1;

new:

IF ( b[j] = a[k] ) THEN

c[j] := c[j] + 1

ELSE BEGIN

j := j+1;

if ( j <= i ) THEN

goto new

else begin

i := i + 1;

c[i] := 1;

b[j] := a[k];

end

END

END;

ko4

5 Sortowanie bąbelkowe po5 SrtBabF.c

//5a Sortowanie bąbelkowe z FOR

// Posortuj n element. tablicę w porządku rosnącym

// za pomocą metody sortowania bąbelkowego

#include <stdio.h>

#include <stdlib.h>

int main(void) {

static int v[] = { 8, 3, 5, 7, 1, 4, 10, 9}; // testujący 25

//static int v[] = {1,4,3,5,7,8,9,10}; // prawie uporzadkowany 13

//static int v[] = {1,3,4,5,7,8,9,10}; // uporzadkowany 7

// static int v[] = {10,9,8,7,5,4,3,1}; // malejący 28

int k=0,tmp,przest,i,j, n=8;

printf("Sortownie babelkowe - ciag niesortowany\n");

for (i=0;i < n; i++) printf("%3d", v[i]); printf("\n");

/* Petla zewnetrzna jest wykonywana raz dla kazdego kolejnego elementu tablicy

dokonujac podzialu na czesc posortowana i nieposortowana.

W kazdej wewnetrznej iteracji sąsiednie elementy zostaną zamienione zgodnie

z załozoną kolejnością sortowania a aktualny największy element jest ustawiony

na koncu nieposortowanej cześci ciagu i nie bedzie brany pod uwage

w nastepnych iteracjach */

przest = 1;

for (i = 0; i < n && przest; i++) // ?? CZY WYRZUCIC i<n

{ /* Jezeli na koncu iteracji widzimy, ze nie zostala wykonana zadna zamiana to oznacza, ze lista jest juz posortowana i koniec iteracji. */

przest = 0; // n = n -1

for (j = 0; j < n - 1 - i; j++, k++) // for (j = 0; j < n - 1; j++) //

if ( v[j] > v[j+1] ) { //gdy v_j > v_j+1 .

tmp = v[j]; // to nieodpowiednia kolejnosć.

v[j] = v[j+1]; // więc zamiana.

v[j+1] = tmp;

przest=1; // zapamietaj fakt zamiany

} // testy

}

.................

}

Ciag niesortowany 8 3 5 7 1 4 10 9

Ciag rosnaco posortowany 1 3 4 5 7 8 9 10

//5b Sortowanie bąbelkowe z DO WHILE

int main(void) {

static int v[] = {8,3,5,7,1,4,10,6};

int k,tmp,przest,i,j, n= 8, n0; n0 = n;

printf("Sortownie babelkowe - ciag niesortowany\n");

i=0; while(i < n) { printf("%3d", v[i]); i=i+1; } printf("\n");

do {

przest = 0;

j = 0;

n = n - 1;

while (j < n) {

if ( v[j] > v[j+1] ) {

tmp = v[j];

v[j] = v[j+1];

v[j+1] = tmp;

przest = 1;

}

j=j+1;

}

}

while (n >0 && przest );

printf("Ciag rosnaco posortowany\n");

i=0; while(i < n0) { printf("%3d", v[i]); i=i+1; } printf("\n");

system("pause");

return 0;

}

TEST

i=0 1 2 3 4 5 6 7

8 3 5 7 1 4 10 9

3 8 5 7 1 4 10 9 j = 0

3 5 8 7 1 4 10 9 j = 1

3 5 7 8 1 4 10 9 j = 2

3 5 7 1 8 4 10 9 j = 3

3 5 7 1 4 8 10 9 j = 4

3 5 7 1 4 8 10 9 j = 5

3 5 7 1 4 8 9 10 j = 6

i = 0

3 5 7 1 4 8 9 10 j = 0

3 5 7 1 4 8 9 10 j = 1

3 5 1 7 4 8 9 10 j = 2

3 5 1 4 7 8 9 10 j = 3

3 5 1 4 7 8 9 10 j = 4

3 5 1 4 7 8 9 10 j = 5

i = 1

3 5 1 4 7 8 9 10 j = 0

3 1 5 4 7 8 9 10 j = 1

3 1 4 5 7 8 9 10 j = 2

3 1 4 5 7 8 9 10 j = 3

3 1 4 5 7 8 9 10 j = 4

i = 2

1 3 4 5 7 8 9 10 j = 0

1 3 4 5 7 8 9 10 j = 1

1 3 4 5 7 8 9 10 j = 2

1 3 4 5 7 8 9 10 j = 3

i = 3

1 3 4 5 7 8 9 10 j = 0

1 3 4 5 7 8 9 10 j = 1

1 3 4 5 7 8 9 10 j = 2

i = 4

Ciag rosnaco posortowany

1 3 4 5 7 8 9 10

*/

6. Marsz

gnuplot excel

6a) Dana jest pozycja początkowa obiektu w pkt P₀ =A(0,0).

Algorytm oblicza kolejne pozycje dla k = 1,2, ... n = 20 symulu­­jąc ruch w kierunku celu B(20, 20). Pozycje P_k są kolejno losowane przez funkcję rand (0 ≤ rand < 1) i odchylane od zadanego kierunku wzdłuż linii przekątnej maksymalnie o daną odległość r (gdy r=0 to punkty są na prostej w odległościach d0=√2 od siebie)

Oblicz odległość między uzyskanym punktem a pkt docelowym B

Wyniki zapisane w pliku może wykreślić program gnuplot

r = 0 r = 1

6b) Dana jest pozycja początkowa P₀ =A(0,0) w chwili t₀ = 0 obiektu posiadającego masę m. Algorytm oblicza kolejne pozycje dla t = t₁, t₂ ... t_n symulu­­jąc ruch w kierunku celu B(20, 20). Pozycje są obliczane przez rozwiązanie równania ruchu pod wpływem losowej siły

Program Marsz;

var

fout1: Text; i,n:integer;

d,y,r,r0,alf:real; ax,bx,ay,by:real;

BEGIN

Assign(fout1, 'plo1.dat'); ReWrite(fout1);

randomize;

bx:=20; by:=20; n:=20; r:=1.0; // 0, 2, 4

ax:=0; ay:=0; r0:=bx/n; x:=ax; y:=ay;

writeln(fout1,x:10:4,y:10:4);

for i:=1 to n do begin

alf :=2*pi*random(100)/100;

x:=x+d0+r*sin(alf);// x:=x+d0+2*r*(random(100)/100.0-0.5);

y:=y+d0+r*cos(alf);// y:=y+d0+2*r*(random(100)/100.0-0.5);

writeln(fout1, x:10:4, y:10:4);

end;

d:=sqrt((x-bx)*(x-bx)+(y-by)*(y-by));

writeln(fout1); close(fout1);

writeln(d:10:4);

END.

plo1_4.dat

http://www.bloodshed.net/devpascal.html

7 Sortowanie przez wstawianie

// Posortować tablicę n elementów w porządku rosnącym

// za pomocą metody sortowania poprzez wstawianie

0 1 2 3 4 5 6 7

8, 3, 5, 7, 1, 16, 10, 9 i = 1 tmp = 3

i=1 przes vj= 8 na j= 1

i =... 2, 3 ....

0 1 2 3 4 5 6 7

3 5 7 8 1 16 10 9 i = 4 tmp = 1

i=4 przes vj= 8 na j= 4

i=4 przes vj= 7 na j= 3

i=4 przes vj= 5 na j= 2

i=4 przes vj= 3 na j= 1

i = ... 5,6

0 1 2 3 4 5 6 7

1 3 5 7 8 10 16 9 i = 7 tmp = 9

i=7 przes vj=16 na j= 7

i=7 przes vj=10 na j= 6

1 3 5 7 8 9 10 16 i= 7 j=5 =

//Dla i=1 .. n-1

// wstaw v[i] na odpowiednie miejsce v[0], v[1] ... v[i-1}

// czyli dla j = i-1, j-2 , ... 0

// gdy v[j] > v[j+1] to ten element przesun w prawo

static int v[] = {8,3,5,7,1,16,10,9}; // zloz 11

// static int v[] = {1,3,5,10,8,9,7,16};

// optymistyczny 5 prawie uporzadkowany

// static int v[] = {16,10,9,8,7,5,3,1};

// pesymistyczny 28 odwrotnie uporządk.

int k,tmp,i,j,n=8;

// W każdej iteracji pętli zewn. porównujemy v[i] z elementami juz posortowanej tablicy w celu znalezienia odpowiedniego dla niego miejsca.

for ( i = 1; i < n ; i++) {

tmp = v[i];

for ( j = i-1; j >= 0 && v[j] > tmp; j ─ ─ )

v[j + 1] = v[ j ];

v[j + 1] = tmp;

}

Sortownie przez wstawienie Insert Sort

- ciag niesortowany

8 3 5 7 1 16 10 9

Wynik

i=1 przes vj= 8 na j= 1

3 8 5 7 1 16 10 9 i= 1 j=0

i=2 przes vj= 8 na j= 2

3 5 8 7 1 16 10 9 i= 2 j=1

i=3 przes vj= 8 na j= 3

3 5 7 8 1 16 10 9 i= 3 j=2

i=4 przes vj= 8 na j= 4

i=4 przes vj= 7 na j= 3

i=4 przes vj= 5 na j= 2

i=4 przes vj= 3 na j= 1

1 3 5 7 8 16 10 9 i= 4 j=0

1 3 5 7 8 16 10 9 i= 5 j=5

i=6 przes vj=16 na j= 6

1 3 5 7 8 10 16 9 i= 6 j=5

i=7 przes vj=16 na j= 7

i=7 przes vj=10 na j= 6

1 3 5 7 8 9 10 16 i= 7 j=5

Ciag rosnaco posortowany złoz=10

1 3 5 7 8 9 10 16

Testy warunku j<=0

Sortownie przez wstawienie Insert Sort

-8 -3 -5 -7 -1 -16 -10 -9

v[-1]=0 i,n,j = 5 8 -1

-16 -10 -9 -8 -7 -5 -3 -1

bez kontroli granicy j<=0

-8 -3 -5 -7 -1 -16 -10 -9

v[-1]=0 i,n,j = 5 8 -1

v[-2]=0 i,n,j = 5 8 -2

BLAD ==========>

niestatyczna

- ciag niesortowany

-8 -3 -5 -7 -1 -16 -10 -9

v[-1]=2009187043 i,n,j = 5 8 -1

v[-2]=-16 i,n,j = 5 8 -2

v[-3]=5 i,n,j = 5 8 -3

v[-4]=-4 i,n,j = 5 8 -4

v[-1]=-16 i,n,j = 6 8 -1

Ciag rosnaco posortowany

-10 -92009187043 -8 -7 -5 -3 -1

j = i ─ 1; // for (j = i ─ 1; j >= 0 && v[j] > tmp; j ─ ─) v[j+1] = v[j];

while (j<0?printf("v[%d]=%d .... \n“, j, v[j], i, n, j )

:0, /* j >= 0 && */ v[j]>=tmp )

v[j + 1] = v[ j ─ ─ ];

v[j+1] = tmp;

// inna wersja

for (i = n-2; i >= 0; i--)

{

j = i;

tmp = v[i];

while ((j < n-1) && (x > v[j+1]))

{

v[j] = v[j+1];

j++;

}

v[j]=tmp;

}

Przyjmuje wskaźnik do tablicy i wymiar tablicy

void inSort(int *t, int n)

{

int i,j; // Do iteracji

int x; // Zmienna pomocnicza

for (i = n-2; i >= 0; i--)

{

j = i;

x = t[i];

while ((j < n-1) && (x > t[j+1]))

{

t[j] = t[j+1];

j++;

}

}

8 Sortowanie przez wybór

// Cel: Posortować tablice n elementów w porządku rosnącym

// używając metody sortowania poprzez wybór

....

static int v[] = {8,3,7,5,1,10,9,16}; // 24

// static int v[] = {1,3,5,7,8,9,10,16}; // 21 uporzadkowany

// static int v[] = {1,3,5,10,8,9,7,16}; //22 prawie uporzadkowany

// static int v[] = {10,9,5,7,8,4,6,1}; // 25 odwrotnie uporzadkowany

.....

/* Petla zewnetrzna jest wykonywana raz dla kolejnego elementu tablicy

dokonujac podzialu na czesc posortowana i nieposortowana.

W kazdej iteracji w tej petli dwa elementy mogą byc zamienione

Petla wewnetrzna znajduje pozycje najmniejszego elementu na czesci

nieposortowanej i zamieniamy wartość z tej pozycją

z wartości pozycji a na koncu posortowanej częsci */

for ( i = 0; i < n-1; i++)

{

// Dla każdej iteracji, zaczynamy z elementem jako tym

// o indeksie. imin i szukamy indeksu o elemencie najmniejszym

imin = i;

for ( j=i+1; j < n; j++)

if (v[j] < v[imin]) // szukamy najmniejszego elementu

imin = j;

if (i!=imin) { // ?? CZY TEN WARUNEK, CZY PODNIESIE EFEKTYWNOŚĆ ??

tmp = v[i]; //najmniejszy element zostanie znaleziony

v[i] = v[imin]; //zamieniamy go z dotychczasowym minimum.

v[imin] = tmp;

// for(k = 0; k < n; k++ ) printf("%3d", v[k]); printf("\n\t\t\ti=%3d imin = %d\n", i,imin);

}

}

printf("Ciag rosnaco posortowany zloz= %d\n" ,z);

for (i=0;i < n;i++) printf("%3d", v[i]); printf("\n");

return 0;

}

/*

Sortownie przez wybor Select Sort - ciag niesortowany

8 3 5 7 1 4 10 9

Ciag rosnaco posortowany

1 3 4 5 7 8 9 10

TEST

i=0 1 2 3 4 5 6 7

8 3 5 7 1 4 10 9

1 3 5 7 8 4 10 9

i= 0 imin = 4

i= 1 imin = 1

1 3 4 7 8 5 10 9

i= 2 imin = 5

1 3 4 5 8 7 10 9

i= 3 imin = 5

1 3 4 5 7 8 10 9

i= 4 imin = 5

i= 5 imin = 5

1 3 4 5 7 8 9 10

i= 6 imin = 7

Ciag rosnaco posortowany

1 3 4 5 7 8 9 10

Naciśnij dowolny klawisz, aby kontynuować . . .

*/

9 Symulacja układu dynamicznego

int main()

{

double t,dt = 0.025, dydt,y=0;

int i;

fw1 = fopen("plosym1.dat","w");

fw2 = fopen("plosym2.dat","w");

for (t=0; t<=5; t=t+dt)

{

dydt = 1-y; // model

printf("%8.2lf%8.2lf%8.2lf\n",t,dydt,y);

fprintf(fw1,"%8.2lf%8.2lf%8.2lf\n",t,dydt);

fprintf(fw2,"%8.2lf%8.2lf%8.2lf\n",t,y);

y = y + dt * dydt; //metoda całkowania

}

}

int main()

{ static double dydt[10],y[] = {0};

double t,dt = 0.025, tmax=5; dydt,y[0]=0;

int i, n=1;

fw1 = fopen("plosym1.dat","w");

fw2 = fopen("plosym2.dat","w");

for (t=0; t < tmax+dt/2; t=t+dt)

{

dydt[0] = 1-y[0]; // model

printf("%8.2lf%8.2lf%8.2lf\n",t,dydt[0],y[0]); // wyjscie

fprintf(fw1,"%8.2lf%8.2lf%8.2lf\n",t,dydt[0]);

fprintf(fw2,"%8.2lf%8.2lf%8.2lf\n",t,y[0]);

for (i=0; i< n; i++ ) // metoda całkowania

y[i] = y[i] + dt * dydt[i];

}

}

10 Rekurencja

//10a,b Rekurencja - drukowanie cyfr

#include<stdio.h>

#include<stdlib.h>

void wypr_iter(int n);

void wypr_rek1(int n);

void wypr_rek2(int n);

void wypr_rek3(int, char*);

int p=10;

int main()

{

int d;

char a[20];

printf("Wpisz liczbe calkowita: ");

scanf("%d",&d);

itoa(d,a,p);

printf("\nWynik z bibl itoa(n,a)= %s \n",a);

printf("\nIteracyjnie ");

wypr_iter(d);

printf("\n Rekur1(n) z i=n/10 = ");

wypr_rek1(d);

printf("\n Rekur2(n) = ");

wypr_rek2(d);

printf("\n");

printf("\n Rekur3(n.a) z tekstem ");

printf("Adres a =%u\n ",a);

wypr_rek3(d,a);

printf("%Wynik %s \n",a);

printf("\n");

system("pause");

}

void wypr_iter(int n)

{

char d[10];

int i;

i=0;

do

{

d[i]= n%p+'0';

i++;

}while((n=n/p) > 0);

while(--i >= 0)

printf("%c",d[i]);

printf("\n");

}

void wypr_rek1(int n)

{

int i=n/p; // printf("{%d} ",i);

if(i!=0) wypr_rek1(i);

printf("%c",n%p+'0');

}

void wypr_rek2(int n)

{

int i;

if(i=n/p) wypr_rek2(i);

printf("%c",n%p+'0');

}

void wypr_rek3(int n, char *a)

{

int i; // printf("%u ",a);

if(i=n/p) wypr_rek3(i,a); // printf("powrot z i = %d\n",i);

// printf("%u ",a);

*--a=n%p+'0'; *a=0;

}

/*

Wpisz liczbe calkowita: 1234

1234

Rekur

{123} {12} {1} {0} 1234

Naciśnij dowolny klawisz, aby kontynuować . . .

*/

10c Rekurencja Symbol Newtona

 n 

 k 

obliczanie (n po k) 4 po 2 = 6

n k

--------

4 2

+ 3 1

+ + 2 0

- - - a= 1

+ + 2 1

+ + + 1 0

- - - - a= 1

+ + + 1 1

-- -- -- -- b= 1 c= 2

-- -- -- b= 2 c= 3

- - a= 3

+ 3 2

+ + 2 1

+ + + 1 0

- - - - a= 1

+ + + 1 1

-- -- -- -- b= 1 c= 2

- - - a= 2

+ + 2 2

-- -- -- b= 1 c= 3

-- -- b= 3 c= 6

rekurencja (n po k)=( 4 po 2) = 6

int newton_rec(int n, int k) {

if ( n==k || k==0 )

return 1;

else

return newton_rec(n-1, k-1) + newton_rec(n-1, k);

}

Metoda Iteracyjna

7 po 3

1 7

2 21

3 35

7 po 4

1 7

2 21

3 35

4 35

int wsp_newton_iter(int n, int k)

{

int w,i;

w = 1;

for (i = 1; i<= k; i++ )

w = w * ( n - i + 1 ) / i;

return w;

}

Obliczanie (n po k)

Podaj k i d: iteracja (n po k)=( 6 po 2) = 15

n k

-------

6 2

+ 5 1

+ + 4 0

- - - a= 1

+ + 4 1

+ + + 3 0

- - - - a= 1

+ + + 3 1

+ + + + 2 0

- - - - - a= 1

+ + + + 2 1

+ + + + + 1 0

- - - - - - a= 1

+ + + + + 1 1

-- -- -- -- -- -- b= 1 c= 2

-- -- -- -- -- b= 2 c= 3

-- -- -- -- b= 3 c= 4

-- -- -- b= 4 c= 5

- - a= 5

+ 5 2

+ + 4 1

+ + + 3 0

- - - - a= 1

+ + + 3 1

+ + + + 2 0

- - - - - a= 1

+ + + + 2 1

+ + + + + 1 0

- - - - - - a= 1

+ + + + + 1 1

-- -- -- -- -- -- b= 1 c= 2

-- -- -- -- -- b= 2 c= 3

-- -- -- -- b= 3 c= 4

- - - a= 4

+ + 4 2

+ + + 3 1

+ + + + 2 0

- - - - - a= 1

+ + + + 2 1

+ + + + + 1 0

- - - - - - a= 1

+ + + + + 1 1

-- -- -- -- -- -- b= 1 c= 2

-- -- -- -- -- b= 2 c= 3

- - - - a= 3

+ + + 3 2

+ + + + 2 1

+ + + + + 1 0

- - - - - - a= 1

+ + + + + 1 1

-- -- -- -- -- -- b= 1 c= 2

- - - - - a= 2

+ + + + 2 2

-- -- -- -- -- b= 1 c= 3

-- -- -- -- b= 3 c= 6

-- -- -- b= 6 c=10

-- -- b=10 c=15

ekurencja (n po k)=( 6 po 2) = 15

11. Równania rekurencyjne

Dana zależnośc rekurencyjna

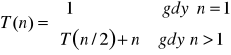
1. obliczyć „ręcznie” dla n = 16

2. wyprowadzić ogólną postać jawną T(n)

3. określić algorytm iteracyjny (przetestować „ręcznie”)

#include<stdio.h>

#include<math.h>

#define UL unsigned long int

#define A 3

/*------------------------------------------*/

UL row1r(UL n) {

if( n==1 ) return 1;

else return row1r(n/2)+n;

};

/*------------------------------------------*/

UL row1i(UL n) {

UL s = 0;

do

s = s + n;

while ((n/=2)>0);

return s;

};/*------------------------------------------*/

UL row1ii(UL n) {

UL s = 0,a=1;

do {

s = s + a;

a = 2*a;

} while ((n/=2)>0);

return s;

};

/*---------------*/

int main()

{

UL n = 16; // 1;

printf("n = %d \n", n);

printf("i1=%d,ii1=%d,r1=%d,s1=%d\n",

row1i(n), row1ii(n), row1r(n), 2*n-1);

}

// Rekurencja - rownania - Test Windows (DEV-CPP)

#include<stdio.h>

//#include<stdlib.h>

//#include<time.h>

#include<math.h>

#define UL unsigned long int

#define A 3

UL row1r(UL n) {

if( n==1 ) return 1;

else return row1r(n/2)+n;

};

UL row1i(UL n) {

UL s = 0;

do

s = s + n;

while ((n/=2)>0);

return s;

};

UL row1it(UL n) {

UL s = 0,a=1;

do {

s = s + a;

a = 2*a;

} while ((n/=2)>0);

return s;

};

/*---------------------------------------------------*/

UL row2ar(UL n) {

UL t;

if( n==0 ) t = 0;

else t = 3*row2ar(n-1)-2;

printf("%4d %4d\n",n,t);

return t;

};

UL row2br(UL n) {

UL t;

if( n==0 ) t = 2;

else t = 2*row2br(n-1)+4;

printf("%4d %4d\n",n,t);

return t;

};

UL row2ai(UL n) {

UL s = 0,i=0;

while ((i++)<n){

s = 3*s -2;

printf("%4d %4d",i,s); }

printf("------------\n");

return s;

};

UL row2bi(UL n) {

UL s = 2,i=0;

while ((i++)<n){

s = 2*s + 4;

printf("%4d %4d",i,s); }

printf("------------\n");

return s;

};

UL row3r(UL n) {

UL x;

if( n==1 ) x=1;

else x = A*row3r(n/2)+n;

printf("%4d",n);

return x;

};

UL row3i(UL n) {

UL s = 0,i=1;

do {

s = A*s + i; printf("%4d",i); }

while ((i*=2)<=n);

printf("-po 3i -> -----------\n");

return s;

};

UL row3it(UL n) {

UL s=0,i=1;

do {

s = s + n*i;

i=A*i; printf("%4d",n);

} while (n/=2);

printf("-po 3it <- -----------\n");

return s;

};

int main()

{

int i,j;

UL n,s,x,k;

n = 16;

printf("-----------------\n n = %d \n", n);

printf("i1=%d,i1t=%d,r1=%d,s1=%d\n", row1i(n),row1it(n), row1r(n),2*n-1);

printf("\nr2=%d\n", row3r(n));

printf("i3=%d,i3t=%d,s3LJ=%d s3JR=%d\n", row3i(n), row3it(n),

s=3*pow(n,log(3.0)/log(2.0)) - 2*n, // ); //LJ

s=3*pow(3,(log(n)/log(2))) -2*n); //JR

n=4;

printf("-----------------\n n = %d \n", n);

printf("\np2ar=%d,p2ai=%d,s2a=%d \n", row2ar(n), row2ai(n),

s=1-pow(A,(double)n));

printf("\np2br=%d,p2bi=%d,s2b=%d \n", row2br(n), row2bi(n),

s=6*pow (2.0,(double)n ) -4.0 );

printf("\nk = %6.4lf \n",log(2.0)/log(n));

system("pause");

}

/*

-----------------

n = 16

i1=31,i1t=31,r1=31,s1=31

1 2 4 8 16

r2=211

16 8 4 2 1-po 3it <- -----------

1 2 4 8 16-po 3i -> -----------

i3=211,i3t=211,s3LJ=211 s3JR=211

-----------------

n = 4

1 -2 2 -8 3 -26 4 -80------------

0 0

1 -2

2 -8

3 -26

4 -80

p2ar=-80,p2ai=-80,s2a=-80

1 8 2 20 3 44 4 92------------

0 2

1 8

2 20

3 44

4 92

p2br=92,p2bi=92,s2b=92

k = 0.5000

Aby kontynuować, naciśnij dowolny klawisz . . .

*//

11. QuickSort

// Program: sortowanie szybkie

// Cel: Posortować n elementową tablicę w porządku rosnącym

// używając metody sortowania szybkiego

#include <stdio.h>

#include <string.h>

#include <stdlib.h>

#include <iostream.h>

class sort {

private:

int *X; //Lista elementów danych

int n; //Liczba elementów na liście

public:

sort (int size) { X = new int[n=size]; }

~sort( ) { delete [ ]X; }

void load_list (int input[ ] );

void show_list (char *title);

void quick_sort( int first, int last);

};

void sort::load_list(int input[ ])

{

for (int i = 0; i < n; i++)

X[i] = input[i];

}

void sort::show_list( char *title)

{

cout << "\n" << title;

for (int i = 0; i < n; i++)

cout << " " << X[i];

cout << "\n";

}

void sort::quick_sort( int first, int last)

{

//zmienna "temp" jest tymczasową przestrzenią używaną podczas zamiany

int temp;

if (first < last)

{

//Zaczynamy z osią jako pierwszym elementem listy

int pivot = X[first];

//Zmienna "i" jest używana do przeszukiwania z lewej strony.

int i = first;

//Zmienna "j" jest używana do przeszukiwania z prawej strony.

int j = last;

while (i < j)

{

// Przeszukujemy listę w poszukiwaniu elementu, który jest większy // lub równy // wybranej osi. Szukamy od lewej strony.

while (X[i] <= pivot && i < last)

i += 1;

// Przeszukujemy listę w poszukiwaniu elementu, który jest mniejszy // lub równy // wybranej osi. Szukamy od prawej strony.

while (X[j] >= pivot && j > first)

j -= 1;

if (i < j) //zamień(X[i],X[j])

{

temp = X[i];

X[i] = X[j];

X[j] = temp;

}

}

//zamień(X[j],X[first])

temp = X[first];

X[first] = X[j];

X[j] = temp;

//Wykonujemy rekursywne szybkie sortowanie na dwóch połówkach

quick_sort(first, j-1);

quick_sort(j+1, last);

}

}

// Testuje szybkie sortowanie

int main(void)

{

sort sort_obj (5);

static int unsorted_list[] = {54, 6, 26, 73, 1};

sort_obj.load_list(unsorted_list);

sort_obj.show_list("Lista ");

sort_obj.quick_sort(0,4);

sort_obj.show_list("Lista posortowana ");

system("pause");

}

/* Sortowanie szybkie */

#include <stdio.h>

#define TS 100

int tab[TS];

int PrintTab( int tab[], int size )

{

int i, tCount = 0;

for ( i=0; i<size; i++ )

{

printf( "%d, ", tab[i] );

if ( tCount++ > 8 )

{

tCount = 0;

printf("\n");

}

}

}

void swap( int v[], int i, int j )

{

int p;

p = v[i];

v[i] = v[j];

v[j] = p;

}

void QuickSort( int v[], int left, int right )

{

int i, last;

if ( left >= right ) return;

swap( v, left, (left+right)/2 );

last = left;

for (i=left+1; i<=right; i++)

if ( v[i] < v[left] )

swap(v, ++last, i );

swap( v, left, last );

QuickSort( v, left, last-1 );

QuickSort( v, last+1, right );

}

int main()

{

int i;

for ( i=0; i<TS; i++ )

tab[i] = rand() % 255;

printf( "\n\nprzed sortowaniem:\n" );

PrintTab( tab, TS );

QuickSort( tab, 0, TS-1 );

printf( "\n\npo sortowaniu:\n" );

PrintTab( tab, TS );

system("pause");

return 0;

}

Listy

1xx

( Przetwarzanie tekstów - podstawy ) -

podstawy.doc

      Wyszukiwanie wzorca algorytmem KMP

Do zrozumienia tego rozdziału niezbędne jest zapoznanie się z rozdziałami:

OL001-Pojęciapodstawowe przy przetwarzaniu tekstów

OL002 - Wyszukiwanie maksymalnego prefikso-sufiksu

OL004 - Wyszukiwanie wzorca algorytmem MP

Profesor Donald Knuth przeanalizował dokładnie algorytm Morrisa-Pratta i zauważył, iż można go jeszcze ulepszyć. Ulepszenie to polega na nieco innym sposobie wyznaczania tablicy Π[ ] w stosunku do algorytmu MP. Otóż oryginalnie tablica ta zawiera maksymalne szerokości prefikso-sufiksów kolejnych prefiksów wzorca. Załóżmy, iż w trakcie porównania dochodzi do niezgodności na pozycji znaku A w łańcuchu przeszukiwanym ze znakiem B we wzorcu (A, B i C oznaczają nie konkretne literki, ale różne znaki łańcucha i wzorca) :

łańcuch s1	b			b	A	łańcuch s1
	pre- fiks			su- fiks	≠
przed przesunięciem	b	C		b	B	wzorzec s2
					≠
	po przesunięciu			b	C	wzorzec s2

W celu uniknięcia po przesunięciu okna wzorca natychmiastowej niezgodności musimy dodatkowo zażądać, aby znak C leżący tuż za prefikso-sufiksem prefiksu we wzorcu był różny od znaku B, który poprzednio wywołał niezgodność. Algorytm MP nie sprawdzał tej cechy.

Tablicę szerokości prefikso-sufiksów uwzględniającą tę cechę będziemy nazywali tablicą Next[ ]. Kolejne jej elementy są maksymalnymi szerokościami prefikso-sufiksów prefiksu wzorca. Jeśli dany prefikso-sufiks nie istnieje (nawet prefikso-sufiks pusty), to element tablicy ma wartość -1 (w poprzedniej wersji algorytmu wartownik występował tylko w elemencie o indeksie 0).

NP Wyznaczymy tablicę Next[ ] dla wzorca ABACABAB - identyczny wzorzec jak w rozdziale o tworzeniu tablicy Π[ ].

Lp.	Tworzona tablica Next[ ]	Opis
1.	s: A B A C A B A B  Next:-1 i: 0 1 2 3 4 5 6 7 8	Element Next[0] jest zawsze równy -1. Pełni on rolę wartownika, dzięki któremu upraszcza się algorytm wyznaczania kolejnych elementów tablicy.
2.	s: A B A C A B A B Next:-1 0 i: 0 1 2 3 4 5 6 7 8	Prefiks jednoznakowy A posiada zawsze prefikso-sufiks pusty. Dodatkowo znak A leżący tuż za prefikso-sufiksem oraz znak B leżący za prefiksem są różne. Zatem istnieje prefikso-sufiks pusty o szerokości 0 i to wpisujemy do tablicy.
3.	s: A B A C A B A B Next:-1 0-1 i: 0 1 2 3 4 5 6 7 8	Prefikso-sufiks prefiksu dwuznakowego AB ma szerokość 0. Jednakże znak A leżący tuż za prefikso-sufiksem pustym oraz znak A leżący tuż za prefiksem jest tym samym znakiem. Skoro tak, to prefikso-sufiks nie istnieje - wpisujemy -1.
4.	s: A B A C A B A B Next:-1 0-1 1 i: 0 1 2 3 4 5 6 7 8	Prefikso-sufiks prefiksu ABA ma szerokość 1 (obejmuje pierwszą i ostatnią literkę A). Znak B leżący tuż za prefikso-sufiksem oraz znak C leżący za prefiksem są różne. Zatem do tablicy wprowadzamy 1.
5.	s: A B A C A B A B Next:-1 0-1 1-1 i: 0 1 2 3 4 5 6 7 8	Prefiks ABAC ma prefikso-sufiks pusty o szerokości 0. Jednakże za prefikso-sufiksem i za prefiksem występuje ten sam znak. Zatem w tablicy umieszczamy -1.
6.	s: A B A C A B A B Next:-1 0-1 1-1 0 i: 0 1 2 3 4 5 6 7 8	Prefiks ABACA posiada prefikso-sufiks o szerokości 1 (pierwsza i ostatnia litera A). Jednakże za prefikso-sufiksem i prefiksem występuje ten sam znak B. Z tablicy odczytujemy zatem szerokość następnego prefikso-sufiksu - Next[1] = 0. Jest to prefikso-sufiks pusty. W tym przypadku za prefikso-sufiksem wystąpi litera A, która różni się od litery B za prefiksem. Jest to zatem poszukiwany prefikso-sufiks i szerokość 0 wpisujemy do tablicy.
7.	s: A B A C A B A B Next:-1 0-1 1-1 0-1  i: 0 1 2 3 4 5 6 7 8	Prefiks ABACBA posiada prefikso-sufiks o szerokości 2 (AB z przodu i z tyłu). Jednakże za prefikso-sufiksem i za prefiksem występuje ten sam znak A. Odczytujemy z tablicy szerokość następnego prefikso-sufiksu Next[2] = -1. Prefikso-sufiks taki nie istnieje, zatem w tablicy umieszczamy -1.
8.	s: A B A C A B A B Next:-1 0-1 1-1 0-1 3  i: 0 1 2 3 4 5 6 7 8	Prefiks ABACABA posiada prefikso-sufiks o szerokości 3 (ABA). Znak C za prefikso-sufiksem jest różny od znaku B za prefiksem, zatem w tablicy umieszczamy 3.
9.	s: A B A C A B A B  Next:-1 0-1 1-1 0-1 3 2 i: 0 1 2 3 4 5 6 7 8	Cały wzorzec ABACABAB posiada prefikso-sufiks o szerokości 2 (AB). Ponieważ nie ma już możliwości sprawdzenia znaku A leżącego tuż za prefikso-sufiksem ze znakiem leżącym za wzorcem, to w tablicy umieszczamy 2. Tablica Next[ ] jest gotowa.

Porównajmy tablicę  Π[ ] z tablicą Next[ ]:

wzorzec		A	B	A	C	A	B	A	B
tablica Π[ ]	-1	0	0	1	0	1	2	3	2
tablica Next[ ]	-1	0	-1	1	-1	0	-1	3	2
indeks	0	1	2	3	4	5	6	7	8

Algorytm wyszukiwania wzorca wykorzystujący tablicę Next[ ] jest identyczny z algorytmem wykorzystującym tablicę Π[ ], zatem nie będziemy go tutaj opisywać. Tablica Next[ ] pozwala bardziej efektywnie wyszukiwać wystąpienia wzorców, ponieważ pomijane są puste przebiegi. Klasa złożoności obliczeniowej jest równa O(m + n), gdzie m jest ilością znaków wzorca, a n jest ilością znaków tekstu.

Dane wejściowe

s -

łańcuch wzorca, dla którego mamy wyznaczyć zawartość tablicy Next[ ]. Dla poprawności działania algorytmu bardzo istotne jest, aby na końcu łańcucha był wstawiony wartownik - znak o kodzie innym niż kody znaków wzorca. W języku C++ będzie to zagwarantowane, ponieważ łańcuchy znakowe kończą się znakiem o kodzie 0

Dane wyjściowe

Next[ ] -

tablica zawierająca szerokości prefikso-sufiksów kolejnych prefiksów wzorca s. Indeksy  rozpoczynają się od wartości 0 (pusty prefiks) do wartości |s| (prefiks niewłaściwy).

Zmienne pomocnicze

i	- zmienna indeksująca kolejne komórki tablicy Next[ ]
b	- wyliczana szerokość prefikso-sufiksu

Lista kroków

K01: Next[0] ← -1;   b ← -1	Strażnika -1 umieszczamy w pierwszym elemencie tablicy Next[ ] oraz w b
K02: Dla i = 1, 2, ..., |s|: wykonuj kroki K03 ... K05	Pętla K02 wyznacza indeksy kolejnych elementów tablicy Next[ ].
K03:     Dopóki (b > -1) (s[b] ≠ s[i - 1]): wykonuj b ← Next[b]	W pętli K03 szukamy prefikso-sufiksu b prefiksu wzorca, który da się rozszerzyć. Z pętli wychodzimy, jeśli natrafimy na wartownika lub prefikso-sufiks jest rozszerzalny
K04:     b ← b + 1	Rozszerzamy prefikso-sufiks
K05:     Jeśli s[i] = s[b], to Next[i] ← Next[b] inaczej Next[i] ← b	Jeśli następny znak wzorca jest taki sam jak znak tuż za prefikso-sufiksem, to prefikso-sufiks redukujemy. Wynik zapisujemy na kolejnej pozycji w tablicy Next[ ].
K06: Zakończ algorytm

Program

W przykładowym programie korzystamy z tablic znakowych do przechowywania łańcucha c₁ i poszukiwanego w nim wzorca c₂.

//P005 (C)2007 J.W I-LO Tarnów #include <iostream> using namespace std; const int N = 70; // długość łańcucha c1 const int M = 3; // długość łańcucha c2 - wzorzec main() { char c1[N+1], c2[M+1]; int i,b,p,Next[M+1]; srand((unsigned)time(NULL)); // Generujemy łańcuch do przeszukania for(i = 0; i < N; i++) c1[i] = 65 + rand() % 4; c1[N] = '\0'; // Generujemy wzorzec for(i = 0; i < M; i++) c2[i] = 65 + rand() % 4; c2[M] = '\0'; // Wyświetlamy dane wejściowe: cout << "s2 = " << c2 << "\n\ns1 = " << c1 << "\n "; // Obliczamy tablicę Next[] Next[0] = b = -1; for(i = 1; i <= M; i++) { while((b > -1) && (c2[b] != c2[i - 1])) b = Next[b]; b++; Next[i] = (c2[i] == c2[b]) ? Next[b] : b; } // Szukamy pozycji wzorca algorytmem KMP b = 0; p = -1; for(i = 0; i <= N - 1; i++) { while((b > -1) && (c2[b] != c1[i])) b = Next[b]; if(++b < M) continue; p = i - b + 1; break; } // Jeśli znaleziono wzorzec w łańcuchu, wyświetlamy go if(p >= 0) { for(i = 0; i < p; i++) cout << " "; cout << c2; } else cout << "Wzorzec nie znaleziony."; cout << endl << endl; system("pause"); }

s2 = DBA s1 = DACCDCBCADCCACCAACDADCDBAACABDCCBDDADBCABDACDBDCDBBABABDDBCCDBBBAADABD DBA

      

Wyszukiwanie wzorca algorytmem MP

Na początek podamy uproszczony algorytm wyszukiwania wzorca, zwany algorytmem MP (Morrisa-Pratta). W algorytmie wykorzystuje się tablicę Π[ ], której tworzenie opisane jest w rozdziale o wyszukiwaniu maksymalnego prefikso-sufiksu. Korzysta się z następującej własności tekstów:

Załóżmy, iż poszukujemy pierwszego wystąpienie wzorca s₂ w danym łańcuchu tekstowym s₁. W trakcie porównywania kolejnych znaków łańcucha ze znakami wzorca natrafiliśmy na sytuację, w której pewien prefiks wzorca, o długości b znaków, pasuje do prefiksu okna wzorca w łańcuchu s₁ przed pozycją i-tą, jednakże znak s₁[i] różni się od znaku s₂[b], który znajduje się we wzorcu tuż za pasującym prefiksem (na rysunku oznaczono te znaki czerwonym polem z literką X):

		okno wzorca	s[i]
tekst s1		pasujący prefiks okna wzorca	X
		=	≠
wzorzec s2		pasujący prefiks wzorca	X
		b znaków	s[b]

Algorytm N w takiej sytuacji przesuwa okno wzorca o jedną pozycję w prawo względem przeszukiwanego tekstu i rozpoczyna od początku porównywanie znaków wzorca ze znakami okna i nie korzysta zupełnie z faktu zgodności części znaków. To marnotrawstwo prowadzi to do klasy złożoności obliczeniowej O(n²). Tymczasem okazuje się, iż wykorzystując fakt istnienia pasującego prefiksu, możemy pominąć pewne porównania znaków bez żadnej straty dla wyniku poszukiwań. Otóż po stwierdzeniu niezgodności okno wzorca przesuwamy tak, aby przed znakiem s₁[i] znalazł się maksymalny prefikso-sufiks pasującego prefiksu wzorca:

okno wzorca

s[i]

tekst s1

pasujący prefiks okna

X

wzorzec s2

pasujący prefiks wzorca

X

b'

b'

s[b]

wzorzec s2

b' = Π[b]

b'

?

s[b']

Dzięki temu podejściu pomijamy niepotrzebne porównania znaków oraz unikamy cofania się indeksu i (przesuwa się jedynie okno wzorca).

Dla każdego prefiksu wzorca szerokość maksymalnego prefikso-sufiksu można wyznaczyć przed rozpoczęciem wyszukiwania - do tego właśnie celu generujemy tablicę Π[ ]. Dla danej długości prefiksu b możemy z tej tablicy odczytać szerokość maksymalnego prefikso-sufiksu tego prefiksu. W naszym przypadku będzie to:

b' = Π[b]

Teraz porównujemy znak wzorca s₂[b'] (leżący tuż za odczytanym z tablicy prefikso-sufiksem) ze znakiem s₁[i]. Jeśli wciąż mamy niezgodność, to procedurę powtarzamy, aż do wyczerpania się prefikso-sufiksów - w takim przypadku okno wzorca oraz i przesuwamy o jedną pozycję w prawo.

Jeśli otrzymamy zgodność, to pasujący prefiks zwiększa swoją długość o 1 znak. Przesuwamy również pozycję i-tą o 1, ponieważ znak na tej pozycji został już całkowicie wykorzystany przez algorytm MP.

Jeśli prefiks obejmie cały wzorzec (b = |s₂|), to znaleziona zostanie pozycja wzorca w s₁ i będzie ona równa i - b + 1. W przeciwnym razie poszukiwania kontynuujemy w pętli.

Dane wejściowe

s₁ - łańcuch znakowy do przeszukania
s₂ - wzorzec, którego poszukujemy w s₁

Dane wyjściowe

p - pozycja wzorca s₂ w łańcuchu s₁ lub -1, jeśli wzorzec s₂ nie został znaleziony w s₁.

Dane pomocnicze

i - pozycja porównywanego znaku w łańcuchu tekstowym s₁, 0 ≤ i ≤ |s₁|
b - długość prefiksu wzorca s₂ pasującego do prefiksu okna wzorca w łańcuchu s₁. 0 ≤ b ≤ |s₂|.
Π[ ] - tablica o indeksach od 0 do |s₂|, przechowująca szerokości maksymalnych prefikso-sufiksów kolejnych prefiksów wzorca s₂

Lista kroków

K01: Generuj dla wzorca s2 tablicę Π[ ]	Przed rozpoczęciem wyszukiwania wzorca s2 w s1 wyznaczamy dla s2 tablicę szerokości maksymalnych prefikso-sufiksów kolejnych prefiksów.
K02: b ← 0;   p ← -1	Szerokość prefikso-sufiksu ustawiamy na 0, a znalezioną pozycję wzorca w s1 na -1
K03: Dla i = 0, 1, ... ,|s1| - 1: wykonuj kroki K04 ... K07	Pętla K03 wyznacza kolejne znaki w s1, które będą porównywane ze znakami wzorca s2
K04:     Dopóki (b > -1) i s2[b] ≠ s1[i] : b ← Π[b]	Szukamy we wzorcu s2 rozszerzalnego prefiksu pasującego do prefiksu okna wzorca. Pętlę K04 przerywamy, jeśli znajdziemy rozszerzalny prefiks lub napotkamy wartownika -1
K05:     b ← b + 1	Rozszerzamy prefiks o 1 znak. Jeśli prefiks był wartownikiem, to otrzymuje wartość 0.
K06:     Jeśli b < |s2|, to kontynuuj pętlę K03	Jeśli prefiks nie obejmuje całego wzorca, to kontynuujemy pętlę K03, czyli porównujemy znak s2[b] z kolejnym znakiem łańcucha s1.
K07:     p ← i - b + 1 i zakończ	W przeciwnym razie wyznaczamy pozycję okna wzorca w p i kończymy
K08: Zakończ	Tutaj kończymy z p = -1, czyli wzorzec nie został znaleziony.

Program

W przykładowym programie korzystamy z tablic znakowych do przechowywania łańcucha c₁ i poszukiwanego w nim wzorca c₂.

//P004 (C)2007 J.W I-LO Tarnów #include <iostream> using namespace std; const int N = 70; // długość łańcucha c1 const int M = 3; // długość łańcucha c2 - wzorzec main() { char c1[N+1], c2[M+1]; int i,b,p,pi[M+1]; srand((unsigned)time(NULL)); // Generujemy łańcuch do przeszukania for(i = 0; i < N; i++) c1[i] = 65 + rand() % 4; c1[N] = '\0'; // Generujemy wzorzec for(i = 0; i < M; i++) c2[i] = 65 + rand() % 4; c2[M] = '\0'; // Wyświetlamy dane wejściowe: cout << "s2 = " << c2 << "\n\ns1 = " << c1 << "\n "; // Obliczamy tablicę pi[] pi[0] = b = -1; for(i = 0; i < M; i++) { while((b > -1) && (c2[b] != c2[i])) b = pi[b]; pi[i+1] = ++b; } // Szukamy pozycji wzorca algorytmem MP b = 0; p = -1; for(i = 0; i <= N - 1; i++) { while((b > -1) && (c2[b] != c1[i])) b = pi[b]; if(++b < M) continue; p = i - b + 1; break; } // Jeśli znaleziono wzorzec w łańcuchu, wyświetlamy go if(p >= 0) { for(i = 0; i < p; i++) cout << " "; cout << c2; } else cout << "Wzorzec nie znaleziony."; cout << endl << endl; system("pause"); }

s2 = AAC s1 = CCACAABCACCACBABBBDAADADCADBDABCBBADCAADAAACAABCADCDCCBDCCBCADBCBADCAA AAC

Tablica o m elementach zawiera nazwy obiektów

Określ algorytm, który:

a) czyta z pliku wszystkie istniejące pomiędzy obiektami odległosci,

b) wyznacza obiekt, dla którego suma odległości od wszystkich pozostałych obiektów jest najmniejsza.

c) wyznacza i usuwa z tablicy obiekt, którego odległość od elementu wyznaczonego w pkt b) jest największa.

d) drukuje nazwy obiektu wyznaczonego w pkt. b) i usuniętego w pkt. c).

B. Dane są nazwy n elementów zachowane w tablicy jednowymiarowej.

Określ algorytm:

a) czytający z pliku wszystkie istniejące prostoliniowe odległości pomiędzy elementami w sieci połączeń ,

b) wyznaczający element (drukujący jego nazwę), którego suma odległości od wszystkich pozostałych elementów jest najmniejsza.

c) wyznacz i usuń z tablicy element, którego odległość od elementu wyznaczonego w pkt b) jest największa

A

1. Podaj dla jakich wartości początkowych n iteracje są skończone. Określ ich ilość.

a) b) c)

2. Dla danego ogólnego iteracyjnego algorytmu utwórz równoważne

algorytmy, w których występuje pętla

a) z warunkiem na wejściu do pętli ( dopóki, while )

b) z warunkiem na wyjściu z pętli ( powtarzaj, repeat )

Uwaga: instrukcje 1 i 2 nie zmieniają wartości n

ale mogą od niej zależeć.

3. Dana jest zależność p_i+1 = 2 p_i - p_i-1 + 1 i wartości początkowe p_-1 = 1.0, p₀ =0.0.

Podaj algorytm obliczający kolejne wartości p_i dla 0 < i ≤ m

nie używając zmiennych indeksowanych oraz wykonaj obliczenia wartości p_i dla m = 5.

---------------------------------------------------------------------------------------------------------------

B

1. Dla danej zależności r_i+1 = 2 r_j-1 - r_j + 2 i wartości początkowych r₀ = 1.0, r_-1 = 0.0

podaj algorytm obliczający kolejne wartości r_j dla 0 < j ≤ n nie używając

zmiennych indeksowanych oraz wykonaj krokowo obliczenia wartości q_i dla n = 5.

2. Podaj dla jakich wartości początkowych m iteracje są skończone. Określ ich ilość

a) b) c)

3.

Dla danego ogólnego iteracyjnego algorytmu utwórz

równoważne algorytmy, w których występuje pętla

a) z warunkiem na wejściu do pętli ( dopóki, while )

b) z warunkiem na wyjściu z pętli ( powtarzaj, repeat )

Uwaga: instrukcje a i b nie zmieniają wartości m

ale mogą od niej zależeć.

C

1. Dla danego ogólnego iteracyjnego algorytmu utwórz

równoważne algorytmy, w których występuje pętla

a) z warunkiem na wejściu do pętli ( dopóki, while )

b) z warunkiem na wyjściu z pętli ( powtarzaj, repeat )

Uwaga: instrukcje 1 i 2 nie zmieniają wartości k

ale mogą od niej zależeć.

2. Podaj dla jakich wartości początkowych k iteracje są skończone. Określ ich ilość

a) b) c)

3. Dla danej zależności q_j+1 =3+ q_j - 2 q_j-1 i wartości początkowych q₀ = 0.0, q_-1 = 1.0

podaj algorytm obliczający kolejne wartości q_j dla 0 < j ≤ k ( nie należy używać

zmiennych indeksowanych). Wykonaj krokowo obliczenia wartości q_j dla k = 5.

-------------------------------------------------------------------------------------------------------------------------------------------------

D

1. Dla danej zależności s_k+1 = s_k - 2 s_k-1 - 1 i wartości początkowych s₀ = 1.0, s_-1 = 0.0

podaj algorytm obliczający kolejne wartości s_k dla 0 < j ≤ n nie używając

zmiennych indeksowanych oraz wykonując krokowo obliczenia wartości s_k dla n = 5.

2. Dany jest ogólny iteracyjny algorytm. Utwórz równoważne

algorytmy, w których występuje pętla

a) z warunkiem na wejściu do pętli ( dopóki, while )

b) z warunkiem na wyjściu z pętli ( powtarzaj, repeat )

Uwaga: instrukcje A i B nie zmieniają wartości t

ale mogą od niej zależeć.

3. Podaj dla jakich wartości początkowych L iteracje są skończone. Określ ich ilość

a) b) c)

2.Podaj algorytm obliczający szereg

w(z) dla z = z0+i Δz gdzie i = 0,1,2,... n

oraz |Δz| < 10^-6

3. Dla danego ogólnego iteracyjnego algorytmu utwórz równoważne

algorytmy ( schemat lub język), w których występuje pętla z warunkiem

a) na wejściu do pętli - DOPÓKI (warunek) POWTARZAJ instrukcja

b) a wyjściu z pętli - POWTARZAJ instrukcja DOPÓKI (warunek)

4. Dana jest funkcja ff(x), krok Δt i wartości p(-Δt) = 0.0, p(0) =1.0

Podaj efektywny algorytm obliczający następne wartości p(t) dla

0<t<t_mx (nie używaj tablic, zminimalizuj liczbę wywołań funkcji, wykonaj test - wyniki dla uproszczonej funkcji ff(x)=1+x Δt = 1.0

t	-1.0	0.0	1.0	2.0	3.0	4.0	...
p(t)	0.0	1.0	3.0	2.0	3.0	0.4

`

2 . Podaj algorytm obliczający szereg f(t)

dla t = t0+i Δt gdzie i = 0,1,2, ... n

oraz |Δf| < 10^-6

3.Dla danego ogólego iteracyjnego algorytmu utwórz

równoważne algorytmy, w których występuje pętla

a) z warunkiem na wejściu do pętli ( dopóki , while )

b) z warunkiem na wyjści z pętli ( powtarzaj , repeat )

4. Dane są: definicja funkcji fn(t)=1+e^-t/5 sin(t) i

wartości p(t) = 0 w chwili t=0 i t = -Δt

wartości p(t=0) = 0 i p( t = -Δt ) = 0

wartości zmiennej p(t) dla t =0 i p(-Δt) = 0

Podaj algorytm obliczający p(t)

dla 0 < t < t_mx

w n punktach t =-Δt, 2Δt, 3Δt, ... n Δt

w n punktach t = iΔt dla i = 1,2,3...n

gdzie p(t) = p( t-Δt ) - 2 * p(t) + p(t+Δt) / (fn(t) + fn( t-Δt))

------------------------------------------------------------------------------------------------------------------------

void szeregpotegowy()

{

int i,k;

double x,t ,y=1;

t=1.0, x = 2;

k=1;i = 1;

do {

t = -t*x*x*i/(i+3)/k;

y = y + t;

printf ("s%10.4lf %10.4lf %10d\n",y,t,i);

i+=4;k++;

}

while (fabs(t)>1.e-4);

// ASDZadPetle.cpp

#include <math.h>

#include <stdio.h>

#define XX 4

#define YY 4

#define NN 5

//#define NN 0

//#define NN -5

/*ASDZadPetle Daną funkcję PetlaGoTo zastąp równoważnymi funkcjami, w których skok bezwarunkowy będzie zastąpiony 1) pętlą while (warunek) instrukcja 2) pętlą do instrukcja while (warunek) - 2 wersje

Instrukcje wzajemnie od siebie zależą */

void PetlaGoTo() { int i=0, n = NN; double x ,y; x =XX, y = YY;

pocz:

x = x + 1 + y + n + i;

if (n > 0) {

i = i + 1;

y = x + y - 1 - n - 2 * i;

n = n - 1;

goto pocz;

}

printf ("\n\tPetla Go To\t%10d %10d%10.4lf%10.4lf\n",i,n,x,y);

}

void PetlaWhile(){ int i=0, n =NN; double x ,y; x = XX, y = YY;

printf ("\n\tPetla While\t%10d %10d%10.4lf%10.4lf\n",i,n,x,y);

}

void PetlaDoA() { int i=0, n = NN; double x ,y; x = XX, y = YY;

//..........

printf ("\n\tPetla Do vA\t%10d %10d%10.4lf%10.4lf\n",i,n,x,y);

}

void PetlaDoB() { int i=0, n = NN; double x ,y; x = XX, y = YY;

//..........

printf ("\n\tPetla Do vB\t%10d %10d%10.4lf%10.4lf\n",i,n,x,y);

}

int Rmain();

main()

{ printf ("start\n");

PetlaGoTo();

PetlaWhile();

PetlaDoA();

PetlaDoB();

Rmain();

getchar();

}

void RPetlaWhile() { int i=0, n =NN; double x ,y; x = XX, y = YY;

x = x + 1 + y + n + i;

while (n>0){

i = i + 1;

y = x + y - 1 - n - 2 * i;

n = n - 1;

x = x + 1 + y + n + i;

}

printf ("\n\tPetla While\t%10d %10d%10.4lf%10.4lf\n",i,n,x,y);

}

void RPetlaDoA() { int i=0, n = NN; double x ,y; x = XX, y = YY;

x = x + 1 + y + n + i;

do {

//if (n <= 0) break; LUB

if (n > 0)

{

i = i + 1;

y = x + y - 1 - n - 2 * i;

n = n - 1;

x = x + 1 + y + n + i;

}

}while (n>0);

printf ("\n\tPetla Do vA\t%10d %10d%10.4lf%10.4lf\n",i,n,x,y);

}

void RPetlaDoB() { int i=0, n = NN; double x ,y;

x = XX, y = YY;

do {

// if (n <= 0) break; LUB

if (n > 0)

{

x = x + 1 + y + n + i;

i = i + 1;

y = x + y - 1 - n - 2 * i;

n = n - 1;

}

}while (n>0);

x = x + 1 + y + n + i;

printf ("\n\tPetla Do vB\t%10d %10d%10.4lf%10.4lf\n",i,n,x,y);

}

int Rmain()

{

printf ("\n\n\tROZWIAZANE TESTY WYNIKOW\n" );

PetlaGoTo();

RPetlaWhile();

RPetlaDoA();

RPetlaDoB();

return 0;

}

WYNIKI

		A1	B3	C3	D1
i		pi+1 = 2 pi - pi-1 + 1 p-1 = 1.0, p0 =0.0	ri+1 = 2 rj-1 - rj + 2 i r0 = 1.0, r-1 = 0.0	qj+1 =3+ qj - 2 qj-1 q0 = 0.0, q-1 = 1.0	sk+1 = sk - 2 sk-1 - 1 s0 = 1.0, s-1 = 0.0
-1		1	0	1	1
0		0	1	0	0
1		0	1	1	0
2		1	3	4	-1
3		3	1	5	1
4		6	7	0	-4
5		10	-3	-7	8
6		15	19	-4	-21

int i,j,n;

printf("Szkolka n = n - 5\n");

for (i = 2; i<7;i++)

{ n = i*5; printf("i=%4d n=%4d",i,n);

j=0; do {j++; n = n - 5; }

while (!(n == 5)); printf(" j=%4d\n",j);

}

printf("Szkolka m = m + 5\n");

for (i = 0; i>-5;i--)

{ n = i*5; printf("i=%4d n=%4d",i,n);

j=0; do {j++; n = n + 5; }

while (!(n == 5)); printf(" j=%4d\n",j);

}

printf("Szkolka k = k - 10\n");

for (i = 2; i<7;i++)

{ n = i*10; printf("i=%4d n=%4d",i,n);

j=0; do {j++; n = n - 10; }

while (!(n == 10)); printf(" j=%4d\n",j);

}

printf("Szkolka L = L + 5\n");

for (i = 0; i>-5;i--)

{ n = i*10; printf("i=%4d n=%4d",i,n);

j=0; do {j++; n = n + 10; }

while (!(n == 10)); printf(" j=%4d\n",j);

}

/*

Dany punkt początkowy (0,0) określ algorytm, który symuluje poruszanie się punktu w n = 20 krokach w linii prostej do punktu (20,20). Zmodyfikuj algorytm tak aby punkty pośrednie uwzględniały losowe odchylenie od zadanego kierunku - przyjmij, że wybrany zostanie punkt w obszarze określonym przez daną odległość r . Uwagi: dla r = 0 punkty są na linii prostej ze stałym krokiem o długości r0, losuj funkcją rand ( 0 <= rand < 1 )

Program Marsz;

var

fout1: Text;

i,n:integer;

d,y,r,r0,alf:real;

ax,bx,ay,by:real;

BEGIN

Assign(fout1, 'plo1.dat'); ReWrite(fout1);

randomize;

bx:=20; by:=20; n:=20; r:=1.0;

ax:=0; ay:=0; r0:=bx/n;

x:=ax; y:=ay;

writeln(fout1,x:10:4,y:10:4);

for i:=1 to n do begin

alf :=2*pi*random(100)/100;

x:=x+r0+r*sin(alf);// x:=x+r0+2*r*(random(100)/100.0-0.5);

y:=y+r0+r*cos(alf);// y:=y+r0+2*r*(random(100)/100.0-0.5);

writeln(fout1, x:10:4, y:10:4);

end;

d:=sqrt((x-bx)*(x-bx)+(y-by)*(y-by));

writeln(fout1); close(fout1);

writeln(d:10:4);

END.

http://www.bloodshed.net/devpascal.html

stop

N

n := n -5

T

n

start

n = 5

stop

n: = - n

start

N

w := n > 0

T

n

w

stop

start

N

n :=n +1

T

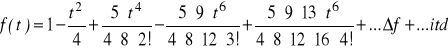
n

pocz

n := n-1

instrukcje2

koniec

N

Szkolka n = n - 5

i= 2 n= 10 j= 1

i= 3 n= 15 j= 2

i= 4 n= 20 j= 3

i= 5 n= 25 j= 4

i= 6 n= 30 j= 5

Szkolka m = m + 5

i= 0 n= 0 j= 1

i= -1 n= -5 j= 2

i= -2 n= -10 j= 3

i= -3 n= -15 j= 4

i= -4 n= -20 j= 5

Szkolka k = k - 10

i= 2 n= 20 j= 1

i= 3 n= 30 j= 2

i= 4 n= 40 j= 3

i= 5 n= 50 j= 4

i= 6 n= 60 j= 5

Szkolka L = L + 5

i= 0 n= 0 j= 1

i= -1 n= -10 j= 2

i= -2 n= -20 j= 3

i= -3 n= -30 j= 4

i= -4 n= -40 j= 5

*/

stop

w

start

N

n :=n+1

T

n

n = n

4.5

wektor 4 elem.,

1 wymiar 4x1

Element

id

X

Y

txt

pE

ciąg 6 elem.,

1 wymiar

3 x 4 x 2 elem.,

3 wymiary

T

3 x 4 elementy,

2 wymiary.

identyfikator, zawartość, adres

zmiennej komórki

2.36

10

12333308

n > 0

instrukcje1

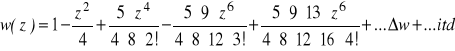
-1e308

i

X

Y

pY

12343292

12343300

12343308

12343316

zmienna

wyrażenie

operacja

podstaw :=

warunek

decyzja

warunek, decyzja

zmienna

start lub nagłówek

stop lub powrót

id

id

n

start

n := n -1

instrukcjeY

stop

n>0N

n<=0

n ? 0

instrukcjeX

start

Petla Go To 5 0 1042.0 631.0

Petla While 0 5 4.0 4.0

Petla Do vA 0 5 4.0 4.0

Petla Do vB 0 5 4.0 4.0

ROZWIAZANE TESTY WYNIKOW

Petla Go To 5 0 1042.0 631.0

Petla While 5 0 1042.0 631.0

Petla Do vA 5 0 1042.0 631.0

Petla Do vB 5 0 1042.0 631.0

n

T

w := n > 0

N

start

n: = - n

stop

n = 5

start

n

T

n := n -5

N

stop

instrukcje1

n > 0

T

N

stop

instrukcje2

n := n -1

start

n

m = 5

start

m

T

m := m + 5

N

stop

L

m

T

L := m > 0

N

start

m: = - m

stop

m = m n 0

m

T

m := m - 2

N

start

stop

instr_a

m > 0

T

N

stop

instr_b

m :=m -1

start

m

instr_1

k > 0

T

N

stop

instr_2

k := k-1

start

k

pf

k

T

pf := k > 0

N

start

k: = - k

stop

k = 10

start

k

T

k := k - 10

N

stop

k = k

k

T

k := k + 2

N

start

stop

instr_A

t > 0

N

T

stop

instr_B

t := t -1

start

t

Q

L

T

Q := L > 0

N

start

L: = - L

stop

L = 5

start

L

T

L := L + 5

N

stop

L = L

L

T

L := L + 2

N

start

stop

n

n = n

A Podaj dla jakich wartości początkowych n iteracje

są skończone.

Określ ich ilość.

B Podaj dla jakich wartości początkowych n iteracje

są skończone.

Określ ich ilość.

C Podaj dla jakich wartości początkowych n iteracje

są skończone.

Określ ich ilość.

	iteracja	b=?	p='⋅'	l=0
	0	U	⋅	1
	1	l	U	1
	2	a	l	1
	3	⋅	a	1
	4	⋅	⋅	1
	5	m	⋅	2
	6	a	m	2
	7	⋅	a	2
	..	..	..	..

d0

r0

p = b

k = 0, p = ' '

nie

tak

tak

b

b ≠ ' ' i

p = ' '

k = k +1

stop

k

nie

r0

r

[-r, r]

[-r, r]

r0

start

r0

r

45^o

r0

r0

r

r

d0

r

45^o

d0

d0

r

r

d_x<|r|

d_y<|r|

d0

d0

E

plo1_4.plt

plot [-2:30] [-2:30] "plo1_4.dat" with lines,0,"y0.dat" with lines

pause -1

gnuplot > load “plo1_4.plt”

0.0000 0.0000

2.4400 0.2000

0.7200 4.3200

.................................

16.6800 17.8000

21.5200 16.7200

24.9200 19.7200

28.7200 19.5200

..............................

36.9200 24.2000

36.2400 21.8400

d_y<|r|

-----------------

n = 16

i1=31,ii1=31,r1=31,s1=31

n = 16

i1=31,ii1=31, r1=31,s1=31

n = 1

i1=1, ii1=1, r1=1, s1=1

---