Temat: Ruch cząstek w jednowymiarowych polach potencjalnych

Lokalne prawa zachowania prawdopodobieństwa

Przyjmijmy, że cząstka o masie m, której stan określa wektor stanu
, porusza się w przestrzeni w niejednorodnym polu potencjalnym
. W reprezentacji położeń jej funkcja falowa
spełnia równanie Schrödingera

. (15.1a)

Funkcja
spełnia równanie

. (15.1b)

Pomnożymy równanie (15.1a) przez
, a równanie (15.1b) przez
i tak otrzymane równania odejmiemy stronami. W rezultacie otrzymamy równanie będące matematycznym sformułowaniem lokalnego prawa zachowania prawdopodobieństwa

. (15.2)

gdzie
jest wektorem gęstości strumienia prawdopodobieństwa

. (15.3)

Przyjmijmy, że ruch cząstki ograniczony jest do obszaru
o objętości
, należącego do przestrzeni R³. Przyj­mijmy, że rozmiary liniowe

obszaru
są jednakowego rzędu
. Obszar
ogranicza powierzchnia
o polu S. Niech
będzie wektorem normalnym do elementu dS tej powierzchni skierowanym na zewnątrz. Scałkujemy obydwie strony równania (15.2) po obszarze

.

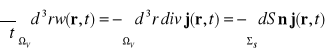
Ponieważ z warunku unormowania funkcji falowej wynika, że

,

więc w tej granicy całkowity strumień prawdopodobieństwa przez powierzchnię S znika, co prowadzi do globalnego prawa zachowania

.

Znając wektor gęstości strumienia prawdopodobieństwa możemy skonstruować gęstości innych wielkości, np. masy
czy ładunku
(e jest ładunkiem cząstki), oraz odpowiednie gęstości strumieni masy
i ładunku
. Te wielkości także spełniają lokalne prawa zachowania.

15.2 Ruch cząstki w nieciągłych polach potencjalnych

Przyjmijmy, że cząstka znajduje się w stanie stacjonarnym o energii E. Wtedy

.

Dla cząstki poruszającej się wzdłuż prostej i będącej w stanie stacjonarnym równanie Schrödingera przyjmuje postać

. (15.1c)

Jest to liniowe, jednorodne równanie różniczkowe zwyczajne drugiego rzędu.

Dalej przyjmijmy, że ruch cząstki odbywa wzdłuż osi x, a także, że funkcja V(x) jest nieciągła, np.

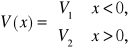
(15.4)

gdzie
. Pokażemy, że z równania Schrödingera (15.1c) wynika ciągłość funkcji falowej i jej pierwszej pochodnej w punkcie
. Scałkujemy obydwie strony równania Schrödingera po x z przedziału
, gdzie ε<<1

.

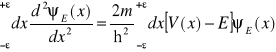
Przepiszemy to równanie w równoważnej postaci

.

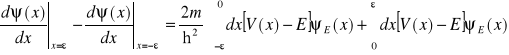
Ponieważ potencjał jest po obydwu stronach stały, gdy w przedziale
funkcja falowa jest powoli zmienna, to

. (15.5)

Gdy potencjał V₂ jest ograniczony, w granicy
prawa strona równania (15.5) znika, stąd wynika warunek ciągłości pochodnej funkcji falowej w punkcie osobliwości potencjału

. (15.6a)

To oznacza, że funkcja falowa w punkcie nieciągłości potencjału nie ma ostrza (punktu kąto­wego) i punktów nieciągłości. Istnienie punktu kątowego związane byłoby z pochodną lewostronną różną od prawostronnej. Łatwo się przekonać, że funkcja falowa także nie po­winna mieć punktów nieciągłości. Rozpatrzymy prosty przykład. Skok potencjału w punkcie
można związać z funkcją schodkową

,

gdzie
jest dystrybucją schodkową Heaviside'a

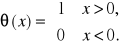
Ponieważ pochodną funkcji schodowej jest dystrybucja delta
, więc

.

To oznacza, że wyrażenie stojące po lewej stronie równania (e5.5) jest nieograniczone, a po prawej - ograniczone. Ostatecznie stwierdzamy, że w punkcie nieciągłości potencjału także funkcja falowa jest ciągła i nie ma punktów kątowych

. (15.6b)

Oczywiście gdy potencjał ma punkt nieciągłości druga pochodna funkcji falowej stanu sta­cjo­narnego nie jest ciągła. Wynika to z równania Schrödingera (15.1c).

15.3 Potencjał w postaci progu

Przyjmijmy we wzorze (15.4)
,
(Rys. 15.1). Wprowadzimy dodatnią stałą

.

W rozważanym zagadnieniu mamy do czynienia z jednym bezwymiarowym parametrem

.

Należy rozważyć dwie możliwości: (A)
, (B)
.

15.3.1 Przelot cząstki mikroskopowej nad progiem potencjału

Gdy
to k jest wielkością rzeczywistą. Ponieważ w przypadku stanów stacjonarnych równanie Schrödingera jest równaniem różniczkowym zwyczajnym drugiego rzędu będziemy poszukiwali rozwiązania równania (15.1c) postaci superpozycji fal płaskich

. (15.7a)

Na lewo od progu
, na prawo od niego
, gdzie

. (15.7b,c)

Zatem

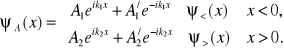
(15.8a)

Na funkcję falową (15.8) nałożymy warunki (15.6), które prowadzą do jednorodnego układu równań liniowych

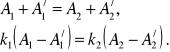
Ten układ równań nie pozwala określić wszystkich stałych. Ich liczbę możemy zmniejszyć używając argumentów ogólnej natury. Przyjmijmy, że źródło cząstek znajduje się z lewej strony daleko od progu
. W obszarze I część
, proporcjonalną do
, możemy uznać za związaną z cząstkami wychodzącymi ze źródła, natomiast część
proporcjonalną do
za związaną z cząstkami odbitymi od progu, bo cząstki rozproszone maja pęd
przeciwnie skierowany do pędu
cząstek padających. Po pra­wej stronie punktu nieciągłości
wyraz
proporcjonalny do
odpowiada czą­stkom, które przeszły z obszaru I do obszaru II. Ponieważ po tej stronie schodka potencjału cząstek odbitych nie ma, a cząstki padają tylko z lewej strony, więc zmuszeni jesteśmy przyjąć, że
. W dalszym ciągu jedna stała nie jest określona (np.
) i pozostałe stałe zależą od niej

. (15.9a,b)

Teraz już możemy podać jawną postać funkcji falowej

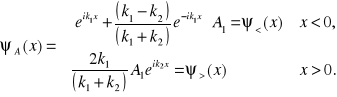
(15.8b)

Nie trudno sprawdzić, że funkcja falowa jest ciągła w punkcie
. Podobnie pochodna funkcji falowej w punkcie nieciągłości potencjału także jest ciągła. Obliczymy gęstość strumienia prawdopodobieństwa dla znalezionego rozwiązania

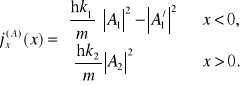
(15.10)

Podstawiając do (15.10) wyrażenia (15.9a,b) otrzymamy jawną postać gęstości strumienia prawdopodobieństwa

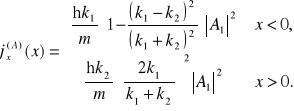
Łatwo sprawdzić, że gęstość strumienia prawdopodobieństwa jest w punkcie nieciągłości potencjału ciągła. Dla
pierwszy wyraz wzoru (15.10),
, odpowiada czą­stkom padającym, a drugi
- odbitym. Natomiast dla
wkład dają tylko cząstki przepuszczone, zatem
. Wprowadzimy współczynniki odbicia
i przepuszczania (transmisji) T

,
(15.11a,b)

Dla rozwiązania (15.10) mamy

,
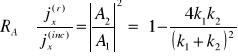
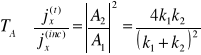
. (15.12a,b)

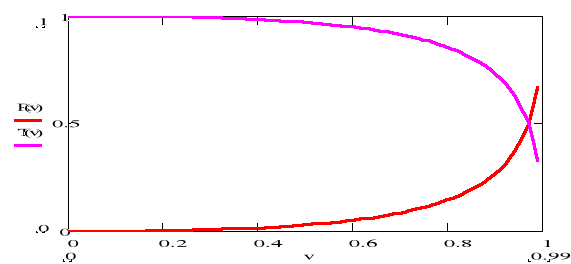
Rys. 15.2

Ponieważ gęstość strumienia prawdopodobieństwa jest wielkością ciągła wprowadzone współczynniki spełniają warunek bilansu strumienia prawdopodobieństwa
. W rozważanym zagadnieniu zachowanie się cząstek jest niezgodne z fizyka klasyczną, gdyż gdy energia cząstek jest większa od energii progu
wszystkie padające cząstki powinny znaleźć się w obszarze
. Cząstki odbite nie powinny pojawić się w ogóle. Współczynniki T_A i R_A zależą jedynie od parametru
. Ich zależność od v przedstawia Rys. 15.2.

,
.

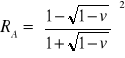
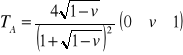
Zbadajmy jak zachowują się współczynniki T_A i R_A w granicy
. Ponieważ
więc
,
. Wynik ten jest zgodny z intuicją. Ponieważ nie ma nieciągłości potencjału, nie ma cząstek odbitych
i wszystkie cząstki zostają przepuszczone
.

15.3.2 Odbicie cząstek mikroskopowych od progu potencjału

Rozpatrzymy przypadek (B) gdy
. Zgodnie z fizyką klasyczną pojawienie się cząstek w obszarze
jest niemożliwe. Tym razem
, zatem roz­wią­za­nie równania Schrödingera, które znika gdy x rośnie nieograniczenie, ma postać

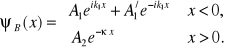
(15.13a)

Z warunków ciągłości funkcji falowej i jej pierwszej pochodnej znajdujemy współczynniki

,
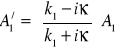
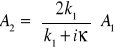
. (15.14)

Wprowadzimy kąt

. (15.15)

Wyrazimy fazę
przez parametr

.

Zależność fazy δ od parametru v pokazuje Rys. (15.3). Związek (15.15) oznacza, że k₁ i κ są ze sobą związane, a współczynniki
różnią się czynnikiem fazowym

,
. (15.16a,b)

Zapiszemy rozwiązanie (15.13a) dla
wykorzystując związek (15.16b)

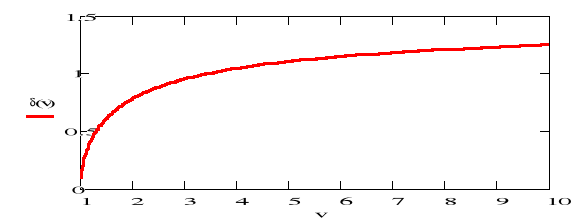
Rys. 15.3

. (15.17)

Wspólny czynnik fazowy jest nieistotny. Jak widać fazy fali odbitej i padającej różnią się o
, co spowodowane jest wnikaniem cząstek w obszar wzbroniony w fizyce klasycznej. Interferencja amplitud prawdopodobieństwa fali dla cząstek padających i odbitych daje w wyniku falę stojącą. Gdy
(tzn.
) to
, a więc wtedy różnica faz gęstości amplitud prawdopodobieństwa cząstek padających i odbitych wynosi
.

Dla
gęstość strumienia prawdopodobieństwa znika, bo jest różnicą dwóch iden­tycznych wyrazów. Podobnie znika ona z lewej strony nieciągłości potencjału bo
. Zatem w rozważanym przypadku
. Takie zachowanie się strumienia z lewej strony punktu nieciągłości potencjału wynika z kompensacji strumieni cząstek pa­da­ją­cych i odbitych, czego matematycznym wyrazem jest utworzenie fali stojącej (15.13a), dla której propagacja fali jest nieobecna. Obliczymy współczynnik

.

Znikanie strumienia po prawej stronie nieciągłości potencjału nie oznacza, że cząstki nie wni­kają do tego obszaru. Rzeczywiście gęstość prawdopodobieństwa znalezienia cząstki w stanie charakteryzowanym przez wektor
w obszarze
równa jest
i za­nika wykładniczo z rosnącym x. Gdy
to
więc dla wszystkich

. Oprócz tego Gdy
to
i
. Po prawej stronie nieciągłości funkcja falowa znika wszędzie włączając punkt
, w punkcie
funkcja falowa także znika, a więc i w tym granicznym przypadku funkcja falowa jest ciągła. Lecz ponieważ warunek (15.5) nie jest spełniony (bo potencjał jest nieograniczenie duży) w punkcie nieciągłości potencjału gęstość strumienia prawdopodobieństwa nie jest ciągła.

Obliczymy energię lokalizacji cząstki wewnątrz obszaru
. Cząstki wnikają weń na odległość
rzędu
. Zatem nieoznaczoność pędu
jest rzędu
, a nieozna­czo­ność energii
(energia lokalizacji cząstki) jest rzędu

.

Jak widać próba ustalenia czy cząstka znajduje się na lewo od punktu
powoduje zabu­rzenie stanu cząstki, którego wyniku cząstka przestaje znajdować się w stanie stacjonarnym. Zatem zgodnie z zasadą superpozycji istnieje nieznikające prawdopodobieństwo, że cząstka ma energię większą od wysokości progu. W wyniku tego zaburzenia całkowita energia cząstki

.

wystarcza aby cząstki mogły penetrować obszar niedostępny w ramach fizyki klasycznej.

15.3.3 Rozproszenie cząstek na progu potencjału

Rozpatrywaliśmy stacjonarny strumień cząstek wysyłanych z nieskończenie odległego źródła znajdującego się z lewej strony obszaru, w którym potencjał nie znika. W wyniku oddziały­wania z polem potencjalnym padające cząstki zmieniają stan ­ zmieniają się ich pędy. Mówi­my, że cząstki ulegają rozproszeniu. Gdy rozproszenie nie powoduje zmiany energii cząstek padających mówimy, że jest sprężyste. Nasze wyniki wskazują na to, że gdy potencjał
znika stan cząstek nie ulega zmianie - nie ma rozproszenia.

Rozważymy przypadek B. Zapiszemy funkcję
w postaci

, (15.18)

gdzie współczynnik
jest macierzą rozproszeń dla naszego bardzo prostego przykładu. Macierz rozproszeń zależy od charakterystyk potencjału rozpraszającego - w naszym prostym przypadku od wysokości stopnia V₀. Określa ona zdolność potencjału do rozpraszania cząstek. Dla rozważanego przypadku

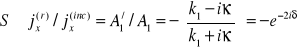
. (15.19)

Prawo zachowania prawdopodobieństwa wymaga by
. W przypadku gdy macierz rozproszeń ma więcej elementów niż jeden jest to warunek unitarności. W drugiej postaci funkcji
(15.18) wydzieliliśmy wkłady pochodzące od wkładu nie zaburzonego przez potencjał ruchu cząstek rozchodzących się ze źródła
i schodzących się do niego
cząstek oraz wkład związany z rozproszeniem
. Można sprawdzić, że macierz rozproszeń (15.19) spełnia jeszcze dwa związki

,
. (15.20)

wynikają one z bardzo ogólnych własności równania Schrödingera.

15.4 Oddziaływanie cząstek mikroskopowych z barierą potencjału

Przyjmijmy, że potencjał
ma postać (Rys. 15.4)

. (15.21)

Barierę potencjału charakteryzują trzy parametry

E,
i
, (15.22a,b)

gdzie E_l jest energią lokalizacji cząstki w obszarze bariery

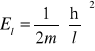
. (15.22c)

Jak widać wysokość V₀ bariery wyrażać będziemy w jednostkach energii cząstki. Podobnie zamiast grubości bariery l będziemy używali energii lokalizacji E_l wyrażonej w jednostkach energii cząstki.

15.4.1 Przelot cząstki mikroskopowej nad barierą

Przyjmijmy dalej , że
, wtedy fizyka klasyczna nie nakłada ograniczeń na ruch cząstek. Jak w przypadku A (§ 15.3) będziemy szukali rozwiązania równania Schrödingera w postaci

, (15.23a)

gdzie

, (15.23b,c,d)

natomiast wektory falowe
określają wzory (15.7b,c).

Warunki ciągłości funkcji falowej i jej pochodnej w miejscach nieciągłości potencjału dają układ czterech równań dla pięciu niewiadomych, a więc rozwiązania zależą od jednej z nich, np.
. Wypiszemy odpowiednie równania

, (15.24a,b)

, (15.24c,d)

i dwa z ich rozwiązań

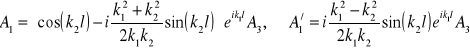
. (15.25a,b)

Znajomość tych dwóch współczynników pozwala obliczyć przy pomocy wzorów (15.11a,b), współczynniki odbicia i przepuszczania

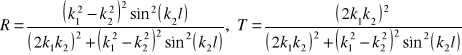
, (15.26a,b)

Ich suma równa jest jedności. Wyrazimy współczynnik przechodzenia przez
i E

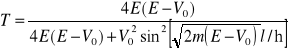
. (15.27)

Zauważymy, że gdy
to
więc
. Jest to zachowanie zgodne z intuicją.

Współczynnik przejścia jest okresową funkcją grubości bariery l. Dla

osiąga on wartości maksymalne równe 1, a dla

- wartości minimalne
. Dla grubości l spełniających warunek rezonansu T=1, a więc bariera potencjału jest zupełnie przezroczysta - w ogóle nie stanowi przeszkody dla cząstek.

Wyrazimy współczynniki R oraz T przez parametry bezwymiarowe v oraz ε (15.22a,b)

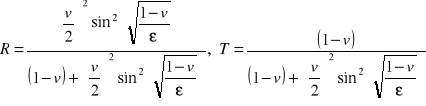
. (15.26c,d)

Zależność tych współczynników od v oraz ε w szerokim zakresie parametrów przedstawia Rys. (15.5a,b). Na Rys. 15.6a,b tak zakres zmienności parametrów został tak wybrany by były widoczne oscylacje ich wielkości.

Pokażemy, że gęstość strumienia prawdopodobieństwa jest wielkością ciągłą. W obszarze III wzór (15.5) dla funkcji falowej
(15.23d) prowadzi do prostego wyniku

. (15.28)

W obszarze I wypadkowa gęstość strumienia wynika ze wzoru (15.3) i jest równa

.

Po podstawieniu za
i
wyrażeń (15.24a,b) i prostych przekształceniach otrzymamy
, a więc
. Na koniec znajdziemy gęstość strumienia prawdo­podo­bieństwa w obszarze II. Z. równań (15.23c,d) znajdujemy współczynniki

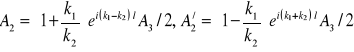
. (15.28a,b)

Funkcji falowej
(15.22c) odpowiada gęstość strumienia prawdopodobieństwa

Po podstawieniu za
wyrażeń (15.28a,b) otrzymamy
. Sprawdziliśmy, że strumień gęstości prawdopodobieństwa jest jednakowy we wszystkich trzech obszarach osi x.

15.4.2 Tunelowanie cząstek mikroskopowych przez barierę potencjału

Zbadajmy rozwiązania stacjonarnego równania Schrödingera gdy
. Nie musimy prowadzić rachunków od początku. Wystarczy zauważyć, że w tym przypadku

,

a więc funkcja falowa wewnątrz bariery potencjału ma postać

.

Po zamienieniu we wzorach (15.25) k₂ na
znajdziemy współczynniki A₁ i

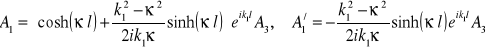
. (15.29)

To pozwala znaleźć współczynnik przepuszczania i odbicia

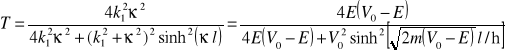
. (15.30a)

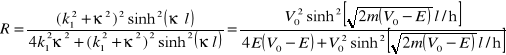
. (15.30b)

Gdy
współczynnik przepuszczania wykładniczo maleje

.

Zbadamy zachowanie się współczynników T i R gdy wysokość bariery V₀ albo jej grubość l rośnie nieograniczenie

,

.

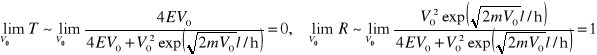
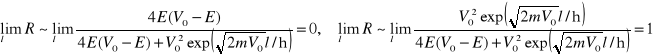
Jak widać dla bardzo wysokiej albo bardzo grubej bariery gęstość amplitudy prawdopodobie­ństwa cząstek przepuszczonych znika natomiast odbitych - osiąga maksimum.

Wyrazimy współczynnik odbicia R i przepuszczania T przez parametry v
oraz ε

,
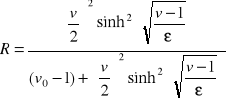
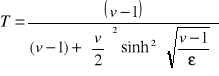
. (15.31a,b)

Zależność współczynników odbicia i przepuszczania od parametrów v i ε przedstawia Rys. (15.7a,b)

Zjawisko tunelowania jest konsekwencją równania Schrödingera - jest ono przejawem „wyciekania” i „wciekania” (15.30b) amplitud prawdopodobieństwa. Założenie o istnieniu tego zjawiska stanowiło punkt wyjściowy heurystycznego wyprowadzenia równania Schrödingera podanego w R. 14. Zjawisko tunelowania jest powszechnie obserwowane w fizyce układów mikro­sko­powych, np. jego przejawem jest rozpad α jąder atomowych. Zjawisko tunelowania jest często wykorzystywane w urządzeniach nowoczesnej elektroniki [3].

Literatura:

[1] C. Cohen-Tannoudji, B. Diu, F. Laloë, Quantum Mechanics, Vol. 1,Willey New York & Hermann, Paris, 1977, Complement H_I, str. 67

[2] G. Baym, Lectures on Quantum Mechanics, Benjamin, Reading, Mass., 1974, R. 4.

[3] Gerard Milburn, Inżynieria kwantowa, Prószyński i S-ka, Warszawa 1999.

Szukasz gotowej pracy ?

To pewna droga do poważnych kłopotów.

Plagiat jest przestępstwem !

Nie ryzykuj ! Nie warto !

Powierz swoje sprawy profesjonalistom.

---