Ekonometria to:

• to nauka o mierzeniu zjawisk ekonomicznych (dosłownie)

• nauka o mierzeniu związków występujących między procesami ekonomicznymi a innymi zjawiskami np. społecznymi, przyrodniczymi, technicznymi, demograficznymi itp.(dokładnie)

• określenie wszelkich zastosowań metod statystycznych i matematycznych do rozwiązywania zagadnień ekonomicznych (szeroko)

• (wg O. Lange) - nauka zajmująca się ustalaniem za pomocą metod statystycznych konkretnych, ilościowych prawidłowości zachodzących w życiu gospodarczym (klasycznie)

Ekonometria menedżerska

Ekonomia menedżerska - formułuje podstawy decyzji podejmowanych w przedsiębiorstwie.

Ekonometria menedżerska - nauka o mierzeniu związków występujących między zjawiskami ekonomicznymi a innymi zjawiskami w procesie podejmowania decyzji w przedsiębiorstwie.

Rozszerzenie definicji O. Langego - Ekonomia menedżerska - nauka zajmująca się ustalaniem za pomocą metod statystycznych i matematycznych, konkretnych ilościowych prawidłowości zachodzących w życiu gospodarczym, w celu określenia warunków i czynników wyznaczających optymalne decyzje.

Model ekonometryczny

(wg Z. Czerwińskiego) - może być rozumiany ogólnie, intuicyjnie jako obraz, odbicie, odwzorowanie określonego obiektu w określonym języku.

Model ekonometryczny - również będzie układem równań odwzorowującym wyróżnione zależności między zjawiskami ekonomiczno - społecznymi.

Część związków można mierzyć a niektóre nie.

Związki mierzalne nazywane są korelacyjnymi.

Y = f (x₁, x₂ ......x_kς)

y - zjawisko badane

x₁,x₂-zjawiska, czynniki

ς- składnik losowy (psi,) - jest to łączny efekt oddziaływania na zmienną y, oddziałuje na te i inne czynniki, które nie zostały uwzględnione bezpośrednio w zbiorze x.

Jest to zmienna losowa o określonym rozkładzie.

E(ς) = 0; D²(ς) = δ² = const. (δ² - wariancja)

Wg S. Bartosiewicza- model ekonometryczny to ustalona stochastyczna zależność wyróżnionego lub wyróżnionych zjawisk ekonomicznych od zjawisk czynników. Formułuje układ funkcji (lub funkcja) na ogół wielu zmiennych aproksymujących z pewną dokładnością opisywany fragment rzeczywistości ekonomicznej.

Składniki modelu:

• Zmienne,

• Parametry,

• Składnik losowy.

Zmienne w modelu dzielimy na:

• Endogeniczne - objaśniane przez poszczególne równania modelu {y};

• Objaśniające

• egzogeniczne - objaśnia kształtowanie się zmiennych endogenicznych, same przez model objaśniane nie są {x_i}. Wśród nich może być zmienna czasowa „t”.

• zmienne opóźnione lub z wyprzedzeniem czasowym np.(x_it-1, x_it-2, .......x_it-s, y_t-1).

Parametry związane są z konkretną postacią analityczną modelu

• Model liniowy

y_t=α₁x_1t + α₂x_2t +...............+ α₀ς_t

α_i = ( i=1,2.... k) - parametry strukturalne, od nich zależy wartość funkcji opisującej kształtowanie się zmiennej endogenicznej.

a_i - oszacowanie parametrów α_i (zmienna losowa).

Parametry struktury stochastycznej modelu - to parametry rozkładu składnika losowego ς_t np. E(ς_t), D²(ς_t), ρ(ς_t, ς_t-s) - (współczynnik korelacji modelu)

Klasyfikacja modeli ekonometrycznych.

Wg modelów poznawczych.

1. Przyczynowo - skutkowe (przyczynowo - opisowe).

Zmienna endogeniczna x jest obiektywną przyczyną kształtowania się zmiennej y. Model taki ma największe walory poznawcze.

2. Symptomatyczne -wyglądają jak te wyżej. Zmienne x są zmiennymi silnie skorelowanymi ze zmienną endogeniczną. Przykładem może być zależność między dochodem narodowym a liczbą ludności w wieku produkcyjnym.

3. Tendencji rozwojowych - modele, w których mamy jedną zmienną (zmienna czasowa t) i ten model opisuje mechanizm rozwoju zjawisk w czasie. Budowane są głównie w celach produktywnych budowy prognoz).

4. Autoregresyjne - zmienna y jest opisywana przez funkcje samych siebie z okresów poprzednich za jego pomocą można przedstawiać inwestycje.

Modele od 1 do 4 zakładają, że struktura ekonomiczna, którą opisują jest stała.

5. Adaptacyjne - budowane są w ten sposób, że w miarę powstawania nowych informacji ten model budowany jest na nowo.

Modele są wykorzystywane w celach poznawczych do prognoz i podejmowania decyzji.

Etapy budowania modelu

1. Sprecyzowanie przedmiotu badania - wybór zjawiska badanego.

2. Specyfika równań modelu

• Zmienne (analiza merytoryczna)

• Postać analityczna (analiza merytoryczna i formalna).

3. Zbieranie danych statystycznych.

4. Analiza własności wybranych zmiennych (analiza formalna) m.in.

• Zmienność wartości;

• Symetria rozkładu;

• Stopień skorelowania z innymi zmiennymi.

5. Estymacja parametrów strukturalnych modelu;

6. Weryfikacja modelu, ocena dokładności opisu badanego zjawiska.

7. Wykorzystanie modelu np. do wnioskowania w przyszłość lub symulacji zachowania badanego zjawiska w określonych warunkach.

Metoda nośników informacji (Z. Helwiga).

y - zmienna objaśniana

x_j - potencjalna zmienna objaśniająca j = 1,2 .... k

Dana jest macierz obserwacji na wszystkich zmiennych , n - liczba obserwacji

Na podstawie tych obserwacji obliczamy elementy wektora R_o , który zawiera współczynnik korelacji pomiędzy zmienną y a poszczególnymi zmiennymi.

R₀ =
= [r_j] j=1,2,,,,,k

r_j - współczynnik korelacji liniowej zmiennych y, x_j

R - macierz zawierająca współczynnik korelacji pomiędzy parametrami x i potencjalną zmienną objaśniającą j.

R =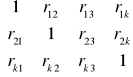
= j =1,2, ,k; i = 1,2,, k = [r_ij]

r_ij= współczynnik korelacji liniowej zmiennych x_i y_j

Liczba kombinacji zmiennych objaśniających

L=2^k-1

np. k =3 → L= 2³-1 = 7

Kombinacje:

1) x₁ 2) x₂ 3) x₃

4) x₁; x₂ 5) x₁; x₃ 6) x_2; x₃

7) x₁; x₂; x₃

x_j - nośnik informacji

j-ta - kandydatka na zmienną objaśniającą.

Pojemność indywidualna j-tego nośnika informacji w l-tej kombinacji

h_lj=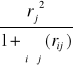

h_lj = 1, 2, ..... k

l = 1, 2, ... (2^k - 1)

h_lj Є [0,1]

Interesuje nas czy jest to korelacja dodatnia czy ujemna

Najlepszy będzie ten zbiór, który będzie miał największą sumę pojemności indywidualnych.

Pojemność integralna kombinacji nośników

H_i=
H_i Є [0,1]

k_l - liczba zmiennych wchodzących w skład badanej informacji.

Kombinacja optymalna

H_l = max H_l

Wykład 28.04.2001r.

Przykład

Biuro podróży działające w pewnym mieście przeprowadziło badania współzależności pomiędzy rocznymi wydatkami na turystykę zagraniczną Y_t (w 100 zł na osobę) a przeciętnym dochodem x_1t (w 100 zł na osobę w rodzinie), liczbą dzieci w rodzinie x_2t i przecietną ceną wycieczki x_3t w 100 zł . Na podstawie wyników badania ankietowego obliczono następujące współczynniki korelacji pomiędzy wyróżnionymi zmiennymi:

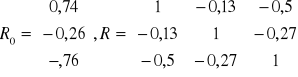
Stosując metodę Hellwiga wybrać optymalną kombinację zmiennych objaśnianych kształtowanie się wydatków na podróże zagraniczne.

K=3

Badane podzbiory zmiennych:

1. {X_1t}

2. {X_2t}

3. {X_3t}

4. {X_1t, X_2t}

5. {X_1t; X_3t}

6. {X_2t; X_3t}

7. {X_1t; X_2t; X_3t}

L=2^k-1=8-1=7

Pojemność indywidualna nośnika informacji j w l-tej kombinacji:

H_lj=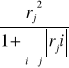
pojemność indywidualna

L = 1,2,.........7, i,j = 1,2,3

Pojemność integralna = suma pojemności indywidualnych

H_l=

Kombinacja optymalna

H_opt= max₁H₁

Obliczenia

1. h₁₁ = r1²= (0,74)² = 0,5476

2. h₂₂=r2² = (-0,26)²=0,0676

3. h₃₃=r3²=(-0,76)²=0,5776

4. h₄₁=
   

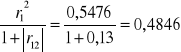
h₄₂=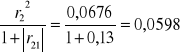

5. h₅₁=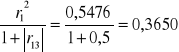

h₅₃=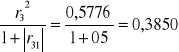

6. h₆₂=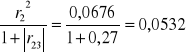

h₆₃=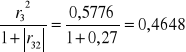

7. h₇₁=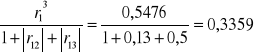

h₇₂=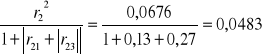

h₇₃=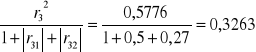

H₁=0,5476

H₂=0,0676

H₃=0,5776

H₄=h₄₁+h₄₂=0,4846+0,0598=0,5444

H₅=h₅₁+h₅₃=03650+0,3850=0,75

H₆=h₆₂+h₆₃=0,0532+0,4548=0,508

H₇=h₇₁+h₇₂+h₇₃=0,3359+0,0483+0,3263=0,7105

H_opt=H₅

X_opt={X_1t, X_3t}

Model

Y_t=α₁x_1t+α₂x_3t+α₀+ς_t

Lub

Y_t=α₁x_1t+β₂x_3t+γ+ς_t

Dalszy etap budowy modelu:

Funkcja potęgowa wykorzystywana jest przy modelowaniu produkcji, popytu, podaży.

Y_t=α₀+x₁^α +α₂^α+ ..........

Mogą być inne postacie analityczne niż liniowe

Etap estymacji parametru modelu

Estymacja - przypisywanie nieokreślonym dotąd parametrom konkretnych wartości liczbowych. Wykorzystuje się w tym celu informacje o realizacjach zmiennych y_t i x_t

Metoda najmniejszych kwadratów MNK

MNK polega na znajdowaniu takich wartości ocen parametrów strukturalnych modelu, by suma kwadratów odchyleń zaobserwowanych (empirycznych) wartości i zmiennej y, od jej wartości teoretycznych wyznaczonych przez model była najmniejsza w przypadku jednej zmiennej objaśniającej.

MNK polega na znajdowaniu takiej prostej , która jest najlepiej dopasowana, do wszystkich punktów empirycznych, czyli minimalizowana jest sumą kwadratów reszt (u_t).

Reszta modelu u_t = y_t - y_t^* = y_t - a₁x₁ - a₀

y_t^* - wartość teoretyczna, wartość wyliczona z modelu.

Oznaczenia

Model

y_t =

Model oszacowany

y_t=

Reszta modelu

u_t = y_t - y_t^* = y_t -
= y_t - α₁x_1t - αx_2t - α₃x_3t - ............- u₀

Zapis macierzowy

Model y = x_α+ς x_kt=1

Model oszacowany y = x_a + u

Wektor reszt u = y - x_a

Y(n_x1) x(n_x1) α(n_x1) a(n_x1) ς(n_x1) u(n_x1)

α - wektor prawdziwych parametrów modelu.

Warunek MNK

Q=

Czyli

Q= u^t u = (y - x_a)^t- (y - x_a) = min

Q= y^ty-2y^txa + a^tx^txa = min

warunek konieczny - minimum

stąd

x^ty = x^tx_a x^tx - dodatnie określany

a = (x^tx)^-1x^ty

warunek dostateczny minimum

x)

w punkcie a=(x^tx) funkcja a ma ekstremum minimum

Klasyczne założenia MNK

1. Zmienne objaśniające x są nielosowe i niewspółliniowe k<n;

2. Istnieje n populacji składników losowych, o nadziejach matematycznych E(ς_t)=0 i stałych wariancjach o skończonych wartościach δ² =D²(ς_t) = const, t= 1, 2, 3, ...... n

3. Realizacje zmiennych tworzą proces czysto losowy tzn., że następuje po sobie realizacja składnika losowego , są nieskorelowane, czyli ρ(ς_t; ς_ts)= 0 dla t ≠ s

4. składniki losowe są nieskorelowane ze zmiennymi objaśniajacymi.

Jeżeli ww. założenia są spełnione to estymator ma dobre własności tzn.

1. jest nieobciążony;

2. zgodny;

3. najbardziej efektywny;

Nieobciążoność estymatora polega na tym, że średnia wartość jest równa prawdziwemu parametrowi

Nieobciążoność - „a”

E(a) = α

Estymator zgodny to taki, w którym przy n rosnacym prawdopodobieństwo popełnienia błędu szacunku maleje

Najbardziej efektywny to estymator obarczony jest najmniejszym błędem

Ocena rzędu dokładności otrzymanych ocen parametrów.

Błędy średnie szacunku

1. Błąd szacunku i-tego parametru

a_i-α_i

2. Macierz wariancji i kowariancji estymatorów

D²(a) = δ²(x^Tx)^-1

D(a) =

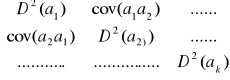
3. Wariancja estymatora i-tego parametru

D²(a_i)=δ²-e_ij

jest miarą dokładności oszacowań

e_ij - i-ty element diagonalny macierzy (x^Tx)^-1

5. Błąd średni szacunku i-tego parametru

D(a_i) =

Dla dowolnego parametru

α_i ≈ a_i ± D(a_i)

Nieobciążoną oceną wariancji składnika losowego jest wariancja resztowa

S²=
n_t = y_t - y_t^*

* - wariancja kosztowa

S²=

S - odchylenie resztowe, odchylenie standardowe reszt.

S=

Nieobciążona ocena wariancji estymatora parametru α_i

d²(a_i) = S²C_ii

Średni błąd estymatora i-tego parametru

d(a_i) = S

Dla dowolnego parametru α_i mamy

α_i ≈ a_i ± d(a_i)

Model oszacowany

Y_t=a₁x_1t + a₂x₂₁+..............................+a_kx_kt+u_t

Miary zgodności modelu z danymi empirycznymi

1. odchylenie standardowe reszt - s

s =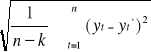

s - informuje o ile średnio rzecz biorąc zaobserwowana wartości zmiennej endogenicznej

odchylają się od wartości wyznaczonych na podstawie oszacowanego modelu

2. współczynnik zmienności przypadkowej - w

w -informuje jaki procent wartości zmiennej objaśnionej modelu, stanowi odchylenie

resztowe

Dla modelu liniowego oszacowanego, MNK mamy:

1. 
   
   

2. 
   

3. współczynnik zbieżności
   

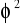
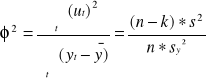
- wskazuje jaka część całkowitej zmienności zmiennej endogenicznej stanowi

zmienność niewyjaśniona przez model, zmienność przypadkowa

4. współczynnik determinacji R²

R²=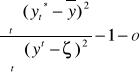

R²
(0,1) wskazuje jaką część całkowitej zmienności zmiennej y, stanowi zmienność wyjaśniona przez model, zdeterminowana przez zmienne objaśniające.

Skorygowany współczynnik determinacji

Eliminacje wpływu ilości zmiennych objaśniających na wartość współczynnika determinacji.

Wykład 29.04.2001r.

Przykład

W 10 kolejnych okresach stwierdzono następujące przeciętne wielkości zatrudnienia X₁ (w tys. osób), produkcji wyrobu X₂ (w tys. sztuk) oraz całkowitych kosztów produkcji Y (mln. zł.)

t	Yt	X1t	X2t	X1t^2	X1t*x2t	X1t*yt	X1t*yt	X2t*yt	Yt^2
1	350	0,7	10	0,49	100	7	245	3500	122500
2	352	0,8	11	0,64	121	8,8	281,6	3872	123904
3	357	0,9	11	0,81	121	9,9	321,3	3927	127449
4	350	0,9	10	0,81	100	9	315	3500	122500
5	364	0,9	13	0,81	169	11,7	327,6	4732	122496
6	365	1,1	12	1,21	144	13,2	401,5	4380	133225
7	364	1,1	12	1,21	144	13,2	400,4	4368	132496
8	371	1,2	14	1,44	196	16,8	445,2	5194	137641
9	376	1,2	14	1,44	196	16,8	451,2	5264	141376
10	371	1,2	13	1,44	169	15,6	445,2	4823	137641
Σ	3620	10	120	10,3	1460	122	3634	43560	1301228

Σx₁ Σx²₁

Model

gdzie X_(10x3) ; Y_(10x1) n = 10

;
;

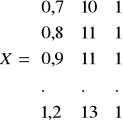
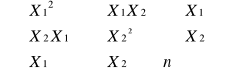
Wyznacznik macierzy

wg La'Plasa

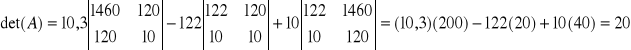
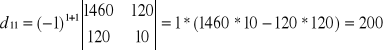
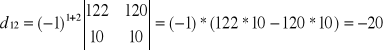
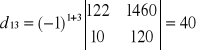
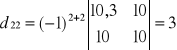
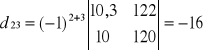
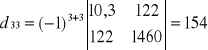
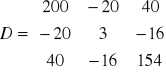
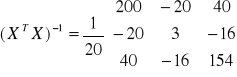
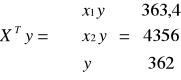
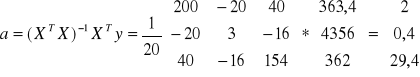
Model oszacowany

• Jeżeli zatrudnienie wzrośnie o 1000 osób to przeciętne koszty całkowite wzrosną o 2 *10 mln zł.,x₂ nie ulegnie zmianie

• Jeśli wielkość produkcji wzrośnie o 1000 szt. , spowoduje to wzrost kosztów o(0,4*10 mln) 4 mln zł. przy założeniu , że zatrudnienie nie ulegnie zmianie

Sprawdzamy czy model jest dostatecznie dokładny. Przeprowadzamy etap weryfikacji modelu. Od wariancji resztowej odejmujemy miernik określający dokładność danych

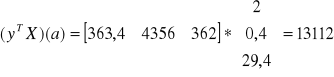
Błąd średni szacunku

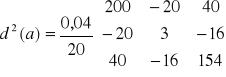
d(a₁)= 0,632

d(a₂)= 0,077

d(a₃)= 0,555

(0,632) (0,077) (0,555)

Gdybyśmy wielokrotnie liczyli ten parametr to średni błąd wyniósł by ± 0,632

W jakim stopniu model został dopasowany do danych empirycznych:

- przeciętna wielkość

wartości liczone z modeli różniły by się przeciętnie o ± 0,2 mln zł

Współczynnik zmienności przypadkowej

Współczynnik zbieżności

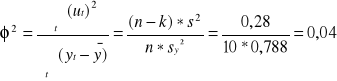
zmienność przypadkowa nie wyjaśniona przez model stanowi 4% zmienności Y

lub

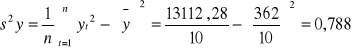
Współczynnik determinacji

= 96% - model opisuje koszty całkowite w 96 %

- wskazuje jaką część całkowitej zmienności zmiennej y_t stanowi zmienność wyjaśniona przez model, zdeterminowana przez zmienne wyjaśniające (jaka część y została zdeterminowana przez model).

Testowanie hipotez statystycznych

Hipoteza statystyczna - dowolne przypuszczenie co do rozkładu populacji generalnej (jego postaci funkcjonalnej lub wartości parametrów)Prawdziwość tego przypuszczenia jest oceniana na podstawie wyników z próby losowej.

Test statystyczny - reguła postępowania, która każdej możliwej próbie przyporządkowuje decyzje przyjęcia lub odrzucenia hipotezy. Jest to reguła rozstrzygająca jakie wyniki z próby pozwolą uznać sprawdzoną hipotezę za słuszną , a jakie za fałszywą.

Zasady budowy testu

1. Formułowanie hipotezy podlegającej weryfikacji H₀ oraz hipotezy alternatywnej H₁, będącej zaprzeczeniem hipotezy sprawdzanej , którą przyjmujemy za prawdziwą kiedy odrzucamy H₀.

2. Określenie obszaru przestrzeni próby, takiego, że jeśli wynik z próby znajduje się w tym obszarze , to sprawdzona hipotezę zerową odrzucamy, a jeśli nie to hipotezę przyjmujemy. Obszar ten nazywa się obszarem odrzucenia hipotezy lub kryterium testu.

3. Definiowanie i obliczanie wartości statystycznych z próby nazywamy sprawdzeniem hipotezy. Wartość ta jest podstawą decyzji o przyjęciu lub odrzuceniu hipotezy.

4. Ustalenie poziomu istotności α, czyli prawdopodobieństwa popełnienia błędu polegającego na odrzuceniu hipotezy prawdziwej.

Test „F”

H₀ : α₁ = α₂ = ............. α_k = 0 (z wyjątkiem wyrazu wolnego)

H₁ : przyjmujemy jeden z parametrów α_i ≠ 0

Jeżeli Y ma rozkład normalny to sprawdzian hipotezy jest dany wzorem:

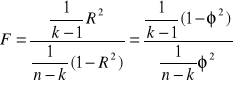
F - ma rozkład Fischera-Snadecora o k-1 i n-k stopniach swobody

Jeżeli dla założonego α

F > F_α to H₀ odrzucamy

Badanie istotności parametrów strukturalnych

H₀ : α_i = 0 hipoteza sprawdzana

H₁ : α_i ≠ 0 hipoteza alternatywna

Sprawdzianem hipotezy jest zmienna t

- sprawdzian hipotezy

t_i - ma rozkład Studenta o (n-k) stopniach swobody

t_α - wartość zmiennej t dla poziomu istotności α i n-k stopni swobody

Gdy

to H₀ odrzucamy

Gdy
to nie ma podstaw do odrzucenia

Estymacja przedziałowa

Estymacja przedziałowa - szacowanie nieznanych wartości parametrów poprzez podanie przedziałów liczbowych, w których zakłada się, że będą zawierać prawdziwe wartości poszukiwanych parametrów z ustalonym z góry prawdopodobieństwem

γ = 1- α

gdzie: γ - to współczynnik ufności

Przedział ufności dla parametru α_i

P{a_i - t_αd(a_i) < α_i < a_i + t_αd(a_i)}= γ

t_α - wartość krytyczna dla zmiennej losowej w rozkładzie t - Studenta dla n - k stopni swobody przy ustalonym poziomie ufności α

Test F

H_o : α₁ = α₂ = α₃ = 0

H₁ : przyjmujemy jeden z parametrów α_i ≠ 0

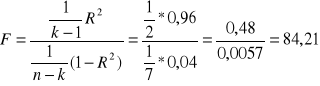
- poziom istotności

odrzucamy

Badamy poszczególne parametry za pomocą t-Studenta

Istotność parametrów strukturalnych modelu

H_o : α₁ = 0

H₁ : α₁ ≠ 0

dla
i przy
;

H₀ odrzucamy na korzyść H₁ 3,1646 > 2,365

H_o : α₂ = 0

H₁ : α₂ ≠ 0

H₀ odrzucamy na korzyść H₁

H_o : α₃ = 0

H₁ : α₃ ≠ 0

H₀ odrzucamy na korzyść H₁

Wszystkie parametry są statystycznie istotne.

Właściwości rozkładu reszt modelu

Reszty w dobrym modelu powinny :

1. być losowe

2. mieć symetryczny rozkład

3. nie powinny być między sobą skorelowane (żądamy by nie występowała autokorelacja reszt)

4. wariancje składowych losowych i reszt powinny być stałe (jednorodne) - stabilność wariancji

5. normalność

Gdy powyższe warunki są spełnione mówimy, że estymator ma dobre własności.

Do badanie losowości wykorzystuje się test serii.

Test serii

H₀ : reszty modelu są losowe

H₁ : reszty modelu nie są losowe

Oznaczenia:

A gdy n_t > 0

B gdy n_t < 0 gdy n_t = 0 pomijamy

C - empiryczna liczba serii

n₁- liczba reszt dodatnich

n_α- liczba reszt ujemnych

Dla poziomu istotności
i
odczytujemy z tablic odpowiednio C₁ i C₂

Jeżeli C₁ < C < C₂ to H₀ nie ma podstaw do odrzucenia

Jeżeli C
C₁ lub C
C₂ to H₀ odrzucamy

Wykład 13.05.2001r.

Symetria reszt

H₀ - reszty są symetryczne

H₀ :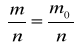

H₀ :
m - liczba reszt dodatnich

H₁ :
n - liczba obserwacji

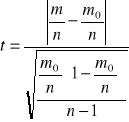
gdy n
30 to „t” ma rozkład studenta o n-1 stopniach swobody

n > 30 rozkład normalny

- H₀ nie odrzucamy

- H₀ odrzucamy

Brak autokorelacji

Autokorelacja składników losowych modelu.

Jedno z klasycznych założeń MNK dotyczyło kowariancji składników losowych odległych od siebie o s- jednostek czasu

Jeżeli założenie to nie jest spełnione tzn, gdy zachodzi nierówność

to składniki losowe są skorelowane , występuje autokorelacja składników losowych odległych od siebie o s- jednostek czasu (jeżeli s=1 zachodzi autokorelacja rzędu pierwszego).

Jeśli jest to zależność liniowa to mamy następujący model

gdzie: p - współczynnik autokorelacji rzędu pierwszego spełniający nierówność

-1

Przyczyny autokorelacji:

1. Błędy w budowie modelu ekonometrycznego

• pominięcie istotnych zmiennych objaśniających

• niewłaściwa postać analityczna modelu

• wprowadzenie zmiennych o niewłaściwych opóźnieniach

2. Okres przyjęty za jednostkę jest krótszy od czasów działania czynników przypadkowych tzw. autokorelacja czysta

Test DURBINA WATSONA

H₀ : p₁ = 0 (p - ro)

H₁ : p₁ > 0

,

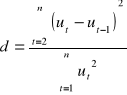
jeżeli: r₁ = 0 to d = 2

r₁= 1 to d = 0

r₁ = -1 to d = 4

Dla ustalonego n, k-1, α i n>15 z tablic odczytujemy d₁ i d_u (interesuje nas liczba zmiennych a nie liczba parametrów).

Gdy:

1. d > d_u - H₀ przyjmujemy

2. d < d₁ - H₀ odrzucamy

3. d₂
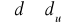
   test nie daje odpowiedzi

4. r₁< 0 , obliczamy d^* = 4 - d

Gdy H₀ jest prawdziwa to E(d) = 2

Jeżeli d
to prawdopodobnie p₁
(czyli autokorelacja nie istnieje)

Test jednorodności wariancji GOLDFELDA QUANDTA

Czynności:

• podział próby na dwie równe części

• opuszczamy około 4 do 8 środkowych elementów

• szacujemy parametry modeli
  
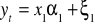
  i
  
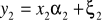
  w obu próbach

• obliczamy wariancje resztowe dla obu modeli, czyli
  i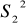
  

Test:

H₀ :

H₁ :

Jeżeli H₀ jest prawdziwa to:

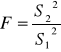
ma rozkład Fischera Snedecora o m₁ = (n₂ - k) i m₂ = (n₁ - k) stopniach swobody.

Jeżeli przy poziomie istotności

F > F_α

to hipotezę o jednorodności wariancji należy odrzucić.

Test moralności rozkładu składnika losowego JARQUE BERA

H₀ : składnik losowy ma rozkład normalny

H₁ : składnik losowy modelu nie ma rozkładu normalnego

Statystyka testu

gdzie:

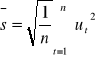
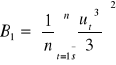
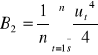
Dowodzi się, że statystyczna JB ma rozkład χ² (chi) z dwoma stopniami swobody.

Dla α = 0,05 wartość krytyczna testu wynosi 5,991, czyli gdy JB > 5,991to H₀ o normalnym rozkładzie należy odrzucić

Test serii (ciąg dalszy przykładu ze str. 12)

t	yt	y*t	ut	X1t^2
1	35,0	34,8	0,2	A (1)
2	35,2	35,4	-0,2	B (2)
3	35,7	35,6	0,1	A (3)
4	35,0	35,2	-0,2	B (4)
5	36,4	36,4	0
6	36,5	36,4	0,1	A (5)
7	36,4	36,4	0
8	37,1	37,4	-0,3	B (6)
9	37,6	37,4	0,2	A (7)
10	37,1	37	0,1	A (7)
Σ	362	362	0,0

H₀ : reszty są losowe

H₁ : reszty nie są losowe

Empiryczna ilość serii - C = 7

n₁ = 5 reszty dodatnie

n₂ = 3 reszty ujemne n₁ - n₂ = 5 - 3 = 2

dla α = 0,5 C_α = 2 taka, że P{C< C_α}=α

C > C_α nie ma podstaw do odrzucenia H₀

Test serii

H₀ :

H₁ :

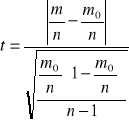
m- reszty dodatnie = 5 , n - ogólna liczba reszt = 8

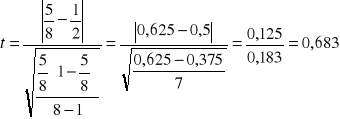
α = 0,05 ; n - 1 = 7 ; t_α = 2,365

< t_α - nie ma podstaw do odrzucenia H₀

Analiza reszt - test Durbina Watsona

t	yt	y*t	ut	ut-1	ut - ut-2	(ut - ut-2)^2	ut^2
1	35,0	34,8	0,2	-	-	-	0,04
2	35,2	35,4	-0,2	0,2	-0,4	0,16	0,04
3	35,7	35,6	0,1	-0,2	0,3	0,09	0,01
4	35,0	35,2	-0,2	0,1	-0,3	0,09	0,04
5	36,4	36,4	0	-0,2	0,2	0,04	0
6	36,5	36,4	0,1	0	0,1	0,01	0,01
7	36,4	36,4	0	0,1	-0,1	0,01	0
8	37,1	37,4	-0,3	0	-0,3	0,09	0,09
9	37,6	37,4	0,2	-0,3	0,5	0,25	0,04
10	37,1	37	0,1	0,2	-0,1	0,01	0,01
Σ	362	362	0,0			0,75	0,28

H₀ : p₁ = 0 reszty przepisujemy z poprzedniej kolumny (odległe od siebie o 1)

H₁ : p₁ > 0

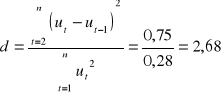
d^* = 4 - d = 4 - 2,68 = 1,32

dla n =10 , k -1 = 2, α= 0,05 d_l = 0,697 , d_u = 1,641 0,697 < d^* < 1641

Test nie daje jednoznacznej odpowiedzi.

Własności składników losowych

Sferyczność składników losowych

Jeżeli klasyczne założenia MNK w stosunku do składników losowych są spełnione, czyli gdy:

• nie występuje autokorelacja,

• wariancje są stałe, jednorodne,

to macierz wariancji i kowariancji składowych losowych dana jest wzorem:

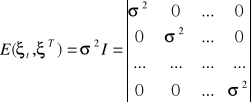
wtedy składniki losowe są sferyczne

Niesferyczność składników losowych

Pierwsza forma niesferyczności to autokorelacja.

Druga forma niesferyczności to niejednorodność wariancji.

W warunkach niesferyczności nie można stosować MNK ponieważ estymatory obciążone są dużymi błędami.

Metoda Cochrane'a Orcutt'a

Transformacja zmiennych.

y_t* = y_t -ρy_t-1

(ρ z próby w przykładzie = - 0,48)

x_it* = x_it - ρx_it-1 i = 1, 2, ..... k

gdy x_ut = 1 to x_ut* = 1 - ρ (w praktyce ρ = r)

Powrót do modelu pierwotnego

a_i* = a_i

a₀* = a₀(1 - r )

gdy
, stosujemy metodę różniczki zupełnej

- wzór na wyraz wolny

Analiza szeregów czasowych - budowa modeli tendencji rozwojowych

Modele tendencji rozwojowych budowane są na podstawie szeregów czasowych.

Szereg czasowy to zbiór uporządkowanych w czasie realizacji zmiennych.

Części składowe szeregów czasowych Y_t:

• składowa systematyczna f(t) - to efekt oddziaływania na zmienną stałego zestawu czynników zwanych przyczynami głównymi

• składowa przypadkowa ξ_t - to składnik losowy, wahania przypadkowe

Y_t ={ f(t) ; ξ_t }

Formy składowej systematycznej:

• trend - tendencja rozwojowa, długookresowa skłonność do jednokierunkowych zmian (wzrost lub spadek)wartości zmiennej prognozowanej , opisowej

• przeciętny stały poziom zjawiska dodanego - występuje wtedy gdy w szeregu czasowym nie występuje tendencja rozwojowa.

Wahania regularne - wahania wokół trendu lub stałego przeciętnego poziomu zmiennej powtarzające się w tych samych okresach ze stałym bądź zmiennym nasileniem, są wśród nich:

• wahania cykliczne - długookresowe rytmiczne wahania wartości Y_t wokół trendu lub stałego przeciętnego poziomu, powtarzające się w okresach dłuższych niż rok, związane z cyklami koniunkturalnymi gospodarki.

• wahania sezonowe - wahania wartości Y_t wokół trendu lub stałego przeciętnego poziomu powtarzające się w obrębie roku , wynikające z np. występowania pór roku, zwyczajów ludności itp.

• wahania krótkookresowe - powtarzające się w okresach krótszych niż rok, np. w kwartałach, miesiącach, tygodniach, dniach ....

Modele trendu

• 
  
  
  
  
  
  
  
  
  
  
  Model addytywny - zaobserwowane wartości zmiennej Y_t są sumą wszystkich bądź tylko niektórych składowych szeregu czasowego
  
  Y
  
  
  
  
  
  
  
  
  

• t

Y = T + W + P

• Model multiplikatywny - zaobserwowane wartości zmiennej Y_t są iloczynem wszystkich bądź tylko niektórych składowych szeregu czasowego

















Y

Y =T * W * P

Każdą analizę szeregu czasowego należy rozpocząć od wykonania wykresu na podstawie którego ustalamy czy trend można przedstawić za pomocą funkcji zmiennej czasowej t.

Metody używane do wyznaczenia funkcji trendu.

1. Metoda analityczna - polega na tym, że w oparciu o wstępny wykres ustalamy konkretną postać analityczną trendu i na podstawie danych statystycznych szacujemy postać tej funkcji.
   
   Typowe postacie funkcji trendu:


- funkcja liniowa


- funkcja logarytmiczna






- funkcja wykładnicza





- funkcja hiperboliczna


- funkcja potęgowa


- trend logistyczny

2. Metoda mechaniczna - oblicza się średnie ruchome. Wygładzanie szeregu czasowego polega na przyporządkowaniu kolejnym realizacjom szeregu empirycznego wartości średnich obliczonych sekwencyjnie na podstawie np. k<n obserwacji. Obliczona średnia przypada na środkowy okres biorący udział w liczeniu.

Załóżmy, że dane są wartości zmiennej y₁, y₂, y₃, .... y_n i niech k=3, wtedy średnie ruchome obliczane są następująco:










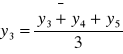
k = 3

yt	y^*t
y1 y2 y3 y4 .. .. yn	- y1 y2 y3 .. .. -

Jeżeli k jest liczbą parzystą np. równą 4, wtedy średnie ruchome obliczane są w drodze tzw. centrowania , czyli





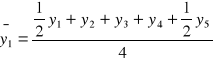
itd.

Liczba elementów na podstawie których oblicza się kolejne średnie czyli k najczęściej równa jest ilości okresów w całym cyklu wahań.

k=4

yt	y^*t
y1 y2 y3 y4 yn-1 yn	- - y1 y2 - -

Wyznaczanie wahań periodycznych (regularnych wahań)

Gdy chcemy zbadać jakość zjawiska wykorzystujemy zmienne 0, 1 (zerojedynkowe)

V_i - i = 1, 2, ....... m - liczba faz w cyklu wahań

Vi	1 dla i-tej fazy wahań 0 dla pozostałych m-1 faz wahań

Załóżmy, że m = 4 (kwartały)

	V1	V2	V3	V4
I II III IV	1 0 0 0	0 1 0 0	0 0 1 0	0 0 0 1
I II III IV	1 0 0 0	0 1 0 0	0 0 1 0	0 0 0 1

Model Klein'a pozwala opisać cały model


każda zmienna ma swój parametr (wyraz wolny - jedynki)

f(t) - funkcja trendu


- stałe parametry i = 1, 2, ...... m

V_it - zmienne zerojedynkowe

Ponieważ:




suma parametrów = 0, to możemy pominąć jeden parametr a brakujący szacujemy ze wzoru


(nie szacujemy ostatniego parametru)




Wtedy model jest następujący:




czyli




Metoda wskaźnikowa wyznaczania efektów periodycznych

Parametry mierzy się w jaki sposób odchyla się realizowana zmienna Y od poziomu wyznaczonego przez trend w wyniku obserwacji i-tej fazy wahań.

Metoda wskaźnikowa wyznaczania efektów periodycznych przeprowadzana jest w 4 etapach.

1. Wyodrębnienie tendencji rozwojowej, wygładzenie szeregu

• metoda analityczna

• metoda mechaniczna

obliczamy wartość teoretyczną y^*_ti

2. Eliminacja tendencji rozwojowej (wyrzucamy t z szeregu)

model addytywny model multiplikatywny





3. Z tego co zostało wyrzucamy efekty przypadkowe (eliminacja wahań periodycznych)
   Surowe wskaźniki periodyczne , jest ich tyle ile jest faz cyklów wahań.




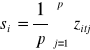
gdzie:

s_i - wskaźnik surowy dla okresu i

j - 1, 2, ... p , kolejny numer cyklu w badanym szeregu

p - liczba jednoimiennych faz w szeregu (grupy faz)

4. Korygowanie wskaźników surowych, obliczanie wskaźników czystych

Jeśli
w modelu addytywnym lub
w modelu multiplikatywnym, to obliczamy średnią wartość wskaźników i korygujemy nią wskaźniki surowe.








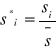
model addytywny model multiplikatywny

Interpretacja wskaźników :

1. s^*_j w modelu multiplikatywnym - informuje o ile procent poziom zjawiska w danej i-tej fazie wahań jest niższy lub wyższy od poziomu jaki osiągnęłoby zjawisko gdyby jego rozwój następował zgodnie z tendencją rozwojową

2. s^*_j w modelu addytywnym - informuje o ile jednostek poziom zjawiska w danej i-tej fazie wahań jest niższy lub wyższy od poziomu jaki osiągnęłoby zjawisko gdyby jego rozwój następował zgodnie z tendencją rozwojową

Przykład z materiałów „ sprzedaż konserw warzywnych w poszczególnych kwartałach”

Prognozowanie zmiennej endogenicznej w przyszłości

Predykcja ekonometryczna - ogół zasad i metod prognozowania w przyszłości na podstawie odpowiedniego modelu ekonometrycznego. Celem tego procesu jest prognoza.

Prognoza ekonometryczna y_Tp - wynik procesu predykcji przy przyjętych z góry założeniach.




i = 1, 2, ...... k

a_i - oszacowanie i-tego parametru strukturalnego modelu

x_it - wartość i-tej zmiennej objaśniającej modelu w okresie prognozowym T

Podstawowe założenia predykcji ekonometrycznej prognozowania w przyszłości

1. Znany jest model ekonometryczny wyjaśniający kształtowanie się zmiennej dla , której należy zbudować prognozę.

2. Struktura opisywanych przez model zjawisk jest stabilna w czasie tzn., że model jest aktualny również w okresie prognozowanym „T”.

3. Rozkład składnika losowego nie ulega zmianom w czasie.

4. Znane są dla okresu prognozowanego „T” wartości zmiennych objaśniających występujących w modelu będącym podstawą predykcji.

5. Dopuszczalna jest ekstrapolacja modelu poza zaobserwowany w próbie obszar zmienności zmiennych objaśniających.

Zasada predykcji nieobciążonej





Zasada predykcji wg największego prawdopodobieństwa




Mierzenie dokładności prognoz

Mierniki EX ANTE - charakterystyki lub prawdopodobieństwa, które są obliczane na podstawie znajomości rozkładu zmiennej prognozowanej błędów predykcji. Miary te informują już w momencie budowania prognozy, jaki będzie rząd dokładności przewidywania.

Mierniki EX POST - charakterystyki rozkładu błędów predykcji lub częstości względne realizacji trafnych prognoz zaobserwowane w wyniku porównywania prognoz z odpowiadającymi im realizacjami zmiennej prognozowanej.

Realizacja błędów prognoz.

U_T = y_T - y_Tp

y_T - realizacja zmiennej y_T w czasie T

y_Tp - prognoza dla okresu T

Wariancja predykcji

Podstawowy miernik ex ante w warunkach predykcji nieobciążonej i powtarzalnej, opartej na modelu liniowym oszacowanym MNK




gdzie:


- transponowany wektor założonych dla okresu prognozowanego T wartości zmiennych

objaśniających


- macierz wariancji i kowariancji estymatorów


- wariancja resztowa


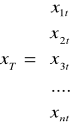
- wektor kolumnowy

V² - wariancja

Wariancja predykcji :

• mierzy rząd dokładności predykcji przy założeniu, że przyjęte przy obliczaniu prognozy wartości zmiennych objaśniających faktycznie się realizują

• zależy od wielkości próby

• jest nie mniejsza od wariancji składnika losowego

Średni błąd predykcji




Błąd średni predykcji informuje o ile średnio rzecz biorąc w długim ciągu predykcji rzeczywiste realizacje y_T będą się odchylać (in plus i in minus) od wartości obliczonej prognozy.

Średni względny błąd predykcji




Wyraża stosunek średniego błędu predykcji do jej wartości.

Okres empirycznej weryfikacji prognoz I_ep - to m elementarny odcinek czasowy w przeszłości z którego pochodzą dane dotyczące prognoz i realizacji zmiennej wykorzystywane do obliczania wartości mierników ex post.

Miary ex post

Średni błąd prognozy




m - długość okresu empirycznej weryfikacji prognoz, liczba okresów prognozowanych

y_T - realizacja zmiennej y_T w okresie T

y_Tp - prognoza dla okresu T

Empiryczna wariancja predykcji





- MSE

s_p - średni empiryczny błąd prognozy = RMSE




Średni absolutny błąd prognozy







Przykład:

Dany jest model:

Y_t = 19,338 X_1t + 724,331 X_2t - 26996,73 + u_t

Gdzie:

Y_t - samochody osobowe zarejestrowane tys. szt. (stan w dniu 31 XII)

X_1t - drogi publiczne o twardej nawierzchni w tys. km. (stan w dniu 31 XII)

X_2t - liczba ludności w kraju w mln. Osób (stan w dniu 31 XII)

T = 1976, 1977, ...., 1990.

Prognoza na rok 1991, przy założeniu, że X_1T = 225,7 tys. km , X_2T = 38,3 mln. osób

Y_{tP =} 19,338* 225,7 + 724,331* 38,3 -26996,73 = 5109,734 tys. szt.

Prognoza na rok 1992, przy założeniu, że X_1T = 229,1 tys. km , X_2T = 38,4 mln. osób

Y_{tP =} 19,338* 229,1 + 724,331* 38,4 -26996,73 = 5247,916 tys. szt.

Wariancja predykcji, średni względny błąd predykcji (na rok 1991)

Wiemy ponadto, że:


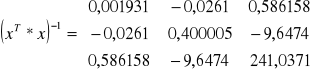
, s² = 27340,97





+

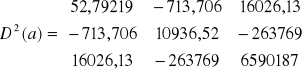
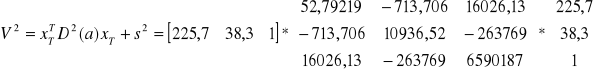
+ 27340,97 = 39934,32





Ekonometria menedżerska

24

Tutaj musi być najmniej (minimalnie)

Składnik losowy

reszta

Wartość teoretyczna













Całkowita

zmienność y_t

Zmienność objaśniona zmiennej y_t

Zmienność resztowa u_t

błąd

Moduł- wartość bezwzględna

y*_t =2x_n + 0,4x_2t + 29,4

y*₁ =2* 0,7 + 0,4*10 +29,4 = 34,8

y*₂ = 2*0,8 + 0,4*11 + 29,4 = 35,4

u_t = y_t - y*_t

u₁ = 35 -34,8 = 0,2

u₂ = 35,2 -35,4 = -0,2

( empiryczna ilość serii)

A - reszty dodatnie

B - reszty ujemne

Reszty zerowe pomijamy

trend

Odchylenia od trendu o stałej amplitudzie

0

t

trend

Amplitudy wahań wokół trendu są coraz większe lub mniejsze

Szereg teoretycznych wartości jest o 4 elementy krótszy

	V1-V3 V^*1t	V2-V3 V^*2t
I II III	1 0 -1	0 1 -1
I II III	1 0 -1	0 1 -1

---