ZASTOSOWANIE LINIOWYCH PROBLEMÓW DECYZYJNYCH W KIEROWANIU EKSPLOATACJĄ
W programowaniu liniowym poszukuje się odpowiedzi na następujące pytania:
- jak rozdzielić zasoby rozmieszczone w kilku punktach do kilku odbiorców aby koszt (lub czas) transportu był najmniejszy?
- jak zaplanować wykorzystanie wielu maszyn przy obróbce wielu produktów aby wydajność systemu eksploatacji była największa?
- jak zorganizować cykl kontrolny działania systemu eksploatacji przy najniższych nakładach osobowych i materiałowych?
- itp.
Pozwala więc ono na wybór optymalnego systemu eksploatacji spośród wielu możliwych wariantów.
Przykład: punkt serwisowy wykonuje obsługę dwóch typów maszyn: X i Y. Zużycie materiałów eksploatacyjnych a i b przy obsłudze jednego egzemplarza maszyn jest określone. Znane i ograniczone są posiadane zapasy A i B tych materiałów. Znany jest zysk punktu serwisowego za wykonanie obsługi jednej maszyny cX i cY. Należy określić liczby maszyn poszczególnych typów, które punkt serwisowy powinien obsłużyć, aby uzyskać maksymalny dochód.
Tak sformułowany problem opiszemy za pomocą matematycznego modelu decyzyjnego wskazując przedtem jego elementy:
D - dziedzina modelu - maszyny typu X i Y, materiały eksploatacyjne a i b, zyski z obsługi cX i cY
R - relacje modelu - wielkości zużycia materiałów eksploatacyjnych aX i bX oraz aY i bY i zysku za dokonaną obsługę cX i cY
Z - założenia (ograniczenia) modelu - posiadane wielkości zapasów A i B materiałów eksploatacyjnych
F - kryterium modelu - maksymalizacja zysku
P - problem decyzyjny - liczby x i y obsłużonych maszyn typu X i Y.
Wielkościami niewiadomymi w przedstawionym problemie są liczby x i y maszyn typu X i Y. W problemach decyzyjnych nieznane wielkości, których wartość należy wyznaczyć w wyniku rozwiązania problemu, nazywamy zmiennymi decyzyjnymi. Tworzą one wektor zmiennych decyzyjnych. Jeżeli punkt serwisowy wykona obsługę x maszyn typu X i y maszyn typu Y to jej zysk możemy wyrazić (powinien on uzyskać wartość maksymalną) jako Z = cX x + cY y → max
Odpowiednio dopuszczalne zużycia materiałów eksploatacyjnych (ograniczenia) wyrażają nierówności:
aX x + aY y ≤ A
bX x + bY y ≤ B
Ze względu na charakter rozważanego problemu zmienne decyzyjne powinny przyjmować wartości nieujemne (x, y ≥ 0) i całkowite. Zauważmy, że w przedstawionym problemie decyzyjnym funkcja kryterium Z → max oraz wszystkie ograniczenia są funkcjami liniowymi (zmienne decyzyjne występują w pierwszej potędze).
Problem decyzyjny, w którym funkcja kryterium (celu) i ograniczenia są funkcjami liniowymi nazywamy liniowym problemem decyzyjnym lub zagadnieniem programowania liniowego.
Liniowe problemy decyzyjne są najczęściej występującymi problemami w praktyce kierowania eksploatacją maszyn.
Istnieje wiele algorytmów rozwiązywania zagadnień programowania liniowego dla różnych problemów decyzyjnych, jednak najczęściej stosuje się:
- metodę graficzną
- metodę „simplex”
- metodę transportową
Sformułowanie liniowego problemu decyzyjnego
Znaleźć wektor n zmiennych decyzyjnych X = [x1, x2,..., xn], który optymalizuje (maksymalizuje, minimalizuje) funkcję kryterium (celu) dla zadanych wag ci:
Z = c1 x1 + c2 x2 + ... + cn xn → max (min)
przy danych m ograniczeniach:
a11 x1 + a12 x2 + ... + a1n xn ≤ b1 ( ≥ b1)
a21 x1 + a22 x2 + ... + a2n xn ≤ b2
...
am1 x1 + am2 x2 + ...+ amn xn ≤ bm
oraz n warunkach brzegowych:
x1, x2,..., xn ≥ 0
gdzie współczynniki: aij, bi, cj są stałe i znane.
Zauważmy, że wektor zmiennych decyzyjnych X jest wektorem w przestrzeni n-wymiarowej, zaś liczba sformułowanych ograniczeń jest równa m.
Zazwyczaj, gdy poszukiwane jest maksimum funkcji celu, ograniczenia mają postać nierówności typu (≤), zaś gdy znajdujemy minimum funkcji celu, ograniczenia są nierównościami typu (≥). Powyższe sformułowanie problemu jest nazywane sformułowaniem algebraicznym ze względu na formę zapisu.
Problem może być sformułowany w postaci macierzowej: znaleźć wektor zmiennych decyzyjnych X, który optymalizuje formę liniową (ograniczymy się do zapisu maksimum funkcji celu): Z = CX → max przy danych ograniczeniach: A X ≤ B i X ≥ 0 gdzie:
X - wektor zmiennych decyzyjnych;
C - wektor wag (współczynników wagowych);
A - macierz współczynników ograniczeń;
B - wektor ograniczeń:
C = [c1, c2, ..., cn]; 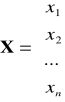
; 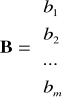
; 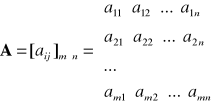
Liniowy problem decyzyjny można zapisać także w postaci wektorowej: znaleźć wektor zmiennych decyzyjnych X, który optymalizuje formę liniową: Z = C X → max przy danych ograniczeniach:
A1 x1 + A2 x2 + ... + Aj xj + ... + An xn ≤ B gdzie: C = [c1, c2, ..., cn]; 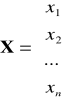
; 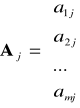
; 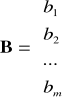
Własności rozwiązania zagadnienia programowania liniowego
Rozwiązaniem dopuszczalnym zagadnienia programowania liniowego nazywamy każdy wektor zmiennych decyzyjnych X, który spełnia zbiór ograniczeń liniowego modelu decyzyjnego.
Rozwiązaniem bazowym liniowego problemu decyzyjnego nazywamy takie rozwiązanie dopuszczalne X, którego nie więcej niż m składowych jest większych od zera, a pozostałe równe zero.
Na przykład: X = [x1, x2, ...,xk, 0, 0, ... , 0], gdzie k ≤ m.
Rozwiązaniem bazowym niezdegenerowanym zagadnienia programowania liniowego nazywamy takie rozwiązanie dopuszczalne X, w którym dokładnie m składowych jest większych od zera, a pozostałe równe zero.
Na przykład: X = [x1, x2, ...,xm, 0, 0, ... , 0].
Zbiór wszystkich rozwiązań dopuszczalnych zagadnienia programowania liniowego jest zbiorem wypukłym.
Ilustracja zbioru wypukłego na płaszczyźnie.
Twierdzenie Weierstrassa: Liniowa funkcja celu Z = CX przyjmuje wartość optymalną (maksymalną, minimalną) w punkcie wierzchołkowym zbioru rozwiązań dopuszczalnych zagadnienia programowania liniowego. Jeśli przyjmuje wartość optymalną więcej niż w jednym punkcie wierzchołkowym, to przyjmuje tę samą wartość dla każdej kombinacji liniowej tych punktów (graficznie dla wszystkich punktów odcinka łączącego te punktu wierzchołkowe).
Przedstawione definicje i twierdzenia wskazują dwa charakterystyczne etapy rozwiązania liniowego problemu decyzyjnego:
określenie zbioru rozwiązań dopuszczalnych w oparciu o istniejące ograniczenia problemu decyzyjnego;
badanie wartości funkcji kryterium w punktach wierzchołkowych zbioru rozwiązań dopuszczalnych i wybór jako rozwiązania wartości wektora zmiennych decyzyjnych w tym punkcie, w którym funkcja osiąga wartość optymalną.
Metoda graficzna rozwiązywania zagadnienia programowania liniowego
Metoda graficzna służy do rozwiązywania zagadnień liniowych o co najwyżej trzech, a praktycznie dwóch zmiennych decyzyjnych. Wykorzystuje się tutaj możliwość przedstawienia problemu w postaci graficznej.
W przestrzeni dwuwymiarowej zagadnienie liniowe z kryterium maksymalizacji funkcji celu sprowadza się do następującej postaci:
- funkcja celu:
Z = c1 x1 + c2 x2 → max
- ograniczenia:
a11 x1 + a12 x2 ≤ b1
a21 x1 + a22 x2 ≤ b2
...
am1 x1 + am2 x2 ≤ bm
x1, x2 ≥ 0
Ograniczenia problemu decyzyjnego stanowią układ nierówności liniowych. Zatem wyznaczenie zbioru rozwiązań dopuszczalnych jest równoważne znalezieniu rozwiązania układu nierówności (graficznie obszaru płaskiego w układzie współrzędnych określonych przez zmienne decyzyjne x1 - x2 będącego częścią wspólną półpłaszczyzn będących rozwiązaniami nierówności liniowych ograniczeń problemu).
Maksimum funkcji celu w zbiorze rozwiązań dopuszczalnych znajdziemy wyznaczając jej gradient (gradient wskazuje kierunek najszybszego wzrostu funkcji): 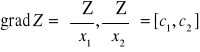
i zaczepiając go w początku układu współrzędnych. Zauważmy, że linia prostopadła do kierunku wektora gradientu jest linią ekwipotencjalną, tj. linią stałej wartości funkcji celu. Przesuwając tę linię równolegle w stronę zwrotu gradientu w zbiorze rozwiązań dopuszczalnych znajdujemy punkty, w których funkcja kryterium przyjmuje coraz wyższe wartości. Ostatni na kierunku gradientu punkt wspólny (punkty wspólne) linii ekwipotencjalnej i zbioru rozwiązań dopuszczalnych (jeden z punktów wierzchołkowych lub odcinek łączący punkty wierzchołkowe leżące na jednej prostej) jest punktem, którego współrzędne stanowią poszukiwane rozwiązanie - współrzędne wektora zmiennych decyzyjnych.
Algorytm graficznej metody rozwiązania zagadnienia programowania liniowego jest następujący:
1. Ograniczenia sprowadza się do postaci odcinkowej równań prostych (zachowując znaki nierówności) poprzez podzielenie odpowiednio nierówności obustronnie przez bi.
Stosując podstawienie 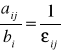
otrzymuje się nowy układ nierówności ograniczeń 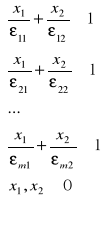
, gdzie 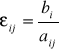
oznaczają bezpośrednio współrzędne punktów przecięcia kolejnych prostych i z osiami układu współrzędnych xj (jest to postać równania prostej najbardziej dogodna do wykreślania wykresu funkcji liniowej).
2. W układzie współrzędnych xj wykreśla się zbiór rozwiązań dopuszczalnych jako zbiór rozwiązań powyższego układu nierówności (jako część wspólną półpłaszczyzn będących rozwiązaniami wszystkich nierówności ograniczeń).
Uwaga: układ współrzędnych powinien mieć osie liczbowe o wektorach jednostkowych takiej samej długości.
3. Znaleźć współrzędne wektora gradZ.
4. Wyznaczyć kierunek wektora gradZ na płaszczyźnie w obszarze zbioru rozwiązań dopuszczalnych, np. umieszczając punkt początkowy wektora w początku układu współrzędnych.
5. Wykreślić linię ekwipotencjalną prostopadłą do wektora gradZ przechodzącą przez punkt początkowy wektora.
6. Przesuwać linię ekwipotencjalną równolegle w stronę wzrostu funkcji Z (zgodnie ze zwrotem wektora gradZ) aż do przecięcia z ostatnim punktem wierzchołkowym zbioru rozwiązań dopuszczalnych - punkt ten wyznacza poszukiwane rozwiązanie optymalne X* = [x1*, x2*].
Jeżeli należy znaleźć minimum funkcji celu, linię ekwipotencjalną przesuwamy rozpoczynając od dowolnego punktu wewnętrznego zbioru rozwiązań dopuszczalnych w kierunku przeciwnym do zwrotu wektora gradZ.
Jeżeli dziedziną wektora zmiennych decyzyjnych jest zbiór liczb całkowitych dodatnich, a uzyskane rozwiązanie optymalne wyrażone jest liczbami wymiernymi, konieczne jest badanie wartości funkcji kryterium w punktach należących do obszaru rozwiązań dopuszczalnych o współrzędnych całkowitych znajdujących się w otoczeniu danego punktu wierzchołkowego w celu znalezienia rozwiązania optymalnego spełniającego takie założenie.
Ilustracja rozwiązania zagadnienia programowania liniowego metodą graficzną.
Przykład
Rozwiązać metodą graficzną problem liniowy: Z = 6 x1 + 8 x2 → max
dla ograniczeń i warunków: 4 x1 + 6 x2 ≤ 360
8 x1 + 6 x2 ≤ 480
5 x1 + 4 x2 ≤ 400
x1, x2 ≥ 0
1. Ograniczenia sprowadzić do postaci odcinkowej równań prostych: ![]()
![]()
![]()
2. Wykreślić zbiór rozwiązań dopuszczalnych w układzie współrzędnych.
3. Obliczyć współrzędne wektora gradZ: 4. Wyznaczyć kierunek i zwrot wektora gradZ z początku układu współrzędnych. 5. Wykreślić linię ekwipotencjalną (prostopadłą) w punkcie początkowym wektora gradZ. 6. Przesunąć równolegle linię ekwipotencjalną w kierunku gradZ (poszukiwane jest |
|
maxZ) do ostatniego punktu wierzchołkowego zbioru rozwiązań dopuszczalnych. Współrzędne tego punktu wyznaczają rozwiązanie optymalne X* = [30, 40]
Otrzymane rozwiązanie oznacza, że dla uzyskania maksymalnej wartości funkcji celu w danych warunkach powinno sie przyjąć pierwszą zmienną decyzyjną równą 30 i drugą równą 40. Wówczas jej funkcja celu wyniesi Z = 6 x1 + 8 x2 = 6 ⋅ 30 + 8 ⋅ 40 = 500.
Metoda analityczna (SIMPLEX) rozwiązywania zagadnień programowania liniowego
Metoda Dantziga, lub inaczej metoda SIMPLEX, jest procedurą iteracyjną, co oznacza, że po wykonaniu pewnej liczby kroków możliwe jest uzyskanie rozwiązania optymalnego. Kolejne rozwiązania liniowego problemu decyzyjnego stanowią w tej metodzie współrzędne kolejnych punktów wierzchołkowych zbioru rozwiązań dopuszczalnych w n-wymiarowej przestrzeni (nie ma tu ograniczenia liczby zmiennych decyzyjnych). Zaczyna się od punktu wierzchołkowego zbioru rozwiązań, którego współrzędne są znane i mogą być użyte jako rozwiązanie początkowe - jest to punkt wierzchołkowy w początku układu współrzędnych, w którym wszystkie zmienne decyzyjne przyjmują wartości równe zero. Liczba iteracji (kolejnych sprawdzonych punktów wierzchołkowych) potrzebnych do znalezienia punktu optymalizującego jest szacowana na 3/2 do 3 m (liczby ograniczeń)
Algorytm omawianej metody został opracowany dla poszukiwania minimum liniowej funkcji celu. Dlatego w przypadku określenia maksimum liniowej funkcji celu należy skorzystać z zależności zmieniającej znak funkcji celu: maxZ = -min(-Z)
Algorytm metody SIMPLEX rozwiązania zagadnienia programowania liniowego jest następujący:
1. Przekształcić problem do postaci kanonicznej:
a) wprowadzić do modelu m nowych zmiennych decyzyjnych tzw. swobodnych lub funkcyjnych xn+1, xn+2, ... , xn+m
b) w nowej funkcji celu Z = c1 x1 + c2 x2 + ... + cn xn + cn+1 xn+1 + cn+2 xn+2 + ... + cn+m xn+m → min przyjąć odpowiednie wartości współczynników wagowych
c) w zbiorze ograniczeń wprowadzić macierz jednostkową Imxm dla zmiennych decyzyjnych swobodnych, a układ nierówności zamienić na układ równań
d) jeżeli poszukiwane jest maksimum funkcji celu to funkcję celu należy przekształcić według zależności maxZ = -min(-Z) oraz przyjąć zerowe współczynniki wagowe dla zmiennych swobodnych (dzięki temu funkcja celu dla pierwszej iteracji jest zerowa i dla kolejnych iteracji, po eliminacji kolejnych zmiennych swobodnych, rośnie)
e) jeżeli poszukiwane jest od razu minimum funkcji celu to współczynniki wagowe dla zmiennych swobodnych przyjmuje się bardzo duże (dzięki temu funkcja celu dla pierwszej iteracji jest ogromna i dla kolejnych iteracji, po eliminacji kolejnych zmiennych swobodnych, maleje)
W wyniku powyższych przekształceń problem decyzyjny poszukiwania maksimum funkcji celu przyjmuje następującą postać zapisu:
- funkcja celu:
-Z = - c1x1 - c2x2 - ... - cnxn - 0 xn+1 - 0 xn+2 - ... - 0 xn+m → min
- ograniczenia:
a11 x1 + a12 x2 +... + a1n xn + 1 xn+1 + 0 xn+2 + ... + 0 xn+m = b1
a21 x1 + a22 x2 + ...+ a2n xn + 0 xn+1 + 1 xn+2 + ... + 0 xn+m = b2
...
am1 x1 + am2 x2 + ... + amnxn + 0 xn+1 + 0 xn+2 + ... + 1 xn+m = bm
x1, x2, ..., xn, xn+1, xn+2, ... , xn+m ≥ 0
2. Warunki zadania przedstawia się w postaci tablicy liczbowej
|
|
cj |
-c1 |
-c2 |
... |
-cn |
0 |
0 |
... |
0 |
|
Br |
Aj ci |
A1 |
A2 |
... |
An |
An+1 |
An+2 |
... |
An+m |
b1 |
An+1 |
0 |
a11 |
a12 |
... |
a1n |
1 |
0 |
... |
0 |
b2 |
An+2 |
0 |
a21 |
a22 |
... |
a2n |
0 |
1 |
... |
0 |
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
... |
bm |
An+m |
0 |
am1 |
am2 |
... |
amn |
0 |
0 |
... |
1 |
|
-Zr zj-cj |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
|
gdzie
- w wierszu pierwszym (zaczynając od kolumny trzeciej) znajdują się współczynniki funkcji celu (kolor zielony)
- w wierszu drugim (zaczynając od kolumny trzeciej) znajdują się oznaczenia wektorów ograniczeń Aj, a poniżej ich współrzędne (elementy macierzy współczynników) (kolor niebieski)
- w kolumnie drugiej (oprócz ostatniego wiersza) znajdują się nazwy wektorów tworzących bazę Br rozwiązań dopuszczalnych dla r-tej iteracji (rozwiązania). Jeżeli w bazie tej nie ma jakiegoś wektora Ai≠j to przyjmuje się że zmienna decyzyjna o tym samym numerze i jest równa zeru. Dla pierwszej iteracji są nimi wektory jednostkowe Aj, odpowiadające zmiennym decyzyjnym swobodnym, wpisane w takiej kolejności, aby w klatce będącej częścią wspólną wiersza i kolumny, w której są wpisane oznaczenia wektora Aj znajdowała się współrzędna 1, a pozostałe były równe 0 (kolor ciemnoniebieski)
- w kolumnie trzeciej (oprócz ostatniego wiersza) znajdują się współczynniki ci funkcji celu odpowiadające wektorom bazy wpisanym w kolumnie drugiej. Dla pierwszej iteracji wszystkie ci = 0 (kolor ciemnozielony)
- w kolumnie pierwszej (oprócz ostatniego wiersza) znajdują się wartości niezerowych współrzędnych wektora zmiennych decyzyjnych Xr dla r-tej iteracji. Dla pierwszej iteracji są nimi wartości zmiennych swobodnych równe wartościom kolejnych ograniczeń xn+1 = b1, xn+2 = b2, ... ,xn+m = bm, czyli w rozwiązaniu wyjściowym rzeczywiste zmienne decyzyjne mają wartości równe zero (kolor czerwony).
- w ostatnim wierszu tabeli w kolumnie drugiej i trzeciej znajdują się oznaczenia funkcji celu dla r-tej iteracji (pomarańczowy) i wielkości zj - cj dla tej iteracji (brązowy).
Przyjmuje się następujące oznaczenia:
i - numer wiersza (oprócz wiersza pierwszego, drugiego i ostatniego) zgodny z indeksem wektora bazy;
j - numer kolumny (oprócz kolumny pierwszej, drugiej i trzeciej) zgodny z indeksem wektora bazy
xi - element kolumny pierwszej - współrzędna wektora zmiennych decyzyjnych Xr uzyskanego dla r-tej iteracji (te współrzędne wektora Xr, które nie znajdują się w tabeli dla r-tej iteracji są równe zero)
aij - elementy tablicy odpowiadające elementom macierzy współczynników
3. Obliczyć wartość funkcji celu: ![]()
i wstawić do ostatniego wiersza pierwszej kolumny (pomarańczowy). Jest to suma iloczynów elementów kolumny trzeciej ci (ciemnozielonej) i współrzędnych wektora zmiennych decyzyjnych Xr (kolumny pierwszej - czerwonej). Dla pierwszej iteracji wartość funkcji celu jest równa 0, ponieważ wszystkie ci = 0
4. Obliczyć elementy zj - cj ostatniego wiersza tabeli: ![]()
gdzie zj jest iloczynem ci (ciemnozielony) i odpowiedniego wektora kolumnowego Aj = [aij] a cj (zielony) odpowiada wektorowi Aj i wstawić do ostatniego wiersza kolumn j (brązowy)
Uwaga: Dla pierwszej iteracji wartości zj - cj są przeciwne do wartości współczynników funkcji ceku cj w wierszu pierwszym bo zj dla tej iteracji jest zerem (bo wszystkie ci = 0). W każdym kroku iteracji wartości zj - cj są równe zero w kolumnach wektorów Aj znajdujących się w aktualnej bazie rozwiązania, czyli wektorów będących jednocześnie wektorami Ai (wykorzystanie tych faktów znacznie zmniejsza pracochłonność stosowania metody)
5. Sprawdzić, czy w ostatnim wierszu tabeli istnieją zj - cj > 0 dla wektorów Aj spoza bazy (dla wektorów bazy zj - cj = 0):
a) jeśli nie istnieją (wszystkie zj - cj ≤ 0), to otrzymane rozwiązanie jest optymalne, przy czym niezerowe wartości wektora zmiennych decyzyjnych X znajdują się w kolumnie pierwszej tabeli (czerwony), a wartość funkcji celu (-Z) w lewym dolnym rogu tabeli (pomarańczowy). Oznacza to zakończenie rozwiązywania problemu decyzyjnego;
b) jeśli istnieją zj - cj > 0, to rozwiązanie należy kontynuować (pkt 6 algorytmu);
c) jeśli nie istnieją zj - cj > 0, ale istnieją zj - cj = 0 dla wektorów spoza bazy, to problem ma także inne rozwiązanie o tej samej wartości funkcji celu (w innym punkcie wierzchołkowym zbioru rozwiązań dopuszczalnych). Rozwiązanie należy kontynuować (pkt 6 algorytmu).
6. Znaleźć taki numer kolumny j = k, dla którego zachodzi: ![]()
Uwaga: dla przypadku 5c) kolumną o numerze k jest kolumna wektora Aj spoza bazy, w której zj - cj = 0.
7. Dla kolumny o numerze j = k obliczyć ilorazy: ![]()
dzieląc wartości wektora Xr (czerwone) przez współrzędne wektora Ak (niebieskie z kolumny o numerze k) a następnie wybrać numer wiersza i = l, dla którego zachodzi: 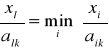
Uwaga: celowe i wygodne dla dalszej realizacji obliczeń jest oznaczenie, np. za pomocą strzałek, kolumny k i wiersza l oraz elementu tablicy alk (np. podwójną linią).
8. Zbudować nową tabelę w celu otrzymania kolejnego rozwiązania:
a) przepisać bez zmian elementy cj wiersza pierwszego (zielone) oraz oznaczenia wektorów Pj w wierszu drugim (niebieskie);
b) w bazie B (ciemnoniebieskie) w miejsce wektora Al wpisać wektor Ak a pozostałe wektory bazy przepisać bez zmian;
c) w kolumnie trzeciej (ciemnozielone) wpisać współczynniki wektora wag ci odpowiadające wektorom bazy;
d) pozostałe elementy tablicy obliczyć według wzorów (x'i oraz a'ij oznaczają elementy nowej tablicy):
- elementy Xr (czerwone) (pierwszej kolumny): 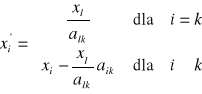
- elementy Pj (niebieskie) (kolejnych kolumn): 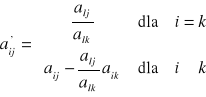
Uwaga: W nowej tablicy można wpisać bezpośrednio, bez konieczności wykonywania obliczeń, współrzędne wektorów jednostkowych Aj znajdujących się w aktualnej bazie B, gdyż aij = 1 dla i = k a pozostałe aij = 0.
9. Powrócić do punktu 3 algorytmu.
Uwagi:
- jeżeli istnieje zk - ck > 0, zaś wszystkie aik są mniejsze lub równe zero (pkt 7. algorytmu), to problem liniowy nie ma rozwiązania skończonego,
- zmiana wartości funkcji celu w każdym kolejnym kroku iteracji jest równa: ![]()
- algorytm metody można łatwo implementować na maszyny cyfrowe. Jednakże rozwiązanie za pomocą EMC ze względu na dużą liczbę działań arytmetycznych (w szczególności ilorazów) i zaokrągleń może być niekiedy obarczone błędem.
Przykład
Problem decyzyjny z poprzedniego przykładu rozwiązać metodą analityczną SIMPLEX.
Z = 6 x1 + 8 x2 → max
4 x1 + 6 x2 ≤ 360
8 x1 + 6 x2 ≤ 480
5 x1 + 4 x2 ≤ 400
x1, x2 ≥ 0
Zgodnie z podanym algorytmem należy:
1. Przekształcić problem do postaci kanonicznej - w wyniku tego otrzymujemy:
- Z = - 6 x1 - 8 x2 + 0 x3 + 0 x4 + 0 x5 → min
4 x1 + 6 x2 + 1 x3 + 0 x4 + 0 x5 = 360
8 x1 + 6 x2 + 0 x3 + 1 x4 + 0 x5 = 480
5 x1 + 4 x2 + 0 x3 + 0 x4 + 1 x5 = 400
x1, x2 ≥ 0 (również: x3, x4, x5 ≥ 0)
Do problemu wprowadzono trzy zmienne decyzyjne swobodne, ponieważ model matematyczny zawiera trzy ograniczenia.
2. Warunki zadania przedstawić w postaci tablicy
|
|
cj |
-6 |
-8 |
0 |
0 |
0 |
|
B1 |
Aj ci |
A1 |
A2 |
A3 |
A4 |
A5 |
360 |
A3 |
0 |
4 |
6 |
1 |
0 |
0 |
480 |
A4 |
0 |
8 |
6 |
0 |
1 |
0 |
400 |
A5 |
0 |
5 |
4 |
0 |
0 |
1 |
|
-Z1 zj-cj |
6 |
8 |
0 |
0 |
0 |
|
Wektor X1 zmiennych decyzyjnych ma współrzędne X1 = [x1, x2, x3, x4, x5] = [0, 0, 360, 480, 400]
3. Wartość funkcji celu: ![]()
(pomarańczowy)
4. Elementy zj - cj ostatniego wiersza tabeli (brązowy):
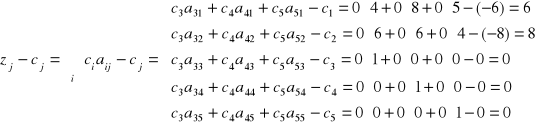
5. W ostatnim wierszu tabeli istnieją zj - cj > 0 dla wektorów Aj spoza bazy (dla wektorów bazy zj - cj = 0) i rozwiązanie X1 = [x1, x2, x3, x4, x5] = [0, 0, 360, 480, 400] nie jest optymalne
6. Numer kolumny j = k, dla którego zachodzi: ![]()
to j = k = 2
7. Dla kolumny o numerze j = k =2 ilorazy: 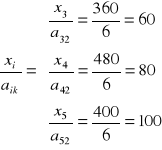
. Numer wiersza i = l, dla którego zachodzi: 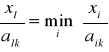
to i = l = 3
8. Nowa tabela w celu otrzymania kolejnego rozwiązania:
a) przepisane bez zmian elementy cj wiersza pierwszego (zielone) oraz oznaczenia wektorów Pj w wierszu drugim (niebieskie);
b) w bazie B (ciemnoniebieskie) w miejsce wektora A3 wpisany wektor A2 a pozostałe wektory bazy przepisane bez zmian;
c) w kolumnie trzeciej (ciemnozielone) wpisane współczynniki wektora wag ci odpowiadające wektorom bazy;
d) pozostałe elementy tablicy:
- elementy Xr (czerwone):
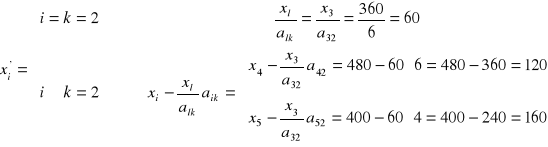
- elementy Pj (niebieskie):
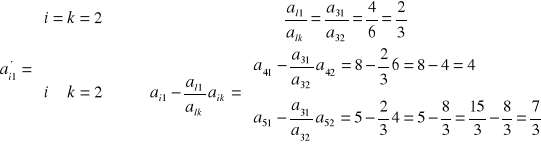
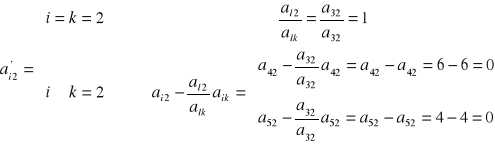
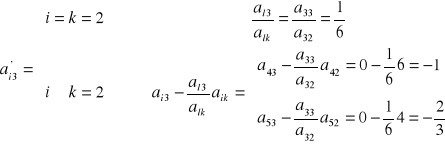
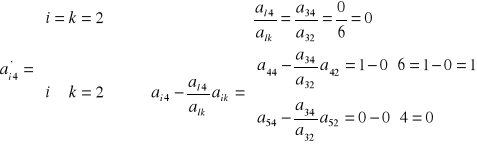
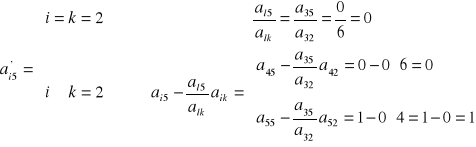
|
|
cj |
-6 |
-8 |
0 |
0 |
0 |
|
B2 |
Aj ci |
A1 |
A2 |
A3 |
A4 |
A5 |
60 |
A2 |
-8 |
2/3 |
1 |
1/6 |
0 |
0 |
120 |
A4 |
0 |
4 |
0 |
-1 |
1 |
0 |
160 |
A5 |
0 |
7/3 |
0 |
-2/3 |
0 |
1 |
|
-Z2 zj-cj |
2/3 |
0 |
-4/3 |
0 |
0 |
|
Wektor X2 zmiennych decyzyjnych ma współrzędne X2 = [x1, x2, x3, x4, x5] = [0, 60, 0, 120, 160]
3. Wartość funkcji celu: ![]()
(pomarańczowy)
4. Elementy zj - cj ostatniego wiersza tabeli (brązowy):
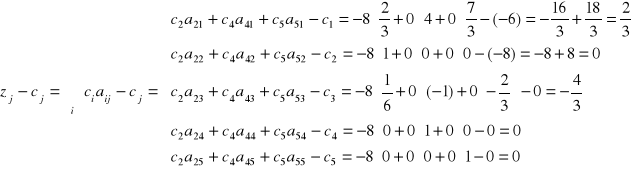
5. W ostatnim wierszu tabeli istnieje zj - cj > 0 dla wektora Aj spoza bazy (dla wektorów bazy zj - cj = 0) i rozwiązanie X2 = [x1, x2, x3, x4, x5] = [0, 60, 0, 120, 160] nie jest optymalne
6. Numer kolumny j = k, dla którego zachodzi: ![]()
to j = k = 1
7. Dla kolumny o numerze j = k =1 ilorazy: 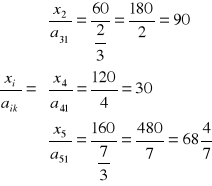
. Numer wiersza i = l, dla którego zachodzi: 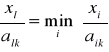
to i = l = 4
8. Nowa tabela w celu otrzymania kolejnego rozwiązania:
a) przepisane bez zmian elementy cj wiersza pierwszego (zielone) oraz oznaczenia wektorów Pj w wierszu drugim (niebieskie);
b) w bazie B (ciemnoniebieskie) w miejsce wektora A4 wpisany wektor A1 a pozostałe wektory bazy przepisane bez zmian;
c) w kolumnie trzeciej (ciemnozielone) wpisane współczynniki wektora wag ci odpowiadające wektorom bazy;
d) pozostałe elementy tablicy:
- elementy Xr (czerwone):
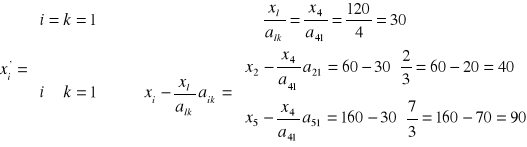
- elementy Pj (niebieskie):
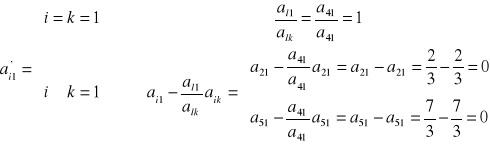
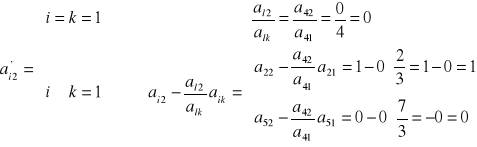
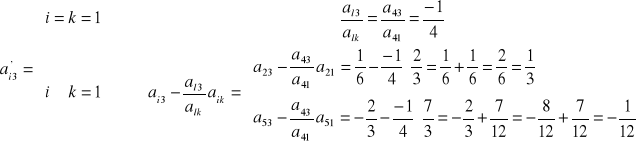
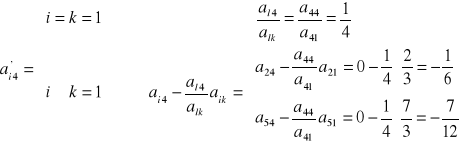
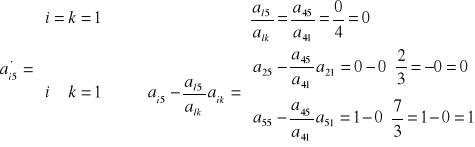
|
|
cj |
-6 |
-8 |
0 |
0 |
0 |
|
B3 |
Aj ci |
A1 |
A2 |
A3 |
A4 |
A5 |
40 |
A2 |
-8 |
0 |
1 |
1/3 |
-1/6 |
0 |
30 |
A1 |
-6 |
1 |
0 |
-1/4 |
1/4 |
0 |
90 |
A5 |
0 |
0 |
0 |
-1/12 |
-7/12 |
1 |
|
-Z3 zj-cj |
0 |
0 |
-7/6 |
-1/6 |
0 |
|
Wektor X3 zmiennych decyzyjnych ma współrzędne X3 = [x1, x2, x3, x4, x5] = [30, 40, 0, 0, 90]
3. Wartość funkcji celu: ![]()
(pomarańczowy)
4. Elementy zj - cj ostatniego wiersza tabeli (brązowy):
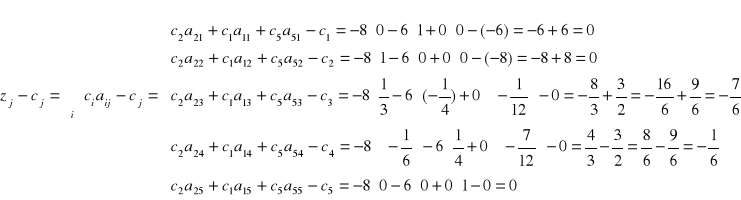
5. W ostatnim wierszu tabeli nie istnieje zj - cj > 0 dla wektora Aj spoza bazy (dla wektorów bazy zj - cj = 0) i rozwiązanie X3 = [x1, x2, x3, x4, x5] = [30, 40, 0, 0, 90] jest optymalne. Wartość funkcji celu jest równa
Z = -min(-Z) = -(-Z3) = 500.
Niezerowa wartość zmiennej decyzyjnej swobodnej x5 wynika z konieczności spełnienia trzeciego równania postaci kanonicznej ograniczeń. Równanie pierwsze i drugie są spełnione przez zmienne decyzyjne rzeczywiste x1 i x2.
Zagadnienie transportowe z kryterium kosztów
W praktyce często spotykamy się z koniecznością dokonania przemieszczenia środków materiałowych (np. transportu zaopatrzenia) z kilku źródeł (magazynów) do kilku miejsc przeznaczenia (odbiorców). Istotne przy tym jest, aby całkowity koszt przewozu był minimalny. Ogólny opis takiego problemu może być następujący:
Dany jest zbiór m dostawców zaopatrujących n odbiorców w jednorodny produkt. Znane są wielkości ai (i = 1, 2, ... , m) zapasów w magazynach oraz wielkości potrzeb odbiorców bj (j = 1, 2, ... , n). Znane są koszty jednostkowe transportu cij produktu z magazynu i do odbiorcy j wyrażone macierzą kosztów C = [cij]m×n
Należy tak zaplanować wielkość dostaw xij z magazynu i do odbiorcy j, aby całkowite koszty transportu były minimalne. Wielkości wszystkich dostaw wyrażone są macierzą dostaw (przydziałów) X = [xij]m×n
Jest to problem decyzyjny typowy dla systemu użytkowania środków transportowych (np. dla transportu samochodowego), w którym kryterium optymalizacji decyzji eksploatacyjnej jest koszt transportu. Uzasadnia to nazwę przedstawionego zagadnienia (problemu).
Jednostkowy koszt transportu powinien dotyczyć kosztów transportu jednostki transportowej produktu, np. pojemności cysterny paliwowej, ładowności samochodu ciężarowego, dopuszczalnej liczby osób przewożonych pojazdem itp. W podobnych jednostkach powinny być wyrażone wielkości zapasów w magazynach i zapotrzebowania odbiorców. Koszty mogą być wyrażone w jednostkach pieniężnych lub za pomocą wielkości do nich proporcjonalnych: zużycia paliwa, odległości, czasu przejazdu (przy założeniu, że jakość dróg, prędkości jazdy pojazdów są jednakowe) itp. Aby problem rozwiązać metodami analitycznymi należy podać jego formalne, matematyczne sformułowanie.
Wyznaczyć macierz zmiennych decyzyjnych X = [xij]m×n, która minimalizuje formę liniową
![]()
przy danych ograniczeniach: ![]()
(suma przydziałów z jednego magazynu nie może przekroczyć wielkości zapasu w tym magazynie)
![]()
(suma przydziałów do jednego odbiorcy nie może przekroczyć wielkości zapotrzebowania tego odbiorcy)
xij ≥ 0
Funkcja celu przedstawia całkowite koszty transportu wyrażone sumą iloczynów kosztów jednostkowych i wielkości dostaw z magazynu i do odbiorcy j.
Aby zapewnić istnienie jednoznacznego rozwiązania układ nierówności ograniczeń należy zamienić na odpowiedni układ równań ograniczeń. W tym przypadku dodatkowo zakłada się konieczność spełnienia tzw. warunku równości podaży i popytu: ![]()
. Jeżeli nie jest on spełniony do zadanego zbioru dostawców lub odbiorców (w zależności od tego czy większa jest podaż czy popyt) dodaje się fikcyjnego dostawcę lub odbiorcę o wielkości zapasu lub zapotrzebowania wynikającej z warunku równości podaży i popytu. Jednostkowe koszty transportu dla takiego fikcyjnego dostawcy lub odbiorcy przyjmuje się jako zerowe, co eliminuje wpływ tego dostawcy lub odbiorcy na funkcję celu.
Jak widać funkcja celu i ograniczenia są funkcjami liniowymi. Jest to więc liniowy problem decyzyjny. Jednakże, ze względu na dużą na ogół liczbę zmiennych decyzyjnych (jest ich m × n) i ograniczeń (jest ich m + n - 1 + m × n: m równań ograniczeń dla odbiorców, n równań ograniczeń dla dostawców, 1 warunek równości podaży i popytu, m × n warunków nieujemności zmiennych decyzyjnych), przedstawione dotychczas metody graficzna (ograniczenie do trzech zmiennych decyzyjnych) i SIMPLEX rozwiązywania zagadnień programowania liniowego są w tym przypadku mało efektywne lub nieprzydatne, zwłaszcza w przypadku rozwiązywania ręcznego. Aby rozwiązać przestawiony transportowy problem decyzyjny metodą SIMPLEX należy dokonać następujących podstawień:
cij = c(i - 1)n + j = ck - przenumerowanie kosztów kolejno wierszami
xij = x(i - 1)n + j = xk - przenumerowanie zmiennych decyzyjnych kolejno wierszami
ai = br = i' = br' - zmiana nazwy i przenumerowanie ograniczeń (potrzeb) odbiorów
bj = br = m + j' = br' - zmiana nazwy i przenumerowanie ograniczeń (zapasów) magazynów
W efekcie funkcja celu przyjmie postać ![]()
a ograniczenia postać ![]()
gdzie rl = 1 dla tych zmiennych decyzyjnych xl które wchodziły do obliczenia warunku br' i rl = 0 dla pozostałych zmiennych decyzyjnych oraz xk ≥ 0, czyli postać wyjściową dla metody SIMPLEX, w tym przypadku bardzo pracochłonną i skomplikowaną.
Dlatego opracowano specjalne metody rozwiązywania problemów transportowych, (kombinatoryczną, MODI (MOdified Distribution Method)). Są one także metodami iteracyjnymi. Polegają na dokonaniu jakiegoś pierwszego wyboru rozwiązania, a następnie dokonywaniu zmian przydziałów od dostawców do odbiorców, dla których funkcja celu przyjmuje coraz mniejszą wartość aż do osiągnięcia rozwiązania optymalnego. Istnieje dość znaczna dowolność wyboru rozwiązania początkowego (metody „kąta północno-zachodniego”, minimalnego kosztu w kolejnych wierszach lub kolumnach, minimalnego elementu macierzy kosztów, VAM itd.), przy czym liczba elementów tego rozwiązania powinna być równa m + n - 1. „Stopień zbliżenia” rozwiązania początkowego do rozwiązania optymalnego ma decydujący wpływ na pracochłonność metody.
Metoda metody rozwiązywania problemów transportowych korzystają z następujących pojęć:
Przekształcenie ekwiwalentne macierzy: niech będzie dana macierz C = [cij]m×n oraz dwa ciągi liczb R = {ri}, i = 1, 2, ... , m (o liczbie wyrazów równej liczbie wierszy macierzy) i S = {sj}, j = 1, 2, ... , n (o liczbie wyrazów równej liczbie kolumn macierzy); macierzą ekwiwalentną do macierzy C nazywa się macierz D = [dij]m×n, której elementy są równe dij = cij + ri + sj
Element macierzy przedstawionej w postaci tablicy dla pary liczb [i,j] (współrzędnych: i i j oznaczają odpowiednio numer wiersza i kolumny tablicy) nazywa się klatką, a dowolny zbiór klatek zestawem
Ciąg klatek, w którym występuje na przemian zmiana wierszy i kolumn nazywa się łańcuchem, np. [1,1] [1,3] [2,3] [2,1] [3,1] ...
Łańcuch zamknięty, którego pierwszy element jest także ostatnim, nazywa się cyklem. Jeżeli w cyklu oznaczy się kolejne klatki na przemian znakami „+” i „-”, to otrzyma się półłańcuch (półcykl) dodatni złożony z klatek z „+” i ujemny złożony z klatek z „-”
|
1 |
2 |
3 |
4 |
|
|
+ |
|
- |
|
|
|
|
|
|
|
|
|
- |
|
|
|
+ |
|
|
|
|
|
|
|
|
|
+ |
|
- |
Zauważmy, że w zagadnieniu transportowym każdej klatce [i,j] odpowiada jeden element macierzy kosztów C i tylko jeden element macierzy dostaw X. Stąd każdy zestaw klatek jest także zestawem elementów cij oraz xij.
Zestaw klatek zawierający co najmniej jeden cykl nazywamy zestawem cyklicznym, nie zawierający cyklu - acyklicznym.
Każde rozwiązanie zagadnienia transportowego X = [xij] dające się przedstawić w formie macierzy, której elementy xij ≠ 0 tworzą zestaw acykliczny, nazywamy rozwiązaniem podstawowym lub bazowym
Elementy xij = 0 rozwiązania X i położone w klatkach acyklicznego zestawu m + n - 1 klatek nazywa się zerami wybranymi
Zbiór niezerowych elementów rozwiązania bazowego X razem z wybranymi zerami, które uzupełniają go do zestawu acyklicznego m + n - 1 klatek, nazywa się wyborem (zbiór m + n klatek jest zawsze cykliczny)
Elementy cij macierzy kosztów C, odpowiadające elementom wyboru, nazywa się elementami wybranymi przez X
Ciąg wyborów X1, X2, ... , Xk jest niezmienny względem ekwiwalentnych przekształceń macierzy kosztów C. Oznacza to, że kolejnych wyborów można dokonywać w macierzy C lub do niej ekwiwalentnej.
Algorytm metody rozwiązania transportowego zagadnienia programowania liniowego z kryterium kosztów jest następujący:
1. Sprawdzić spełnienie warunku równości podaży i popytu: ![]()
- jeżeli podaż jest większa od popytu, to dla jej zrównoważenia do problemu należy wprowadzić dodatkowego fikcyjnego odbiorcę o zapotrzebowaniu ![]()
i kosztach dostaw ci,n+1 = 0
- jeżeli podaż jest mniejsza od popytu, to dla jego zrównoważenia do problemu należy wprowadzić dodatkowy fikcyjny magazyn o wielkości zapasów ![]()
i kosztach dostaw cm+1,j = 0.
Warunki zadania przedstawić w postaci tablicy liczbowej, gdzie jednostkowe koszty dostaw od kolejnych dostawców do kolejnych odbiorców wpisane są w górnym lewym rogu odpowiedniej klatki. W prawym dolnym rogu klatek będą wpisywane wielkości dostaw (przydziałów) - wartości kolejnych zmiennych decyzyjnych.
ai |
b1 |
b2 |
... |
bn |
|
c11 |
c12 |
... |
c1n |
|
|
|
|
|
|
c21 |
c22 |
... |
c2n |
|
|
|
|
|
|
... |
... |
... |
... |
|
|
|
|
|
|
cm1 |
cm2 |
... |
cmn |
|
|
|
|
|
2. Dokonać wyboru pierwszego rozwiązania X1
Metoda „kąta północno-zachodniego” (górnego lewego rogu macierzy kosztów) (bardzo prosta ale prawie nigdy nie daje rozwiązania optymalnego i wymusza wykonania wielu iteracji dla jego otrzymania) - przydział rozpoczyna się od klatki [1,1] w której dokuje się przydziału x11 wpisując jego wartość w prawym dolnym rogu klatki. Możliwe są trzy przypadki:
1. a1 < b1 - zapas dostawcy jest mniejszy od zapotrzebowania odbiorcy - należy dokonać przydziału x11 = a1 i przejść do następnego wiersza (dostawcy), bo zapas dostawcy jest już zerowy
2. a1 > b1 - zapas dostawcy jest większy od zapotrzebowania odbiorcy - należy dokonać przydziału x11 = b1 i przejść w tym wierszu do klatki [1,2] i dokonać przydziału pozostałości zapasu dostawcy a1 = a1 - b1 kolejnemu odbiorcy: x12 = a1 (jeżeli a1 < b2) lub x12 = b2 (jeżeli a1 > b2). W pierwszym przypadku przechodzi się potem do następnego wiersza, w drugim powtarza rozumowanie dla klatki [1,3]. Do następnego wiersza przechodzi się po wyczerpaniu zapasu dostawcy.
3. a1 = b1 (lub reszta w magazynie - dotyczy przypadku 2 - jest równa zapotrzebowaniu kolejnego odbiorcy) - należy dokonać przydziału x11 = a1 i w kolejnej klatce w tym wierszu dokonać przydziału x12 = 0 (tzw. zero wybrane) i przejść do następnego wiersza (dostawcy). Zera wybranego nie wpisuje się w ostatnim wierszu
Po dokonaniu przydziału liczba elementów niezerowych wyboru (wraz z zerami wybranymi) powinna być równa m + n - 1.
Przykład: przydzielić zapasy w zbilansowanym problemie transportowym
Rozpoczynamy od klatki [1,1]: a1 = 150 > 80 = b1 → przydzielamy x11 = b1 = 80 i z pozostałością a1 = a1 - x11 = 150 - 80 = 70 przechodzimy do klatki [1,2]
Dla klatki [1,2]: a1 = 70 > 40 = b2 → przydzielamy x12 = b2 = 40 i z pozostałością a1 = a1 - x11 = 70 - 30 = 30 przechodzimy do klatki [1,3]
Dla klatki [1,3]: a1 = 30 < 100 = b3 → przydzielamy x13 = a1 =30 czyli odbiorca nr 3 ma jeszcze potrzeby b3 = b3 - x13 = 100 - 30 = 70 i aby je zaspokoić przechodzimy do klatki [2,3] (odbiorcy nr 1 i 2 są już zaspokojeni)
Dla klatki [2,3]: a2 = 80 > 70 = b3 → przydzielamy x23 = b3 =70 i z pozostałością a2 = a2 - x23 = 80 - 70 = 10 przechodzimy do klatki [2,4]
Dla klatki [2,4]: a2 = 10 < 80 = b4 → przydzielamy x24 = a2 = 10 czyli odbiorca nr 4 ma jeszcze potrzeby b4 = b4 - x24 = 80 - 10 = 70 i aby je zaspokoić przechodzimy do klatki [3,4] (odbiorcy nr 1, 2 i 3 są już zaspokojeni)
Dla klatki [3,4]: a3 = 70 = 70 = b4 → przydzielamy x34 = b4 = 70 - przydział zakończony
ai |
80 |
40 |
100 |
80 |
|
6 |
10 |
7 |
11 |
|
80 |
40 |
30 |
|
|
8 |
12 |
6 |
17 |
|
|
|
70 |
10 |
|
7 |
8 |
13 |
19 |
|
|
|
|
70 |
Wartość funkcji celu
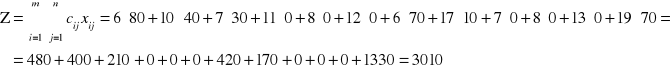
Metoda minimalnego kosztu w kolejnych wierszach (kolumnach) - przydział odbywa się kolejno wierszami z góry lub dołu (kolumnami z lewa lub prawa) w kolejności rosnących kosztów jednostkowych branych dla danego wiersza (kolumny) z uwzględnieniem potrzeb odbiorców, zapasów dostawców i dotychczasowych przydziałów, a w ostatnim wierszu (kolumnie) uzupełnia się brakujące przydziały tak aby wyczerpać zapas dostawców i zaspokoić potrzeby odbiorców. Dokonując przydziału wierszami od góry do dołu w pierwszym wierszu wyznacza się klatkę w której c1j jest najmniejszy. Możliwe są trzy przypadki:
1. a1 < bj - zapas dostawcy jest mniejszy od zapotrzebowania odbiorcy - należy dokonać przydziału x1j = a1 i przejść do następnego wiersza (dostawcy), bo zapas dostawcy jest już zerowy
2. a1 > bj - zapas dostawcy jest większy od zapotrzebowania odbiorcy - należy dokonać przydziału x1j = bj i znaleźć w tym wierszu element c1j o kolejnej większej wartości i dokonać przydziału pozostałości zapasu dostawcy a1 = a1 - bj kolejnemu odbiorcy o tych kolejno większych kosztach: x1j = a1 (jeżeli a1 < bj) lub x1j = bj (jeżeli a1 > bj). W pierwszym przypadku przechodzi się potem do następnego wiersza, w drugim powtarza rozumowanie dla kolejnej klatki z kolejno większymi kosztami. Do następnego wiersza przechodzi się po wyczerpaniu zapasu dostawcy.
3. a1 = bj (lub reszta w magazynie - dotyczy przypadku 2 - jest równa zapotrzebowaniu kolejnego odbiorcy) - należy dokonać przydziału: x1j = a1, po czym znaleźć klatkę w tym wierszu z następnymi wartościami kosztów i dokonać przydziału x12 = 0 (tzw. zero wybrane) i przejść do następnego wiersza (dostawcy). Zera wybranego nie wpisuje się w ostatnim wierszu
W trakcie dokonywania przydziału w kolejnych wierszach należy sprawdzać czy zapotrzebowanie odbiorcy zostało już zaspokojone. Jeżeli tak, w danej kolumnie nie należy dokonywać żadnego przydziału - nawet zera wybranego. W wierszu ostatnim jedynym kryterium przydziału jest równość popytu i podaży. Nie wpisuje się w nim zera wybranego. Po dokonaniu przydziału liczba elementów niezerowych wyboru (wraz z zerami wybranymi) powinna być równa m + n - 1.
Przykład: przydzielić zapasy w zbilansowanym problemie transportowym kolejno wierszami z góry na dół
Rozpoczynamy od wiersza pierwszego dla którego najmniejszym kosztem jest 6 z klatki [1,1]: a1 = 150 > 80 = b1 → przydzielamy x11 = b1 = 80 i z pozostałością a1 = a1 - x11 = 150 - 80 = 70 przechodzimy do klatki z kolejno większym kosztem (7) czyli klatki [1,3]
Dla klatki [1,3]: a1 = 70 < 100 = b3 → przydzielamy x13 = a1 =70 czyli odbiorca nr 3 ma jeszcze potrzeby b3 = b3 - x13 = 100 - 70 = 30 i aby je zaspokoić przechodzimy do wiersza drugiego
W wierszu drugim najmniejszym kosztem jest 6 z klatki [2,3]: a2 = 80 < 30 = b3 → przydzielamy x12 = b3 = 30 i z pozostałością a2 = a2 - x23 = 80 - 30 = 50 przechodzimy do klatki z kolejno większym kosztem (8) czyli klatki [2,1]
Odbiorca nr 1 jest już zaspokojony - nie przydzielamy niczego i przechodzimy do klatki z kolejno większym kosztem (12) czyli klatki [2,2]
Dla klatki [2,2]: a2 = 50 > 40 = b2 → przydzielamy x22 = b2 =40 i z pozostałością a2 = a2 - x22 = 50 - 40 = 10 przechodzimy do z kolejno większym kosztem (17) czyli klatki [2,4]
Dla klatki [2,4]: a2 = 10 < 80 = b4 → przydzielamy x24 = a2 = 10 czyli odbiorca nr 4 ma jeszcze potrzeby b4 = b4 - x24 = 80 - 10 = 70 i aby je zaspokoić przechodzimy kolejnego wiersza
Jest to ostatni wiersz - uzupełniamy potrzeby: odbiorcy nr 1,2 i 3 są już zaspokojeni, przydzielamy brakujące potrzeby odbiorcy nr 4: dla klatki [3,4]: x34 = b4 = 70 - przydział zakończony
ai |
80 |
40 |
100 |
80 |
|
6 |
10 |
7 |
11 |
|
80 |
|
70 |
|
|
8 |
12 |
6 |
17 |
|
|
40 |
30 |
10 |
|
7 |
8 |
13 |
19 |
|
|
|
|
70 |
Wartość funkcji celu
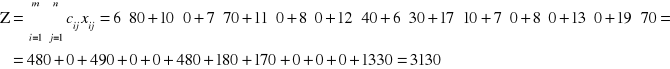
Metoda minimalnego elementu macierzy kosztów - przydział następuje w kolejności rosnących kosztów jednostkowych branych dla całej tabeli, z uwzględnieniem potrzeb odbiorców, zapasów dostawców i dotychczasowych przydziałów. Możliwe są trzy przypadki:
1. ai < bj - zapas dostawcy jest mniejszy od zapotrzebowania odbiorcy - należy dokonać przydziału xij = ai i przejść do kolejnej klatki o kolejno większych kosztach, oznaczając jednocześnie dostawcę ai jako pustego, o zerowym zapasie (nie można od niego niczego przydzielić)
2. ai > bj - zapas dostawcy jest większy od zapotrzebowania odbiorcy - należy dokonać przydziału xij = bj i znaleźć w tym wierszu element cij o kolejnej większej wartości i dokonać przydziału pozostałości zapasu dostawcy ai = ai - bj kolejnemu odbiorcy o tych kolejno większych kosztach: xij = ai (jeżeli ai < bj) lub xij = bj (jeżeli ai > bj). W pierwszym przypadku przechodzi się potem do następnej klatki z kolejno większymi kosztami, w drugim powtarza rozumowanie dla kolejnej klatki z kolejno większymi kosztami.
3. ai = bj (lub reszta w magazynie - dotyczy przypadku 2 - jest równa zapotrzebowaniu kolejnego odbiorcy) - należy dokonać przydziału: xij = ai, po czym znaleźć klatkę w tym samym wierszu lub kolumnie z kolejną wartością kosztów i dokonać przydziału x12 = 0 (tzw. zero wybrane) i przejść do następnej klatki. Zera wybranego nie wpisuje się w ostatnim przydziale
W trakcie dokonywania przydziału w kolejnych klatkach należy sprawdzać czy zapotrzebowanie odbiorcy zostało już zaspokojone i czy zapasy dostawcy zostały już wyczerpane. Jeżeli tak, w danej kolumnie lub wierszu nie należy dokonywać żadnego przydziału - nawet zera wybranego. Po dokonaniu przydziału liczba elementów niezerowych wyboru (wraz z zerami wybranymi) powinna być równa m + n - 1.
Przykład: przydzielić zapasy w zbilansowanym problemie transportowym
Najmniejszym kosztem w tabeli jest 6 z klatek [1,1] i [2,3]:
- dla [1,1]: a1 = 150 > 80 = b1 → przydzielamy x11 = b1 = 80, u dostawcy jest pozostałość a1 = a1 - x11 = 150 - 80 = 70, odbiorca nr 1 jest zaspokojony - oznaczamy klatki [2,1] i [3,1] jakimś symbolem, np. „#” aby je pomijać przy kolejnych przydziałach
-dla [2,3]: a2 = 80 < 100 = b3 → przydzielamy x23 = a2 = 80, dostawca nr 2 jest wyczerpany - oznaczamy klatki [2,1], [2,2] i [2,3] jakimś symbolem, np. „#” aby je pomijać przy kolejnych przydziałach, u odbiorcy nr 3 jest pozostałość b3 = b3 - x23 = 100 - 80 = 20
Kolejno większym kosztem jest 7 z klatek [1,3] i [3,1]:
- dla [1,3]: a1 = 70 > 20 = b3 → przydzielamy x13 = b3 = 20, u dostawcy jest pozostałość a1 = a1 - x13 = 70 - 20 = 50, odbiorca nr 3 jest zaspokojony - oznaczamy klatkę [3,3] jakimś symbolem, np. „#” aby ją pomijać przy kolejnych przydziałach
- klatka [3,1] jest już zapisana symbolem #
Kolejno większym kosztem jest 8 z klatek [2,1] i [3,2]:
- klatka [2,1] jest już zapisana symbolem #
- dla [3,2]: a3 = 70 > 40 = b2 → przydzielamy x23 = b2 = 40, u dostawcy jest pozostałość a3 = a3 - x23 = 70 - 40 = 30, odbiorca nr 2 jest zaspokojony - oznaczamy klatk1 [1,2] i [2,2] jakimś symbolem, np. „#” aby je pomijać przy kolejnych przydziałach
Kolejno większym kosztem jest 10 z klatki [2,2], jest już ona zapisana symbolem #
Kolejno większym kosztem jest 11 z klatki [1,4]: a1 = 50 < 80 = b4 → przydzielamy x14 = a1 = 50, dostawca nr 1 jest wyczerpany, u odbiorcy nr 4 jest pozostałość b4 = b4 - x14 = 80 - 50 = 30
W tabeli pozostała tylko jedna klatka bez wpisanego przydziału: [3,4] - uzupełniamy ją o zapasy dostawczy nr 3 i potrzeby odbiorcy nr 4: x34 = a3 = b4 = 30 - przydział zakończony
ai |
80 |
40 |
100 |
80 |
|
6 |
10 |
7 |
11 |
|
80 |
# |
20 |
50 |
|
8 |
12 |
6 |
17 |
|
# |
# |
80 |
# |
|
7 |
8 |
13 |
19 |
|
# |
40 |
# |
30 |
Wartość funkcji celu

Metoda VAM (Vogel's approximation method) (dość skomplikowana ale prawie zawsze daje rozwiązanie optymalne i nie wymusza wykonania iteracji dla jego otrzymania) - przydział następuje w kolejności rosnących przyrostów kosztów jednostkowych wyznaczonych dla jeszcze nie zapisanych przydziałami wierszy i kolumn odpowiadających kosztom najniższym i kolejno wyższym (aby maksymalizować przydziały dla niskich kosztów i minimalizować ewentualny przydział dla relatywnie dużo większych kosztów), z uwzględnieniem potrzeb odbiorców, zapasów dostawców i dotychczasowych przydziałów. Dla wiersza lub kolumny o największym przyroście kosztów dokonuje się przydziału w klatce o kosztach najniższych. Możliwe są trzy przypadki:
1. ai < bj - zapas dostawcy jest mniejszy od zapotrzebowania odbiorcy - należy dokonać przydziału xij = ai i wyznaczyć od nowa przyrosty kosztów ignorując wiersz o numerze i (zapas dostawcy i wyczerpany)
2. ai > bj - zapas dostawcy jest większy od zapotrzebowania odbiorcy - należy dokonać przydziału xij = bj i wyznaczyć od nowa przyrosty kosztów ignorując kolumnę o numerze j (potrzeby odbiorcy j zaspokojone)
3. ai = bj - należy dokonać przydziału: xij = ai = bj i wyznaczyć od nowa przyrosty kosztów ignorując wiersz o numerze i i kolumnę o numerze j
Po dokonaniu przydziału liczba elementów niezerowych wyboru (wraz z zerami wybranymi) powinna być równa m + n - 1.
Przykład: przydzielić zapasy w zbilansowanym problemie transportowym
Po obliczeniu różnic między najmniejszym kosztem i kosztem kolejno większym dla wszystkich wierszy i kolumn (wyniki obok i pod tabelą) okazało się że największym przyrostem jest 6 dla kolumny nr 4. Do klatki z najmniejszym kosztem w tej kolumnie czyli klatki [1,4] zachodzi a1 = 150 > 80 = b4 → przydzielamy x14 = b4 = 80 i wyznaczamy od nowa przyrosty kosztów ignorując kolumnę nr 4 (potrzeby odbiorcy 4 zaspokojone) pamiętając że w magazynie 1 zostało a1 = a1 - x14 = 150 - 80 = 70
ai |
80 |
40 |
100 |
80 |
|
|
6 |
10 |
7 |
11 |
|6-7|=1 |
|
|
|
|
80 |
|
|
8 |
12 |
6 |
17 |
|6-8|=2 |
|
|
|
|
|
|
|
7 |
8 |
13 |
19 |
|7-8|=1 |
|
|
|
|
|
|
|
|6-7|=1 |
|8-10|=2 |
|6-7|=1 |
|11-17|=6 |
|
Po obliczeniu różnic między najmniejszym kosztem i kosztem kolejno większym dla wszystkich rozpatrywanych wierszy i kolumn (wyniki obok i pod tabelą) okazało się że największym przyrostem jest 2 dla kolumny nr 2 i wiersza nr 2. Do dokonania przydziału wybieramy arbitralnie wiersz nr 2. Do klatki z najmniejszym kosztem w tym wierszu czyli klatki [2,3] zachodzi a2 = 80 < 100 = b3 → przydzielamy x23 = a2 = 80 i wyznaczamy od nowa przyrosty kosztów ignorując kolumnę nr 4 (potrzeby odbiorcy 4 zaspokojone) i wiersz nr 2 (zapas dostawcy 2 wyczerpany) pamiętając że odbiorca 3 ma jeszcze potrzeby b3 = b3 - x23 = 100 - 80 = 20
ai |
80 |
40 |
100 |
80 |
|
|
6 |
10 |
7 |
11 |
|6-7|=1 |
|
|
|
|
80 |
|
|
8 |
12 |
6 |
|
|6-8|=2 |
|
|
|
80 |
|
|
|
7 |
8 |
13 |
|
|7-8|=1 |
|
|
|
|
|
|
|
|6-7|=1 |
|8-10|=2 |
|6-7|=1 |
X |
|
Po obliczeniu różnic między najmniejszym kosztem i kosztem kolejno większym dla wszystkich rozpatrywanych wierszy i kolumn (wyniki obok i pod tabelą) okazało się że największym przyrostem jest 6 dla kolumny nr 3. Do klatki z najmniejszym kosztem w tej kolumnie czyli klatki [1,3] zachodzi a1 = 70 > 20 = b3 → przydzielamy x13 = b3 = 20 i wyznaczamy od nowa przyrosty kosztów ignorując kolumny nr 3 i 4 (potrzeby odbiorcy 3 i 4 zaspokojone) i wiersz nr 2 (zapas dostawcy 2 wyczerpany) pamiętając że w magazynie 1 zostało a1 = a1 - x13 = 70 - 20 = 50
ai |
80 |
40 |
100 |
80 |
|
|
6 |
10 |
7 |
11 |
|6-7|=1 |
|
|
|
20 |
80 |
|
|
|
|
6 |
|
X |
|
|
|
80 |
|
|
|
7 |
8 |
13 |
|
|7-8|=1 |
|
|
|
|
|
|
|
|6-7|=1 |
|8-10|=2 |
|7-13|=6 |
X |
|
Po obliczeniu różnic między najmniejszym kosztem i kosztem kolejno większym dla wszystkich rozpatrywanych wierszy i kolumn (wyniki obok i pod tabelą) okazało się że największym przyrostem jest 4 dla wiersza nr 1. Do klatki z najmniejszym kosztem w tej kolumnie czyli klatki [1,1] zachodzi a1 = 50 < 80 = b1 → przydzielamy x11 = a1 = 50 i wyznaczamy od nowa przyrosty kosztów ignorując kolumny nr 3 i 4 (potrzeby odbiorcy 3 i 4 zaspokojone) i wiersze nr 1 i 2 (zapas dostawcy 1 i 2 wyczerpany) pamiętając że odbiorca 1 ma jeszcze potrzeby b1 = b1 - x11 = 80 - 50 = 30
ai |
80 |
40 |
100 |
80 |
|
|
6 |
10 |
7 |
11 |
|6-10|=4 |
|
50 |
|
20 |
80 |
|
|
|
|
6 |
|
X |
|
|
|
80 |
|
|
|
7 |
8 |
|
|
|7-8|=1 |
|
|
|
|
|
|
|
|6-7|=1 |
|8-10|=2 |
X |
X |
|
Przy obliczaniu różnic między najmniejszym kosztem i kosztem kolejno większym dla wszystkich rozpatrywanych wierszy i kolumn (wyniki obok i pod tabelą) okazało się że nie można wyznaczyć tych przyrostów dla kolumn, gdyż w tabeli zostały tylko dwa rozpatrywane koszty w trzecim wierszu - w wierszu tym przydzielamy zapasy do klatek z tymi pozostałymi kosztami zgodnie z rosnącymi kosztami i uwzględniając zapasy pozostałe w magazynach i pozostałe potrzeby odbiorców:
- klatką z najmniejszym kosztem 7 jest [3,1]: a3 = 70 > 30 = b1 → przydzielamy x31 = b1 = 30, w magazynie 3 pozostało a3 = a3 - x31 = 70 - 30 = 40
- klatką z kolejno większym kosztem 8 jest [3,2]: a3 = 40 = b2 → przydzielamy x32 = a3 = b2 = 40, w magazynie 3 pozostało a3 = a3 - x32 = 40 - 40 = 0 - przydział zakończony
ai |
80 |
40 |
100 |
80 |
|
|
6 |
|
7 |
11 |
X |
|
50 |
|
20 |
80 |
|
|
|
|
6 |
|
X |
|
|
|
80 |
|
|
|
7 |
8 |
|
|
|7-8|=1 |
|
30 |
40 |
|
|
|
|
|7-?|=? |
|8-?|=? |
X |
X |
|
Wartość funkcji celu
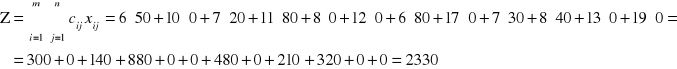
3. Wykonać przekształcenie ekwiwalentne macierzy kosztów w taki sposób, aby koszty w klatkach z przydziałami xij ≠ 0 lub xij = „0 wybrane” (klatkach wybranych) określonymi dla rozwiązania Xr wyzerowały się. Wyrazy ciągów R = {ri} i S = {sj} można znaleźć rozwiązując układ równań ![]()
gdzie ![]()
są kosztami w klatkach wybranych. Ponieważ układ ten składa się z m + n - 1 równań (tyle jest kosztów ![]()
), a niewiadomych jest m + n (tyle jest poszukiwanych liczb ri i sj), można go rozwiązać w funkcji jednej z niewiadomych przyjmując jej wartość. Najczęściej przyjmuje się r1 = 0 (co wydaje się po prostu najprostsze).
W wyniku ekwiwalentnego przekształcenia macierzy kosztów otrzyma się sytuację następującą: jednostkowe koszty transportu w klatkach wybranych przez przydział (rozwiązanie) Xr są równe zero ![]()
a jednostkowe koszty transportu w klatkach nie wybranych przez przydział Xr są dodatnie, zerowe lub ujemne (zależnie od rozwiązywanego zagadnienia). W efekcie funkcja celu obliczona dla takich nowych kosztów i aktualnego przydziału ![]()
bo jest sumą iloczynów zerowych kosztów i na ogół niezerowych przydziałów (dla klatek wybranych przez rozwiązanie Xr) oraz na ogół niezerowych kosztów i zerowych przydziałów (dla klatek nie wybranych przez rozwiązanie Xr). Jeżeli w przekształconej macierzy kosztów występują wartości ujemne, to oznacza, że gdyby zmienić rozwiązanie tak aby zrealizować przydział od dostawcy do odbiorcy o takich ujemnych kosztach jednostkowych to funkcja celu ![]()
bo była by sumą iloczynów ujemnych i zerowych kosztów i na ogół niezerowych przydziałów (dla klatek wybranych przez nowe rozwiązanie Xr+1) oraz na ogół niezerowych kosztów i zerowych przydziałów (dla klatek nie wybranych przez nowe rozwiązanie Xr+1), czyli dokonano by optymalizacji rozwiązania przez lepsze spełnienie celu ![]()
. Stąd kryterium wykonania kolejnej iteracji w algorytmie metody rozwiązania transportowego zagadnienia programowania liniowego z kryterium kosztów jest następujące:
Jeżeli w wyniku dokonanego przekształcenia ekwiwalentnego macierzy kosztów pozostałe elementy macierzy kosztów (te w klatkach wybranych są oczywiście zerami) są:
- nieujemne (cij ≥ 0) to otrzymane rozwiązanie Xr jest optymalne
- zerowe (cij = 0) to istnieją inne rozwiązania o tej samej wartości funkcji celu
- ujemne (cij < 0) to otrzymane rozwiązanie Xr nie jest optymalne i należy dokonać optymalizacji rozwiązania poprzez odpowiednią zmianę przydziału zapasów od dostawców do odbiorców
4. Spośród ujemnych elementów cij ekwiwalentnie przekształconej, nowej macierzy kosztów znaleźć element najmniejszy. Klatkę, w której ten element występuje oznaczyć znakiem „+”.
5. Rozpoczynając od tej klatki oznaczonej „+”, w oparciu o elementy wybrane przez aktualny przydział (niekoniecznie wszystkie) zbudować cykl rozładowujący, oznaczając na przemian klatki tego cyklu znakami „-” i „+”. Otrzyma się w ten sposób półłańcuchy dodatni i ujemny.
6. W półłańcuchu ujemnym znaleźć najmniejszą wartość dostaw xij (może to być zero wybrane) i przenieść tę wartość po wszystkich klatkach cyklu, dodając lub odejmując ją zgodnie ze znakiem klatki do aktualnej wartości xij dostawy w danej klatce otrzymując nowe zoptymalizowane wartości przydziałów. W ten sposób uzyskuje się kolejne rozwiązanie Xr+1 zagadnienia transportowego z kryterium kosztów, ponieważ zmienione zostały wartości zmiennych decyzyjnych.
7. Zbudować nową tablicę, wpisując do niej elementy przekształconej ekwiwalentnie macierzy kosztów oraz elementy zmienionego, nowego rozwiązania Xr+1 (wraz z zerami wybranymi powinno ich być m + n - 1) i powrócić do punktu 3. algorytmu.
W każdym kroku rozwiązania wartość rzeczywistej funkcji celu można wyznaczyć tylko na podstawie wyjściowej macierzy kosztów i elementów danego wyboru. Jeżeli w trakcie realizacji punktu 3. algorytmu okaże się, że otrzymane rozwiązanie jest optymalne, to właśnie tak otrzymuje się minimalną wartość funkcji celu, czyli najmniejsze koszty realizacji dostawy od wszystkich dostawców do wszystkich odbiorców.
Przykład
Zaplanować wartości dostaw (wyrażone w jednostkach transportowych, np. liczby palet całopojazdowych) od dostawców o zapasach ai = {10, 15, 25} do odbiorców o potrzebach bj = {5, 10, 20, 15} dla kosztów jednostkowych transportu (wyrażonych w jednostkach kosztu) przedstawionych w następującej macierzy 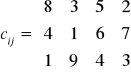
Algorytm metody rozwiązania transportowego zagadnienia programowania liniowego z kryterium kosztów
1. Warunek równości podaży i popytu jest spełniony: ![]()
Warunki zadania przedstawiamy w postaci tablicy liczbowej
ai |
5 |
10 |
20 |
15 |
|
8 |
3 |
5 |
2 |
|
|
|
|
10 |
|
4 |
1 |
6 |
7 |
|
5 |
10 |
0 |
|
|
1 |
9 |
4 |
3 |
|
|
|
20 |
5 |
2. Wybór pierwszego rozwiązania metodą minimalnego kosztu w kolejnych wierszach od góry w dół:
- W wierszu pierwszym najmniejszym kosztem jest c14 = 2. Ponieważ a1 < b4 (10 < 15) w klatce [1,4] dokonujemy przydziału x14 = 10 i przechodzimy do wiersza drugiego
- W wierszu drugim najmniejszym kosztem jest c22 = 1. Ponieważ a2 > b2 (15 > 10) w klatce [2,2] dokonujemy przydziału x22 = 10. U dostawcy drugiego pozostało a2 = a2 - b2 =15 - 10 = 5 jednostek zapasu. Klatką z kolejno większym kosztem c21 = 4 jest klatka [2,1]. Ponieważ a2 = b1 (5 = 5) w klatce [2,1] dokonujemy przydziału x21 = 5 i w klatce z kolejno większymi kosztami, czyli [2,3] dokonujemy przydziału zera wybranego: x23 = 0
- w wierszu trzecim (ostatnim) dokonujemy przydziału według kryterium zrównoważenia popytu odbiorców: pierwszy odbiorca zaspokojony, drugi odbiorca zaspokojony, trzeciemu odbiorcy brakuje x33 = 20, czwartemu odbiorcy brakuje x34 = 5
Wszystkich elementów wyboru jest m + n - 1 = 6.
3. Przekształcenie ekwiwalentne macierzy kosztów takie, aby koszty w klatkach przydziałem przyjęły wartość równą zero: ![]()
Przyjmujemy wartość wyrazu r1 = 0 i zapisujemy układ m + n - 1 równań w celu wyznaczenia pozostałych wyrazów ciągów R i S:
r1 = 0
c14 + r1 + s4 = 2 + r1 + s4 = 0 → s4 = -2
c21 + r2 + s1 = 4 + r2 + s1 = 0 → s1 = -1
c22 + r2 + s2 = 1 + r2 + s2 = 0 → s2 = 2
c23 + r2 + s3 = 6 + r2 + s3 = 0 → r2 = -3
c33 + r3 + s3 = 4 + r3 + s3 = 0 → s3 = -3
c34 + r3 + s4 = 3 + r3 + s4 = 0 → r3 = -1
R = {0,-3,-1} i S = {-1,2,-3,-2}
Dla klatek wybranych ![]()
Dla pozostałych: c11 + r1 + s1 = 8 + 0 - 1 = 7
c12 + r1 + s2 = 3 + 0 + 2 = 5
c13 + r1 + s3 = 5 + 0 - 3 = 2
c24 + r2 + s4 = 7 - 3 - 2 = 2
c31 + r3 + s1 = 1 - 1 - 1 = -1
c32 + r1 + s1 = 9 - 1 + 2 = 10
ai |
5 |
10 |
20 |
15 |
|
7 |
5 |
2 |
0 |
|
|
|
|
10 |
|
0 |
0 |
0 |
2 |
|
⊖ 5 |
10 |
⊕ 5 0 |
|
|
-1 |
10 |
0 |
0 |
|
⊕ 5. |
|
⊖ 15 20 |
5 |
W ekwiwalentnie przekształconej macierzy kosztów znajduje się jeden element o wartości ujemnej c31 = -1, co oznacza, że rozwiązanie nie jest optymalne
4. Klatkę [3,1] oznaczamy znakiem „+” .
5. W oparciu o klatki zawierające elementy wybrane budujemy cykl rozpoczynając od wymienionej klatki [3,1]. W naszej tablicy jedynym możliwym do utworzenia jest cykl składający się z klatek [3,1] [2,1] [2,3] [3,3] [3,1]. Klatki cyklu oznaczamy na przemian znakami „-” i „+”.
6. Najmniejszą wartością dostaw w półłańcuchu ujemnym jest x21 = 5. Przenosimy ten element po wszystkich klatkach cyklu, dodając lub odejmując go od wartości xij. Poprzednie wartości xij skreślamy, a nowe wartości x31 = 5, x21 = 0 (zwykłe, nie wybrane, nie wpisywane do tabeli), x31 = 5 i x33 = 15 wpisujemy obok.
7. Po uzyskaniu nowego rozwiązania budujemy kolejną tabelę. Należy zwrócić uwagę, aby znalazło się w niej m + n - 1 elementów wybranych.
ai |
5 |
10 |
20 |
15 |
|
7 |
5 |
2 |
0 |
|
|
|
|
10 |
|
0 |
0 |
0 |
2 |
|
|
10 |
5 |
|
|
-1 |
10 |
0 |
0 |
|
5 |
|
15 |
5 |
3. Przekształcenie ekwiwalentne macierzy kosztów takie, aby koszty w klatkach przydziałem przyjęły wartość równą zero: ![]()
Przyjmujemy wartość wyrazu r1 = 0 i zapisujemy układ m + n - 1 równań w celu wyznaczenia pozostałych wyrazów ciągów R i S:
r1 = 0
c14 + r1 + s4 = 0 + r1 + s4 = 0 → s4 = 0
c22 + r2 + s2 = 0 + r2 + s2 = 0 → s2 = 0
c23 + r2 + s3 = 0 + r2 + s3 = 0 → r2 = 0
c31 + r3 + s1 = -1 + r3 + s1 = 0 → s1 = 1
c33 + r3 + s3 = 0 + r3 + s3 = 0 → s3 = 0
c34 + r3 + s4 = 0 + r3 + s4 = 0 → r3 = 0
R = {0,0,0} i S = {1,0,0,0}
Dla klatek wybranych ![]()
Dla pozostałych: c11 + r1 + s1 = 7 + 0 + 1 = 8
c12 + r1 + s2 = 5 + 0 + 0 = 5
c13 + r1 + s3 = 2 + 0 + 0 = 2
c21 + r2 + s1 = 0 + 0 + 1 = 1
c24 + r2 + s4 = 2 + 0 + 0 = 2
c32 + r3 + s2 = 10 + 0 + 0 = 10
ai |
5 |
10 |
20 |
15 |
|
8 |
5 |
2 |
0 |
|
|
|
|
10 |
|
1 |
0 |
0 |
2 |
|
|
10 |
5 |
|
|
0 |
10 |
0 |
0 |
|
5 |
|
15 |
5 |
W ekwiwalentnie przekształconej macierzy kosztów nie ma elementów ujemnych, co oznacza, że aktualne rozwiązanie jest optymalne. Nie istnieją też zerowe koszty w klatkach nie wybranych. Zagadnienie ma więc tylko jedno rozwiązanie optymalne. Wartość funkcji celu obliczamy zestawiając w końcowej tabeli wyjściową macierz kosztów i rozwiązanie optymalne
ai |
5 |
10 |
20 |
15 |
|
8 |
3 |
5 |
2 |
|
|
|
|
10 |
|
4 |
1 |
6 |
7 |
|
|
10 |
5 |
|
|
1 |
9 |
4 |
3 |
|
5 |
|
15 |
5 |
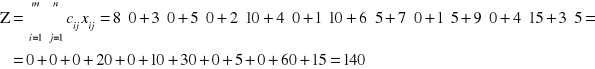
Dla porównania, wartości funkcji celu dla pierwszego rozwiązania była równa
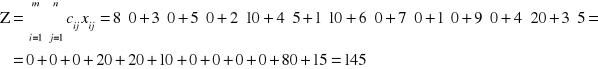
Zagadnienie transportowe z kryterium czasu
Sformułowanie problemu transportowego z kryterium czasu jest bardzo podobne do sformułowania problemu transportowego z kryterium kosztów. Problem transportowy dotyczy wyboru takiego sposobu realizacji dostaw zapasów od m dostawców do n odbiorców, aby czas tej realizacji był najkrótszy. Dana jest macierz czasów realizacji dostaw T = [tij]m×n od dostawców i do odbiorców j. Zakłada się tu, że liczba środków transportowych jest wystarczająca do jednorazowej realizacji dostaw wszystkich zapasów.
Ograniczenia problemu transportowego z kryterium czasu są identyczne jak w problemie transportowym z kryterium kosztów: ![]()
![]()
![]()
Obowiązuje także warunek równości podaży i popytu
Sama funkcja celu ma jednak trochę inną postać. Dla kryterium kosztów na koszt realizacji dostawy składają się koszty realizacji wszystkich dostaw od wszystkich dostawców do wszystkich odbiorców, stąd funkcja cela ma postać odpowiedniej sumy. Dla kryterium czasu czasem realizacji dostawy jest czas najdłuższej dostawy dla danego przydziału (rozwiązania) X: ![]()
gdzie pod uwagę bierze się tylko czasy tij z klatek z dodatnimi wartościami dostawy zapasu xij > 0 (czasy z klatek bez przydziałów nie wpływają na czas realizacji dostawy).
Spośród wszystkich możliwych rozwiązań realizacji dostaw X optymalne Xopt będzie to, dla którego czas tX ma wartość minimalną ![]()
gdzie Ω jest zbiorem tych możliwych rozwiązań (zbiorem rozwiązań dopuszczalnych zagadnienia transportowego).
Ostatecznie funkcję celu zagadnienia transportowego z kryterium czasu można zapisać w postaci ![]()
Algorytm metody rozwiązania transportowego zagadnienia programowania liniowego z kryterium czasu jest następujący:
1. Sprawdzić spełnienie warunku równości podaży i popytu. Zapisać problem w tablicy liczbowej (jak dla kryterium kosztów).
2. Dokonać wyboru pierwszego rozwiązania (jak dla kryterium kosztów z wyjątkiem konieczności wpisywania zer wybranych).
3. Dla aktualnego rozwiązania Xr wybrać czas ![]()
i usunąć (wykreślić) z tablicy wszystkie klatki, w których czas tij > tX. Ma to na celu przestanie zajmowania się klatkami, do których przydział może tylko zwiększyć czas realizacji dostawy, a więc pogorszyć optymalność kolejnego rozwiązania. Klatkę, w której ten czas występuje oznaczyć znakiem „-”.
4. Rozpoczynając od tej klatki oznaczonej „-”, w oparciu o klatki nie wykreślone z tablicy (niekoniecznie wszystkie) zbudować cykl rozładowujący, oznaczając na przemian klatki tego cyklu znakami „+” i „-”. Otrzyma się w ten sposób półłańcuchy dodatni i ujemny.
5. W półłańcuchu ujemnym znaleźć najmniejszą ale niezerową wartość dostaw xij i przenieść tę wartość po wszystkich klatkach cyklu, dodając lub odejmując ją zgodnie ze znakiem klatki do aktualnej wartości xij dostawy w danej klatce otrzymując nowe wartości przydziałów.
Jeżeli przenoszony przydział ![]()
ma wartość równą wartości znajdującej się w rozładowywanej klatce zawierającej czas tX to otrzymuje się nowe rozwiązanie Xr+1 o mniejszym czasie realizacji.
Jeżeli przenoszony przydział ![]()
ma wartość mniejszą od wartości znajdującej się w rozładowywanej klatce zawierającej czas tX to należy budować, o ile jest to możliwe, kolejne cykle rozładowujące aż do całkowitego rozładowania klatki zawierającej czas tX, tj. aż do otrzymania nowego rozwiązania Xr+1 o mniejszym czasie realizacji.
Jeżeli nie można zbudować cyklu rozładowującego (zerującego wartość przydziału w klatce zawierającej czas tX) to otrzymane rozwiązanie jest optymalne.
6. Zbudować nową tablicę, zaznaczając w niej klatki wykreślone i wpisując do niej (do niewykreślonych klatek) elementy macierzy czasu i elementy zmienionego, nowego rozwiązania Xr+1 i powrócić do punktu 3 algorytmu.
Przykład
Zaplanować wartości dostaw (wyrażone w jednostkach transportowych, np. liczby palet całopojazdowych) od dostawców o zapasach ai = {10, 15, 25} do odbiorców o potrzebach bj = {5, 10, 20, 15} dla czasów transportu (wyrażonych w jednostkach czasu) przedstawionych w następującej macierzy 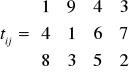
Algorytm metody rozwiązania transportowego zagadnienia programowania liniowego z kryterium czasu
1. Warunek równości podaży i popytu jest spełniony ![]()
Warunki zadania przedstawiamy w postaci tablicy liczbowej
2. Wybór pierwszego rozwiązania metodą minimalnego kosztu w kolejnych wierszach od góry w dół:
- W wierszu pierwszym najkrótszym czasem jest t11 = 1. Ponieważ a1 > b1 (10 > 5) w klatce [1,1] dokonujemy przydziału x31 = 5. U dostawcy pierwszego pozostało a1 = a1 - b1 =10 - 5 = 5 jednostek zapasu. Klatką z kolejno większym czasem t14 = 3 jest klatka [1,4]. Ponieważ a1 < b4 (5 < 15) w klatce [1,4] dokonujemy przydziału x14 = 5 i przechodzimy do wiersza drugiego
- W wierszu drugim najmniejszym czasem jest t22 = 1. Ponieważ a2 > b2 (15 > 10) w klatce [2,2] dokonujemy przydziału x22 = 10. U dostawcy drugiego pozostało a2 = a2 - b2 =15 - 10 = 5 jednostek zapasu. Klatką z kolejno większym czasem t21 = 4 jest klatka [2,1], ale potrzeby odbiorcy pierwszego są już zaspokojone więc przechodzimy do klatki z kolejno większym czasem. Klatką tą jest [2,3]. Ponieważ a2 < b3 (5 < 20) w klatce [2,3] dokonujemy przydziału x23 = 5 i przechodzimy do wiersza trzeciego
- w wierszu trzecim (ostatnim) dokonujemy przydziału według kryterium zrównoważenia popytu odbiorców: pierwszy odbiorca zaspokojony, drugi odbiorca zaspokojony, trzeciemu odbiorcy brakuje x33 = 15, czwartemu odbiorcy brakuje x34 = 10
ai |
5 |
10 |
20 |
15 |
|
1 |
9 |
4 |
3 |
|
⊖ 5 |
|
⊕ 5 |
5 |
|
4 |
1 |
6 |
7 |
|
⊕ 5 |
10 |
⊖ 5 |
|
|
8 |
3 |
5 |
2 |
|
|
|
15 |
10 |
3. Najdłuższym czasem dostawy jest t23 = 6. Wykreślamy z tablicy klatki zawierające czasy dłuższe - są to klatki z t12 = 9, t24 = 7, t31 = 8). Klatkę [2,3] oznaczamy znakiem „-”.
4. Rozpoczynając od klatki [2,3] oznaczonej „-”, w oparciu o klatki nie wykreślone z tablicy (niekoniecznie wszystkie) budujemy cykle rozładowujące. Możliwy cykl [2,3] [3,3] [3,2] [2,2] [2,3] nie jest cyklem rozładowującym, ponieważ najmniejszą wartością przydziału w półłańcuchu ujemnym byłby przydział x32 = 0, a przenoszenie zera nie zmienia rozwiązania. Cyklem rozładowującym jest [2,3] [2,1] [1,1] [1,3] [2,3].
5. W półłańcuchu ujemnym najmniejszą ale niezerową wartością dostaw jest x23 = x11 = 5. Przenosimy ten element po wszystkich klatkach cyklu, dodając lub odejmując go od wartości xij. Poprzednie wartości xij skreślamy, a nowe wartości x33 = 0, x21 = 5, x11 = 0 i x13 = 5 wpisujemy obok
6. Budujemy nową tablicę
ai |
5 |
10 |
20 |
15 |
|
1 |
9 |
4 |
3 |
|
⊖ . |
|
⊕ 5 |
⊖ 5 |
|
4 |
1 |
6 |
7 |
|
⊕ 5 |
⊖ 10 |
|
|
|
8 |
3 |
5 |
2 |
|
|
⊕ . |
⊖ 15 |
⊕ 10 |
3. Najdłuższym czasem dostawy jest t33 = 5. Wykreślamy z tablicy klatki zawierające czasy dłuższe - jest to klatka z t23 = 6). Klatkę [3,3] oznaczamy znakiem „-”.
4. Spróbujmy rozładować klatkę [3,3]. Można dla niej zbudować dwa cykle: [3,3] [3,2] [2,2] [2,1] [1,1] [1,3] [3,3] oraz [3,3] [3,4] [1,4] [1,3] [3,3]. Niestety nie są one cyklami rozładowującymi:
- najmniejszą wartością przydziału w półłańcuchu ujemnym pierwszego cyklu byłby przydział x32 = 0, a przenoszenie zera nie zmienia rozwiązania,
- najmniejszą wartością przydziału w półłańcuchu ujemnym drugiego cyklu byłby przydział x14 = 5, a przeniesienie tej wartości tylko zmniejszy przydział rozładowywany przydział do x33 = 10,
co oznacza, że aktualne rozwiązanie jest optymalne.
Najkrótszym możliwym czasem dostawy jest 5 jednostek czasu. Dla porównania, najkrótszy możliwy czas dostawy dla pierwszego przydziału wynosił 6 jednostek czasu.
Problem przydziału
Czasem przed kierownictwem eksploatacji stoi problem optymalnego przydziału lub przyporządkowania:
pracowników do pracy na różnych stanowiskach obsługowych lub naprawczych, gdy znane są wydajności ich pracy na tych stanowiskach
operatorów do sterowania danymi typami maszyn w systemie użytkowania (operacyjnym systemu eksploatacji), jeżeli znana jest miara ich przydatności do sterowania tymi maszynami
wykonawców do wykonywania określonych zadań, gdy znana jest miara ich przydatności do tych zadań
usługodawców zewnętrznych do zrealizowania kilku usług, gdy znane są miary opłacalności korzystania z różnych usług tych usługodawców
Problem ten może być rozwiązany metodami matematycznymi opracowanymi dla zagadnień transportowych. Warunkiem optymalizacji przyporządkowania jest uzyskanie maksymalnej lub minimalnej wartości pewnego kryterium globalnego.
Formalnie problem przydziału można sprowadzić do zagadnienia transportowego, w którym wielkość zapasów w każdym magazynie jest równa 1, zapotrzebowanie każdego odbiorcy jest także równe 1, a zmienne decyzyjne mogą przyjmować tylko dwie wartości:
- xij = 1 - oznacza, że dokonano przydziału elementu i do zadania j;
- xij = 0 - oznacza, że elementu i nie przydzielono do wykonania zadania j.
Może być poszukiwane maksimum lub minimum funkcji celu oraz należy zwrócić uwagę, że sens fizyczny macierzy C = [cij]m x n jest zależny od rodzaju danego zagadnienia.
Sformułowanie problemu przydziału jest więc następujące: znaleźć macierz zmiennych decyzyjnych X = [xij]m×n, która optymalizuje formę liniową ![]()
dla kryterium kosztów lub ![]()
dla kryterium czasu przy danych ograniczeniach ![]()
, ![]()
oraz ![]()
Metoda rozwiązania problemu przydziału jest identyczna jak zagadnienia transportowego z kryterium kosztów gdy poszukuje się najtańszego rozwiązania oraz z kryterium kosztów gdy poszukuje się najszybszego rozwiązania.
Obowiązuje także warunek równości podaży i popytu, który wymusza równość liczby dostawców m i liczby odbiorców n. Dla zagadnienia transportowego z kryterium kosztów daje to też m przydziałów równych 1 i m - 1 przydziałów równych zeru wybranemu, aby operować m + n + 1 równaniami przy wyznaczaniu ciągów R i S potrzebnych do przekształceń ekwiwalentnych macierzy kosztów.
W przypadku, gdy poszukujemy maksimum funkcji kryterium należy skorzystać ze znanej zależności max Z = - min (-Z) i w tabeli wpisać elementy macierzy kosztów ze zmienionymi znakami.
cykl: [1,1] [1,3] [5,3] [5,5] [3,5] [3,1] [1,1]
półłańcuch dodatni: [1,1] [5,3] [3,5]
półłańcuch ujemny: [1,3] [5,5] [3,1]
Wyszukiwarka