METODY BADANIA PIONOWOŚCI BUDOWLI WYSMUKŁYCH.

1-trygonometryczna

2-bezpośredniego rzutowania

3-wcięć

4-jednego punktu oporowego

5-projekcji laserowej

1) polega na wyznaczeniu wychyleń kątowych poszczególnych p-tów budowli w stos. do p-tu na najniż. poziomie. Pomiary z 3 stanow. symetrycznie wokół budowli. Odl. stanow. od bud. >1,5 h.

składowe wychylenia ze stanowisk:

wektory r1, r2, r3 są prostopadłe do kier. celowania ze stanow. 1, 2, 3. Wielkość wychylenia R i jego rzuty Rx i Ry obl, się ze wzorów:

α1,α2,α3 azymuty linii celowania azymut i wielkość wychylenia wylicza się ze wzoru:

błąd wychylenia wypadkowego:

wartość przybliżona bł. azymutu wychylenia wypadkowego:

Mając 3 składowe wychylenia r1, r2, r3 można wyznaczyć wychylenie wypadkowe met. analit.-graf. Langa. Szkicujemy rozmieszczenie stanow i nanosimy kierunki celu na najnizszy poziom. Od tych kierunków odkłada się wielkości r wyznaczone na i-tym poziomie. Przez końce takich odcinków prowadzimy proste równoległe do kierunków średnich. Proste tworzą trójkąt błędów. Geometrycny środek trójk. bł. określa położenie osi komina na danym poziomie. Wymiary trojk. błędów zależą od bł. pomiaru.

Budowle wysmukłe to bud. których wys. kilkakrotnie przewyższa szerokość. kominy przemysłowe, chłodnie kominowe, wieże, maszty telewizyjne, latarnie itp. Geod. obsł obejmuje:

-projekt realizacji prac geodezyjnyc

-założenie geod. sieci realizacyjnyc

-wykonanie prac realizacyjnych

-kontrola w trakcie wznoszenia

-inwentaryz. powykon. i sporządze-nie dokumentacji powykonawczej

-obserwacja odkształceń w czasie montażu

Budowle wysm. mierzy się też w okresie eksploatacji. W celu wy-krycia odchyleń od pionowego i prostoliniowego przebiegu osi bu-dowli prowadzi się pomiary pio-nowości. Wykorzystuje się kilka metod.

OBL. MAS ZIEMNYCH

Met. siatki kwadratów

Projektowana płaszczyzna dzieli obszar działki na części znajdujące się pod i nad tą płaszczyzną - inaczej na obszary wykopów i nasypów. Linia przecięcia powierzchni terenu z pow. projektowaną nazywa się linią robót zerowych. Na podst. rzędnych istniejących i projektowanych, otrzymujemy objętość danego wykopu lub nasypu.

Pow. nasypu i wykopu określa się analitycznie, graficznie lub mechanicznie. Błąd wyznaczenia zależy przede wszystkim od długości boku kwadratu

dokładność ze wzoru Gauss-a: m_V²=(Vm_S/S)²+(S/3)²3m_h²+m_Vu²

Met. przekrojów poprzecznych

Sposób ten jest powszechnie stosowany do obliczania robót ziemnych przy projektowaniu „budowli” o kształcie wydłużonym.

wzór ścisły na obliczenie objętości

1. V = d/3 (F₁ + F₂ + √(F₁F₂))

2. wzór Simpsona

V = d/6 (F₁ + F₂ + 4F_ŚR)

3. wzór Czepsena

V = d/2(F₁+F₂) - d/6 i (h₂-h₁)

i - spadek terenu

F₁, F₂ - pola powierzchni przekrojów poprzecznych;

d - odległość między przekrojami

DROGA

Przy projektowaniu wykorzystuje się mapy syt-wys gdzie nanosi się wszystkie elementy projektowanej trasy. Projekt wykonuje się w pł. poziomej i pion.

1)wykonanie projektu na mapie

2)tyczenie w terenie p-ktu początkowego i końcowego odcinka trasy oraz p-któw wierzchołkowych

3)pomiar długości odcinków kierunków głównych oraz kątów zwrotu stycznych

4)na podst. parametrów określonych projektem obliczamy miary liniowe i kątowe i wyznaczamy p-kty gł. i pośrednie, sporządzamy szkice realizacyjne

5)wyzn. kilometraż wszystkich p-któw trasy

6)projektujemy niweletę i obl. łuki pion., wykonujemy przekr. poprz.

P-kty główne to p-kty styku łuku kołowego z prostymi głównymi trasy. Wyznaczenie terenowe polega na odłożeniu miar kątowych i liniowych od p-ktu wierzchołkowego (wyzn. na podst. osn. geod.) i kierunków głównych. W celu kontroli prawidłowości wyznaczenia wyznaczać p-kt środkowy S na 2 sposoby. Styczna główna t - dł. od W do P lub K. t = R tg (α/2); WS = R (secα/2 - 1)

W celu bezpieczeństwa między prostą i łukiem stosuje się krzywą przejściową o zmiennej krzywiźnie. Jest to klotoida o parametrze a

LR = a² = const. Łagodzi ona działanie siły odśrodkow. Stosowane są 2 klotoidy symetryczne (jednakowe a) lub niesymetryczne (różne a). P-kty gł. klotoidy to p-kty styczności z prostą i łukiem kołowym. Wzory (łuk kołowy z klotoidami)

 = L/2R = L²/2a²  = γ-2

Xs = X-Rsin ; H = Y-R(1-cos );

Ys = R+H = Y+Rcos ;

T = X+Ytg ; T_D = X-Yctg ;

T_D = X-Yctg ; N = Y/cos ;

T_s = (R+H) tg γ/2; T_o = T_s+X_s;

Z = (R+H)(secγ/2 - 1)+H;

Z' = R(secα/2 - 1); patrz rysunek

Łuk koszowy - zespół krzywych (2 lub więcej łuków kołowych) o różnych prom.; mają 1,2 lub więcej p-któw wspólnych i wspólne styczne w tych p-ktach. P-kty gł. łuku koszowego to p-kty styczności z prostymi gł. i p-kty wspólne poszczególnych łuków. Wyznacza się je tak samo jak pojedynczy łuk kołowy.

α = α₁ + α₂;

t₂ = t₁cosβ+R₁sinβ-(R₁-R₂)sinα₂

R₂ = t₁sinβ-R₁cosβ-(R₁-R₂)cosα₂

cosα₂=(t₁sinβ-R₁cosβ-R₂)/(R₁-R₂)

α₁ = (200^g - β) - α₂

PM₁=M₁S₁=S₁N₁=N₁T₁=R₁tgα₁/4

TYCZENIE P-KTÓW POŚREDN.

met. rzędnych od stycznej dla równych odcinków łuku

p-kty na łuku tyczy się w równych odstępach Δl. Dla tej wartości wyznacza kąt środkowy Δα i wartości x i y poszczególnych p-któw pośrednich.

x_i=Rsin(i_*Δα); y_i = R[1-cos(i_*Δα)]

Δα^g = Δl _* ρ^g / R

met. rzędnych od stycznej dla równych odcinków na stycznej

zakłada się równe odcinki na stycznej (jednakowe wartości x), wyznacza się kolejne y.

y = R-√(R₂-x₂) lub y ≈ x² / 2R

met. biegunowa w tyczeniu p-któw pośr. łuku kołowego

Podobnie jak przy tyczeniu klotoidy. Od stycznej KKP-W odkłada się kolejne wartości kąta biegunowego i w ten sposób (znając od-ległość do kolejnych p-któw pośr.) otrzymujemy szukane p-kty. Rysunek podobny do poniższego, tyle że między p-ktami pośr. jest jeszcze cięciwa c. Δα=(Δl/r)_*ρ d_i = 2Rsin(i_* (Δα/2))

c = 2R sin(Δα/2)

met. od przedłużonej cięciwy w łuku kołowym

łuk dzieli się na równe odcinki, od stycznej gł. odkłada się wart. x i prostopadle y. Później od cięciwy P-1 tak samo i mamy p-kt 2. Cięciwa 1-2, odkł. x i y - mamy p-kt 3 itd. Istnieje jednak możliwość wystąpienia błędów wytyczenia (przenoszenie błędów - źle wyznaczony p-kt wpływa na kolejne p-kty).

ϕ=(Δl/2R)_*ρ; x₁=ccosϕ; x₂=ccos2ϕ

c=2Rsinϕ, y₁=csinϕ; y₂=csin2ϕ

met. rzędnych od cięciwy przy p-ktach pośr. łuku kołowego

Na cięciwie odkłada się wart. x a na prostopadłej wart. y. Wielkości wyznacza się pośrednio na podst. obliczonych a, s, x oraz y. x i y wyznacza się identycznie jak met. rzędnych od stycznej dla równych odcinków łuku.

a = Rsinα/2; s = R(1-cosα/2); Δα = (Δl/R)ρ;

x_i' = Rsin(i Δα); y_i' = R[1-cos(iΔα)] x = a - x'; y = s - y'

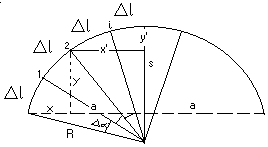
TYCZENIE P-KTÓW POŚREDN. KLOTOIDY

Met. rzędnych od stycznej

wartości rzędnych i odciętych oblicza się w odniesieniu do klotoidy jednostkowej a=1, później przelicza się wg wzoru

x=L - L⁵/40 + ...; y=L³/6-L⁷/336 +...

X = a x oraz Y = a y

Met. biegunowa

określamy wartości odpowiednich kątów i długości, które później realizujemy w terenie.

x =L - L⁵/40 + ...; y =L³/6-L⁷/336 +...
ω =arc tg y/x; d =a√(x²+y²)

OPRACOWANIE PIONOWE DROGI

Przekrój podłużny wykonuje się na podst. niwelacji trasy lub na podst. aktualnej mapy syt.-wys. Na przekrój terenu wkreśla się niweletę.

Załamania niwelety w płaszcz. pionowej powinny być złagodzone przez zastosowanie łuków pionowych (wklęsłych lub wypukłych). Tyczenie jak w łuku poziomym - p-kty gł. i pośr.

Spadek niwelety i₁=ΔH₁/D_{1 *} 100% oraz i₂=ΔH₂/D_{2 *} 100%

styczna t do łuku pion. t = R/2 (i₁+i₂); WS = t²/2R

P-kty pośr. wyznaczono ze wzoru: y_i ≈ x_i² / 2R

Obliczenie rzędnych ze wzorów

dla niwelety „pod górkę” H = H_P + i_{1 *} x

dla niwelety „z górki” H = H_k - i_{2 *} x

x - odl. danego p-ktu od początku (lub końca) łuku. Należy też wykonać przekroje poprz. Są tam rzędne niwelety, korony drogi, szer. jezdni, pasa drogowego, głęb. rowów, itd. Wykonuje się je dla p-któw charakterystycznych: p-kty gł., załamania niwelety, p-kty hektometrowe, skrzyżowania, p-kty zmian wys. jezdni...

PRZENIESIENIE WYSOKOŚCI PRZEZ PRZESZKODY WODNE

Przy budowie mostów, zapór itp. zachodzi potrzeba przeniesienia wysokości przez przeszkody wodne. Stosuje się met. niwelacji geo-metrycznej lub trygonometrycznej przy użyciu tarcz bisekcyjnych.

Met. niwelacji geometrycznej

Na łacie A wykonuje się odczyt wstecz, następnie (przy spoziomowanej osi celowej) celujemy na łatę na reperze B. Pomiarowy przesuwa tarczę bisekcyjną do momentu pokrycia poziomej kreski krzyża i środka tarczy. Należy wykonać kilka serii pomiarów by wyeliminować błędy. Z różnicy odczytów A i B otrzymuje się różnicę wysokości.

Met. niwelacji trygonometrycznej

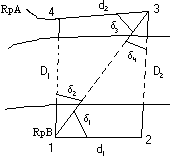
zasada przedstawiona jest na rysunku.

Przewyższenie ΔH można obliczyć trzykrotnie na podst. kątów α, β, γ. Chcąc zwiększyć dokładność wyznacz. ΔH należy przeprowadzić obserwacje jednocześnie z dwóch stanowisk po obu brzegach przeszkody.

Na p-ktach 2 i 4 ustawia się statywy z tarczami bisekcyjnymi i mierzy się wysokości tarcz nad p-ktami oraz między tarczami. Teodolity ustawia się na p-ktach 1 i 3. Obserwacje kątów pionowych wykonuje się jednocześnie. Mierzy się również kąty poziome.

Dokł. określenia różnicy wys. tą met. oblicza się ze wzoru:

m_h=√[(tgα+(1-K/r)D₀)m_do]²+(d_om/cos²α)² + (d_om_K/2r)²

α - kąt pionowy

K - współczynnik refrakcji

r - promień kuli ziemskiej

d_o - odległość między p-ktami

Na błąd przyrostu wysokości największy wpływ ma błąd pomiaru kąta pionowego, wpływ odległości nie ma większego znaczenia.

ΔH = i_t +Dtgα - i_s + D²[(1-K)/2r]

PROJEKTOWANIE PŁASZCZYZN BILANSUJĄCYCH

ROBOTY ZIEMNE

Każda płaszczyzna przechodząca przez środek ciężkości jest płaszczyzną bilansującą roboty ziemne.

1) średnia wartość współrzędnych

X_S=Σ x_i/n Y_S=Σ y_i/n Z_S=Σ z_i/n

2) jeżeli pł. bilansująca ma zadany kierunek najw. spadku α i wart. najw. spadku k to równanie płaszcz. to:

(kcosα)x + (ksinα)y - z + H_o = 0

H_o = - X_Skcosα - Y_Sksinα + Z_S

3) jeżeli projektowana płaszcz. ma przechodzić przez 2 p-kty

1=(x1, y1, z1) i 2=(x2, y2, z2) to

(x₁-X_S)kcosα + (y₁-Y_S)ksinα - (z₁-Z_S) =0

(x₂-X_S)kcosα + (y₂-Y_S)ksinα - (z₂-Z_S) =0

kcosα i ksinα dają tgα i liczymy α

4) jeżeli projektowana płaszcz. ma przechodzić przez 1 dany p-kt i ma określony max spadek wzdłuż kierunku α to mamy jedno r-nie;

(x₁-X_S)kcosα + (y₁-Y_S)ksinα - (z₁-Z_S) =0

5) jeżeli projektowana płaszcz. ma przechodzić przez 1 dany p-kt i ma określony max spadek k to mamy jedno r-nie;

(x₁-X_S)kcosα + (y₁-Y_S)ksinα - (z₁-Z_S) =0

dołączamy równanie sin²α+cos²α=1 i wyliczamy α

Projektowanie płaszcz. minimalizujących roboty ziemne

a) dla każdego p-ktu o znanych wsp. zestawiamy r-nie

v_i = (x₁-X_S)kcosα + (y₁-Y_S)ksinα - (z₁-Z_S)

r-nie te wagujemy proporcjonalnie do powierzchni otaczającej dany p-kt i rozwiązujemy wg [pvv] = min

b) projektowana płaszcz, ma zminimalizować roboty ziemne i zbilansować je. Wtedy dla każdego p-ktu o znanych X i Y zestawiamy następujące r-nie aproksymujące:

v_i = e_X x_i + e_y y_i + z₀ - z_i

e_X - nachylenie pł. wzdłuż osi OX

e_y - nachylenie pł. wzdłuż osi OY

z₀ - przecięcie pł. z osią OZ

Metoda przekrojów poziomych z mapy warstwicowej

V = h/2 Σ(S_i+S_i+1) + Δh/3_*S_n

Met. siatki trójkątów

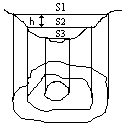
V = a²/2 _* 1/3(h₁+h₂+h₃)

Met. p-tów rozproszonych

V = 1/3 S₁(h₁+h₂+h₃)

m_V²=(Vm_S/S)²+(S/3)²3m_h²+m_Vu²

m_Vu² = 0,6 Q S√b

Q - współczynnik bogactwa mikro-rzeźby (0,005 - 0,01)

b - średnia długość celowej

Na dokł określenia objętości składają się następujące błędy:

m_K - bł. ukształt. pow. terenu

m_g - bł. zagęszczenia gruntów

m_W - wpływ dokł. materiałów wyjściowych.

m_K - bł. ukształt. pow. terenu

ε = R - x; x = √(R²-a²/4)

Błąd obliczonej objętości ze wzgl. na ukształtowanie terenu wynosi

m_Vu² = S ε_SR = n a² ε_SR

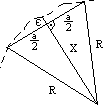
Wpływ błędu zagęszczenia terenu

D=V_W/W_N; V_W=V_N D ±0,02D V_N

0,02D - ustalona tolerancja stopnia zagęszczenia gruntu; wg Polskiej Normy 0,9<D<1,15

Wpływ dokładności materiałów wyjściowych

można to sprowadzić do wpływu dokładności wyznaczenia rzędnych terenu h.

1) V = S h₀ 2) V = ΣS_i 1/KΣh_J

3) h₀ = V/S 4) h_J = h_J' ± m_hJ + u_J

Jeżeli do r-nia 3 podstawimy r-nie 4 to otrzymamy:

m_Vh = ±m₀√(S/K) + u₀S

u0 - bł. systemat. rzędnej wysokośc

m0 - bł. jednoznacznego określ. h

0,02m - niw. siatk.

0,10m - tachimetria

0,05m - p-ty rozproszone

0,05m - niw. przekrojów

0,20m - aerofotogrametria

TORY KOLEJOWE

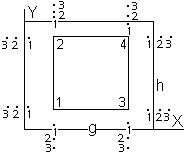
Jedno-, dwu- i wielotorowe. Rozjazdy są zwyczajne i krzyżowe. Rozjazd zwyczajny składa się ze zwrotnicy, torów łączących (wygiętych wg promienia łuku kołowego), krzyżownicy. Typ rozjazdu podaje się symbolem, np. S49-300-1:9. S49- typ szyny, 300-promień toru odgałęźnego, 1:9-skos rozjazdu. Gdy od toru głównego odgałęziają się 2 tory w tę samą lub różne strony należy między początkami rozjazdów zaprojektować wstawkę prostej.

Projekt linii kolejowej obejmuje określenie niezbędnych miar kątowych i liniowych oraz sporządzenie szkiców umożliwiających terenową realizację projektu technicznego. W proj. tech. określa się parametry techniczne linii kolejowej.

Połączenie torów równoległych rozjazdami o równych skosach

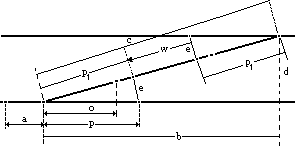
Wytyczenie polega na określeniu w terenie poł. p-któw środkowych poszczególnych rozjazdów oraz p-któw pocz. i końcowych. Położ. p-ktu środk. wyznacza się w stosunku do istniejących torów lub osn. geod. i do założonego kilometrażu tego p-ktu. Pozostałe p-kty wyznacza się przez odłożenie odpowiednich miar.

Połączenie torów równoległych rozjazdami o różnych skosach

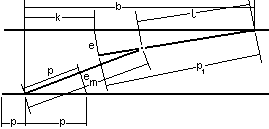
Opracowanie geo. sprowadza się do określenia położenia p-któw głównych poszczególnych rozjazdów. Punktem wyjściowym jest środek rozjazdu krzyżowego.

Połączenie dwóch torów równoległych

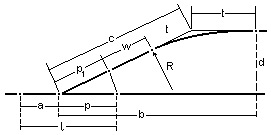
Opracowanie geo, polega na określeniu położenia p-któw głównych rozjazdu, wstawki prostej w oraz p-któw gł. łuku kołowego w torze odgałęźnym. Minimalną wartość wstawki proste „w” oblicza się ze wzoru: w_min = V/6

V - max. prędkość taboru założona w projekcie

c = √(b²+d²) - miara kontrolna

d - rozstaw torów ; b = nd

t_proj = c-(p₁ + w_min) ; t_prakt = R tg α/2 ; w_prakt = c - (p₁ + t_prakt)

Osnowę podst. linii kolejowych stanowi osn. państwowa I i II kl. Sieć ta jest dostatecznie gęsta by nie zachodziła potrzeba zakładania odrębnej osnowy podst. dla terenów kolejowych. Osnowę szczegół. do celów inwentaryzacji stanowi sieć p-któw osn. państw. III i IV kl. Ze wzgl. na kształt szlaków kolejowych najwłaściwszą metodą zakładania osnów jest met. poligonowa. Ciągi kl. III powinny być nawiązane bezpośrednio do osn. I lub II kl., powinny znajdować się w granicach pasa wywłaszczenia, w pobliżu osi linii kolejowej. Ciągi powinny być zbliżone do prostoliniowych, dł. nie powinna przekraczać 3 km, dł. boku 100-300 m. dokł. pomiaru boku 1:5000, kąta ±10″

Osn. IV kl. - ciągi sytuacyjne lub linie pomiarowe, nawiązane do III kl. Dł. ciągu <2 km, linii pomiarowych 400m. Dł. boku ciągu sytuacyjnego 50-350m, stosunek 2 sąsiednich boków >1:3. Bł. pom. bo-ku 1:5000, kąta ±20″.

SUWNICE

Wymagania techniczne szyn torów podsuwnicowych:

-prostoliniowe i równoległe;

-równooddalone (wg zał. projektu)

-we właściwej odl. od elementów konstrukcji hali czy estakady

-ułożone poziomo na jednej wysokości

Szyny suwnic układa się na belkach stalowych lub żelbetowych, te zaś oparte są na słupach nośnych lub wspornikach wystających ze słupów nośnych konstrukcji hali.

1) różnica poziomów główek szyn

± 10mm na podporach

± 15mm w przęśle

2) różnica poziomów główek w tej samej osi podłużnej b/1500 <10mm

3) max odchyłka w prześwicie ± 5mm (odch. od projektu)

4) odch. osi teoretycznej szyny od rzeczywistej ± 2,5mm

5) odchylenie czoła szyn w styku w pionie i poziomie max ± 1mm

6) max przerwa na łączeniu obu szyn ± 4mm

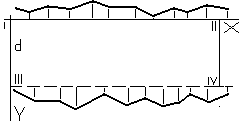
W terenie stabilizujemy 4 stanowiska osnowy kontrolnej. Wyznaczamy wsp. stanowisk, później rzędne p-któw zasygnalizowanych na belkach od płaszczyzn pionowych I-II i III-IV.

Do pomiaru stosuje się łatę układaną poziomo i prostopadle do belek, tak by jej początek pokrywał się z oznaczonymi punktami ich osi. Na podst. danych z pomiaru określa się odchyłki osi belek od projektowanych osi szyn. Oblicza się je w taki sposób, by jednocześnie uzyskać dane do wyznaczenia wskaźników montażowych szyn toru suwnicowego. Wskaźniki te powinny leżeć na dwóch prostych równoległych i odległych o projektowany rozstaw szyn. Należy je wpasować w teoretyczne osie. Przy wpasowaniu stosuje się met. spełniająca warunek minimum sumy kwadratów odchyłek osi belek od ich osi projektowanych. Opracowanie wykonuje się dwiema metodami:

- analityczno - graficzna

- analityczna

Analityczno - graficzna

Mając odczyty z łaty L i P obliczamy y_L i y_P praktyczne w układzie odniesienia (geodezyjnym). Obliczamy środek toru dla każdego zasygnalizowanego p-ktu [y₀=(y_L+y_P)/2] i wartość średnią położenia osi toru [y_śr=(ΣY₀)/n]. Następnie obl. odchyłki ze wzoru: y₀-y_śr. Obliczone odchyłki odejmujemy od teoretycznej wartości położenia osi toru (Y₀), po czym obliczamy Y_L=Y₀-S/2 i Y_P=Y₀+S/2. W końcu wyliczamy odchyłki osi belek w oznaczonych p-ktach od wypośrodkowanych osi teoretycznych: V_YL=y_L-Y_L; V_YP=y_P-Y_P oraz odchyłki rozstawu osi belek w poszczególnych przekrojach V_ROZ=V_YP-V_YL

Met. analityczna

Różni się od anal-graf, że nie rysujemy wypośrodkowanej osi toru, ale obliczamy współczynniki tej osi oraz współrzędne Y0 przez podstawienie ich do odpowiednich równań poprawek. Równania układa się wg wzoru: a_*i+b = y₀-y_śr+v; i = d_i/d

a,b -współczynniki równania osi toru

di - odl p-ktu od początku toru

d - odl. między sąsiednimi p-ktami

y₀-y_śr - wyraz wolny równania

v - poprawka

Obliczone odchyłki p-któw oznaczonych na osiach belek od wypośrodkowanych teoretycz. osi szyn wykorzystywane są w ten sposób, że odkłada się je od wspomnianych p-któw z odwrotnym znakiem, uzyskując na belkach miejsca wskaźników do montażu szyn.

SZYBY DŹWIGOWE

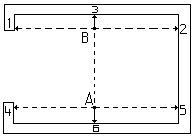
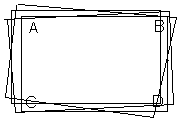
Jednocześnie z pomiarem kontrolnym po montażu ścian każdej kondygnacji należy wykonać pomiar kontrolny zmontowanych szybów dźwigowych. Wyniki tego pomiaru przedstawia się na jednym szkicu z wynikami pomiaru ścian, by przed montażem następnej kondygnacji można było wykonać korektę w dalszym montażu. Po wykonaniu stanu surowego budynku wykonuje się pomiar odchyłek ścian szybów dźwigowych przed montażem dźwigów. Celem jest stwierdzenie zachowania dopuszczalnych odchyłek szybów oraz uzyskanie danych do osadzenia prowadnic dźwigowych. Dla szybów montowanych z prefabrykatów wykonuje się najczęściej pomiar pionowości i rozstawów ścian z osnowy, którą stanowi zakładana na górze lub dole dwupunktowa baza AB.

W p-ktach A i B ustawia się pion opt. i 2-krotnie odczytuje na łacie odległości od pionowej osi celowej do ścian szybu. Odczyty wykonuje się dla p-któw 1-6 na każdym poziomie roboczym. Dla każdego przekroju oblicza się różnice między odczytami na poszczególnych kondygnacjach a następnie śr. arytmet. wszystkich odczytów (dopasowaną do wymiarów projektowych szybu).

Wpasowanie osi prowadnic dźwigowych i optymalizacja wpasowania

Czynność polega na znalezieniu max prostopadłościanu, który da się wpasować w przestrzeń ograniczoną ścianami szybu. Wpasowanie wykonuje się met. graficzną lub analityczną.

Petoda graficzna

Osnową są 4 p-kty wierzchołkowe prostokąta o znanych współrz. Wszystkie przekroje orientuje się względem prostokąta i nanosi na jeden rysunek. Na kalkę nanosi się osie prowadnic i wpasowuje się w rys. przekrojów.

Pet. analityczna

Określa się optymalne płaszcz. w których montuje się prowadnice. Podst. opracowania jest met. parametr. z warunkami wiążącymi niewiadome. Obliczenia wykonuje się w ukł., gdzie osiami XY są krawędzie ścian szybu w piwnicy budynku. W stosunku do tych osi odnosi się krawędzie ścian dla każdej kondygnacji.

Kolejność obliczeń;

1) obl x i y p-któw obserwowanych

2) ułożenie równań poprawek

X_i^obs + V_X = X_i^wyr

Y_i^obs + V_Y = Y_i^wyr

3) nałożenie na niewiadome warunku równoległości i prostopadłości:

war. równoległości war. prostopadłości

X₃^W - X₁^W = g X₂^W - X₁^W = 0

X₄^W - X₂^W = g X₄^W - X₃^W = 0

Y₂^W - Y₁^W = h Y₄^W - Y₂^W = 0

Y₄^W - Y₃^W = h Y₃^W - Y₁^W = 0

Optymalizacja to ponowny pomiar poprawności wykonania pionem optycznym (bo montażyści używają ciężkich pionów sznurkowych)

PRZENOSZENIE WSKAŹNIKÓW KONSTRUKCYJNYCH

Przed przystąpieniem do obsługi geod. kondygnacji powtarzalnych i wyznacz. wskaźników konstrukcyjnych na poszczegól. poziomach robocz. należy sporządzić szkic tyczenia, zawierający rozmieszcz. osi konstrukcyjnych zgodnie ze szkicem dokumentacyjnym oraz osnowę budowl.-montaż. Osn. ta będzie służyć do przenoszenia osi konstrukcyjnych na poszczególne kondygnacje.

Met. stałej prostej

a) stawiamy teodol. na p-kcie linii bazowej osnowy bud-mont., celujemy na tarczę na końcu tej linii

b) poziomujemy teodol. przy każ-dym pomiarze

c) układamy łatę na stropie kondygnacji roboczej i ustawiamy ją prostopadle do płaszcz. celowania

d) łatę ustawiamy tak, by obraz tarczy sygn. znalazł się na pionowej kresce siatki celowniczej teodol.

e) zaznaczamy na stropie tyczony punkt. Czynności w 2 poł. lunety.

1) jeśli O_K=O_P to O_K'-ΔK = O_P'-ΔP

2) ΔK = d_K/d_{P *} ΔP O_K'-O_P' = (d_K/d_{P *} ΔP) - ΔP

O_K'-O_P' = (d_K/d_P -1) _* ΔP O_K'-O_P' = [(d_K-d_p)/d_P] _* ΔP

poprawki trasowania

ΔP = [(O_K'-O_P')/(d_K-d_P)] _* d_P

ΔK = [O_K'-O_P'] + ΔP

analiza dokładności

1.bł centrowania teodol. 0,4mm

2.bł centrowania sygnału 0,4mm

3.niepionowość osi obrotu teodol. 0,9mm

4.bł celowania na tarczę 0,3mm

5.bł wprowadzenia sygn. w oś celową 0,4mm

6.bł oznaczania wskaźnika 0,8mm

7.inne błędy 0,3mm

m = √(m₁₂+m₂²+...m₇²) = ± 1,4mm

Metoda rzutowania

Wyznacza się osie konstrukcyjne lub linie równoległe do tych osi dla ścian zewn. i wewn. Przenosi się też tą met. wszystkie typy osnowy wewn. na kondygnację roboczą.

1) teod. stawiamy na stanow., poziomujemy, celujemy pionową kreską na wskaźnik wyjściowy na bud.

2) w 2 poł. lunety wyznaczamy wskaźnik na krawędzi stropu wg kreski pion.

3) każdorazowo poziomujemy teod.

4) analogicznie wyzn. wskaźnik z drugiej strony budynku

5) wtyczyć teod. w linię przeniesionych wskaźników i za pomocą łaty realizacyjnej wyznaczamy wskaźniki ścian zewn.

ANALIZA:

niepionowość osi obrotu teod. 0,9mm

bł. celowania 0,3mm

bł. wprowadzenia sygnału w płaszcz. rzutowania 0,4mm

oznacz. wskaźnika na stropie 0,8mm

m² = m₁²+...m₄² = 1,3mm

Metoda biegunowa

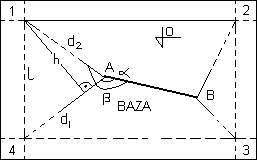
l² = d₁² + d₂² - 2d₁d₂cos(β-α)

m_L² = cos²αm_d1² + cos²αm_d2² + h²m_β² + h²m_α²

ANALIZA

bł centrowania pionownika 0,3mm

bł poziomowania libelli 0,1mm

bł odczytu podziałki 0,7mm

bł oznaczenia p-ktu na tarczy 0,5mm

m = 0,5mm przy n kondygnacjach m_n = 0,5√n

TYCZENIE DŁUGICH PROS-TYCH PRZEZ PRZESZKODY

1.Odcinek do 2km tyczymy przy pomocy teodolitu. Na końcu odcinka stawiamy sygn. Tyczymy od p-ktu najdalszego do najbliższego. P-kty w odl. <=300m

2.Odcinki do 5km tyczymy etapami jak w met.1. Wyznaczamy p-kt najdalszy i pośrednie na tej linii, potem przenosimy teodolit na ten najdalszy p-kt i powtarzamy czynność.

3.Mniej - więcej w pobliżu środka prostej wybieramy p-kt, mierzymy na nim kąt wierzchołkowy i obliczamy przesunięcie d, które należy wykonać, by p-kt znalazł się dokładnie na tyczonej prostej.

4.Proste dłuższe od 5km - tyczenie etapami (2) lub punktami posiłkowymi (3).

Tyczenie w terenie falistym

1.Jeśli z p-ktu pocz. widać końcowy to tyczymy najdalszy p-kt pomocniczy. Jeśli z dalekiego p-ktu pomocniczego nie widać końcowego to stosujemy met. przedłużeń (na najdalszym stawiamy teodolit, celujemy na p-kt pocz. przechylamy przez ze-nit i wyznaczamy p-kt najdalszy lub końcowy. Robimy to 2-krotnie).

2.Jeżeli nie widać p-ktu końcowego, a istnieje osnowa geod., to po nawiązaniu do niej kierunku trasy obliczymy wsp. p-ktu począt i koń

3.Jeśli nie widać p-ktu P i K, ale w pobliżu w terenie istnieje sieć poligonowa, to p-kty kierunkowe można wyznaczyć przez oblicz. przecięć prostej PK z bokami poligonowymi albo przez obliczenie domiarów prostokątnych lub biegunowych do określonych p-któw.

Tyczenie przez przeszkody

1.Obywa się w sposób pośredni. Jeśli p-kty P i K są wzajemnie niewidoczne to obok przeszkody wyznaczamy linię pomocniczą PL i mierzymy odc. KL i kąt α na stanowisku L. Później z zależności matematycznych wyznaczamy p-kty pośrednie linii PK.

2.Jeżeli przeszkoda rozciąga się na dużej przestrzeni (np. las) i celowanie z P na K jest niemożliwe to kierunek prostej tyczy się w przybliżeniu przez wyznaczenie azymutu PK i tyczenie go w terenie za p-mocą busoli. Sposób jest dobry gdy PK<1200m.

Dokładne wytyczenie trasy można wykonać po założeniu specjalnej osnowy wokół przeszkody. Dla krótszych odcinków może to być osnowa poligonowa, dla długich - specjalna sieć triangulacyjna.

PLAN REALIZACYJNY

część opisowa to: przedmiot i zakres inwestycji; opis istniejącego zagospodarowania terenu; zestawienie danych o przydatności gruntów do celów budowy; infrastruktura i uzbrojenie itp. Dla celów projektowych ważne są 2 cechy podkładów mapowych: dokładność i szczegółowość. Dokładność graficzna to bł. położenia szczegółów sytuacyjnych w stosunku do poł. najbliższ. p-ktu osn. geod. I grupa dokł. 0,3mm w skali mapy; pozostałe 0,6mm. Dokł. wzajemnego poł. 2 p-któw 0,4-0,8mm w skali mapy.

Geodezyjne opracowanie planu realiz. i proj. techn.: met. graf., analit., anal-graf. 1) ustalenie lokalnego ukł. wsp. osn. realiz. i obl. wsp. 2) wyznacz. danych geod. do określenia transformacji X' Y' planu realiz. na wsp. w ukł. geod. 3) obl. XYZ p-któw określających główne elementy planu realiz. 4) obl. bł. elem. liniowych i kątowych służących do wyznacz. p-któw. 5) obl. elem. kontrolnych.

Projekt techn. obiektu budowlanego: 1) sprawdzenie danych liczbowych proj. 2) obl. p-któw gł. obiektu w ukł. planu realiz. 3) przeliczenie na ukł. geod. 4) obl. elem. geod. służących do wytyczenia obiektu w terenie. 5) wykaz geod. elem. kontrolnych. Wyniesienie proj. planu realiz. w teren: dokumentacja: zatwierdzony plan realiz. -proj. techn. obiektów budowl. -szkic dokum. -dziennik bud -szkic tyczenia -dziennik nadzoru autorskiego -warunki techn. - dokumentacja proceduralna.

Szkic dokumentacyjny: elem. osn. realiz -usytuowanie gł. i szczegółowych osi konstrukcyjnych w nawiązaniu do osn -dane wyjściowe nawiąz geod względem osn real -odl. między p-ktami osn real a osiami budowli -nr zlecenia, projektu -nazw wykonawcy, data.

Szkic tyczenia powstaje po pomiarze (zakończeniu realizacji szkicu dokumentacyjnego), nanosi się wszystko co zauważone było podczas realizacji.

Met. niwelacji trygonometrycznej

ΔH = d tgα

m_ΔH² = m_d²tg²α + (d²m_α² / β²cos⁴α)

m_α = ½ m_d/d ρ sin2αβ

Prace realizacyjne 1. geod opracowanie planu realiz oraz projektu obiektów budowl 2. tyczenie lokalizacyjne ob. budowl 3. tyczenie szczegółów 4. pomiary kontrolne 5. pomiary przemieszczeń i odkształceń podczas budowy 6. pomiary powykonawcze.

Tyczenie lokalizacyjne: określenie poł. względem osn realiz elementów projektowanego obiektu i zaznaczenie ich w terenie w taki sposób, by wytyczone p-kty mogły być wykorzystane przy wykonaniu robót bud-montażowych. Met. tyczenia lokal.: biegunowa, wcięcia kątowego w przód, ortogonalna, przecięć.

INWENTARYZACJA PRZEWODÓW PODZIEMNYCH

Bezpośrednia (przed zasypaniem) i pośrednia (pomiar rzędnej osi przewodu) tachimetrem. Dzieli się na szczegółową i zbiorczą, a oprócz tego inwent. może być schematyczna lub bramowa. Metody inwent pośredniej: 1. indukcyjna (wykorzystuje zmienne pole elektryczne oraz generator drgań i nadajnik) 2. galwaniczna (podłączenia przewodu). Met galwaniczna jest nieznacznie dokładniejsza od indukcyjnej. Wyzn poł przewodu met ind.

1. sygnał w momencie natrafienia na przewód (nadajnik wysyła fale w promieniu 5m, ciągle przesuwamy nadajnik i w ten sposób wykrywamy przewód) 2. siatka kwadratów - nadajnik na kolejnych narożnikach siatki 3. wyzn kierunku podłączenia lub załamania przewodu 4. wyzn poł przewodów leżących blisko siebie (gdy d>1m można wyzn poł, gdy d<1m - poł przybliżone).

OSNOWY REALIZACYJNE

Sytuacyjne(XY),wysokościowe(H), przestrzenne(XYH). Wszystkie dzielą się na podstawowe - szczegółowe - budowlano-montażowe. Osn. dzielą się na osn. dowolnego kształtu, regularne, układ baz, sieci wydłużone, zakładane techniką GPS.

Podst. osn. real. wiąże tyczoną inwestycję z otaczającym terenem i uzbrojeniem. Szczegół. osn. real. służy do bezpośredniego oparcia pomiarów realizacyjnych. Podst. osn. real. to pozioma osn. II kl. i wysokościowa II kl. Projektowanie to 1)czynności wstępne. 2)prace projektowe. AD.1)analiza danych wyjściowych (inform. o terenie, osnowie, plan realizacyjny inwestycji, założenia techniczne i dokładnościowe) projektu i przegląd stosowanych rozwiązań danego zadania. AD.2)projektowanie obejmuje 3 etapy analiz i ustaleń (geometria sieci i obserwacje wiążące; dokładności obserwacji; szczegóły realizacji i opracowania wyników). Do wykonania projektu sieci niezbędny jest plan realizacyjny danej inwestycji - zawiera rozmieszczenie wszystkich zaprojektowanych obiektów i urządzeń na tym terenie. Projektując sieć należy tak usytuować jej p-kty w terenie, by służyły do pomiarów przez cały okres realizacji inwestycji.

Dokładności tyczenia lokalizacyjnego

określa się na podst. dopuszczalnych odchyłek realizacji p-któw obiektów. Są to bł. tyczenia p-któw w terenie i bł. czynności budowlanych. Wartości średnich bł. tyczenia p-któw, długości lub kierunków pozwalają na określenie dokładności pomiaru sieci realizacyjnej. Tyczenie to czynności pomiarowe mające na celu wskazanie i utrwalenie w terenie lub na obiekcie zespołu p-któw o założonych z góry położeniach w stosunku do p-któw oznaczonych w terenie lub na obiekcie i przyjętych jako p-kty odniesienia. Tyczenie 2-etapowe - wytyczenie przybliżonej pozycji P° p-ktu P i po wprowadzeniu niewielkich poprawek tyczenia dX_t, dY_t ostatecznego położenia tego p-ktu.

Tyczenie 1-etapowe - wytyczenie nominalnej pozycji p-ktu P bez posługiwania się utrwaloną pozycją przybliżoną P°. Pozycję p-ktu znajdujemy przez odłożenie kątów i/lub odległości stanowiących elementy zaprojektowanej konstrukcji tyczenia.

Ogólne zasady ustalania dokładności:

m_td² = m_fd² + m²_d(α,d) lub inaczej m_td² = m₀²(F_d^T Q F_d) + m²_d(α,d)

m₀ - śr bł. jednostkowy po wyrównaniu

Q - macierz współczynników wagowych

F_d - mac. funkcyjna wiążąca dł. tyczonego odcinka ze współrz odpowiednich p-któw osnowy.

m_fd² - bł. średni wynikający z dokł. osnowy

m²_d(α,d) - bł. średni wynikający z dokładności tyczenia

m_α²=m_Ct²+m_Cs²+m_ς²+(m₀²+m_C²)/S

S - ilość serii

m_C = bł. celowania m_C=60``/G

m₀ - bł. odczytu

m_ς - bł. spowodowany niepoziomowością limbusa

m_ς = i (tgβ_P*sinδ_P - tgβ_L*sinδ_L)

i - kąt odchylenia linii największego spadku płaszczyzny limbusa od poziomu

β - kąt nachyl. osi cel do poziomu

δ - azymut osi celowej

1.ustala się jakie i ile obserwacji w sieci należy wykonać

2.ustalamy dokładn. i ilość serii pomiaru (dobór instrumentu) Analizę dokładn. można wykonać z uwzględnieniem błędów p-któw nawiązania lub bez

---