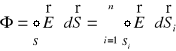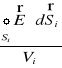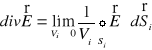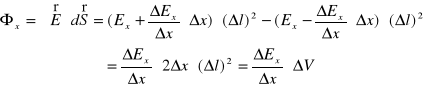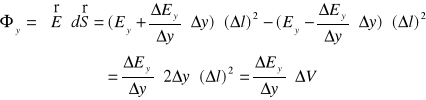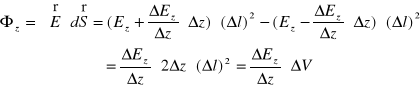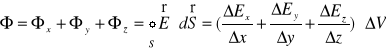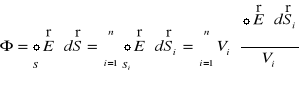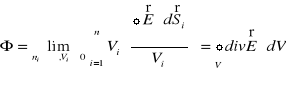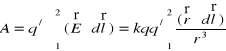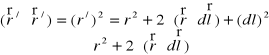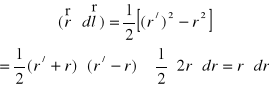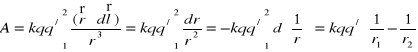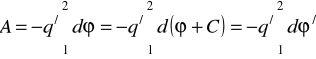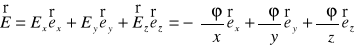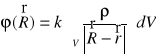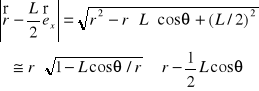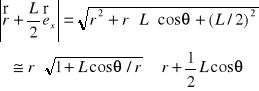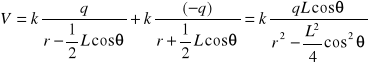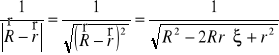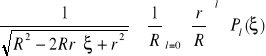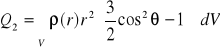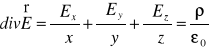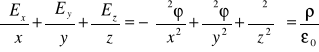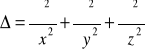Wykład 16

Różniczkowa postać prawa Gaussa. Dywergencja pola

Związek między natężeniem pola elektrostatycznego i gęstością ładunku w pewnym punkcie przestrzeni określa różniczkowa postać prawa Gaussa.

Dla tego, żeby wyprowadzić wzór na różniczkową postać prawa Gaussa rozważmy skończony obszar dowolnego kształtu o objętości . Podzielimy ten obszar na dwie części i ( ). Oznaczmy przez i powierzchnie ograniczające odpowiednio obszary i . Strumienie pola elektrycznego przez powierzchni i są równe

gdzie
.

Powierzchnie
i
zawierają tą samą powierzchnie przekroju
. A zatem, biorąc pod uwagę iż na powierzchni przekroju
dla strumieni pola elektrycznego przez powierzchnie
otrzymujemy

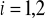
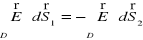
. (XVI.1)

Uwzględniając (XVI.1), całkowity strumień pola elektrycznego przez powierzchnie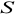
możemy zapisać w postaci

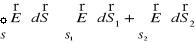
. (XVI.2)

Powtarzając podział obszaru
wielokrotnie otrzymujemy dużą liczbę małych obszarów
ograniczonych powierzchniami
. Całkowity strumień przez powierzchnie
możemy wtedy zapisać jako sumę strumieni pola elektrycznego przez poszczególne małe obszary:

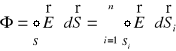
. (XVI.3)

Wprowadźmy teraz wielkość

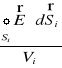
. (XVI.4)

W granicy
ze wzoru (XVI.4) otrzymujemy skalarną funkcję, która nazywa się dywergencją pola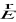

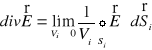
. (XVI.5)

We współrzędnych kartezjańskich dywergencja pola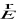
ma postać

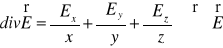
. (XVI.6)

Przez symbol nabla w równaniu (XVI.6) oznaczyliśmy operator wektorowy

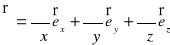
, (XVI.7)

gdzie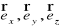
są jednostkowymi wektorami wzdłuż osi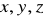
.

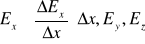
Udowodnimy wzór (XVI.6), rozważając strumień pola elektrycznego przez szczane małego sześcianu otaczającego punkt ( ). Załóżmy, że pole elektryczne w środku sześcianu czyli w punkcie ( ) ma składowe . Jeżeli sześcian jest mały, to dla składowych pola elektrycznego w punktach ( ) możemy w dobrym przybliżeniu zapisać

. (XVI.18)

W podobny sposób dla składowych pola elektrycznego w punktach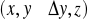
oraz (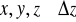
) możemy zapisać

,
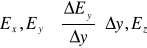
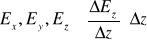
. (XVI.19)

Uwzględniając zwroty wektorów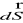
dla pola powierzchni (na zewnątrz !), dla strumienia pola elektrycznego przez szczane prostopadłe do osi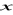
otrzymujemy

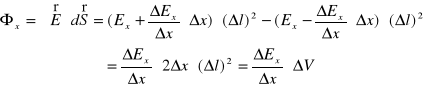
, (XVI.20)

gdzie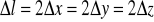
jest strona sześcianu, a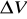
jest objętość sześcianu.

W podobny sposób dla strumienia pola elektrycznego przez szczane prostopadłe do osi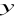
i do osi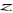
znajdujemy

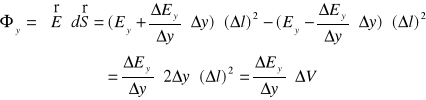
, (XVI.21)

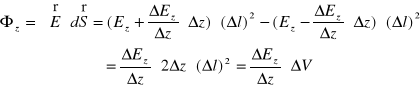
. (XVI.22)

Sumując wzory (XVI.20) - (XVI.22), dla całkowitego strumienia pola elektrycznego przez szczane małego sześcianu mamy

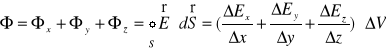
. (XVI.23)

W granicy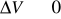
ze wzoru (XVI.23) otrzymujemy wzór (XVI.6)

.

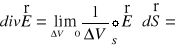
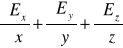
Powróćmy teraz do równania (XVI.3) i zapiszmy to równanie w postaci

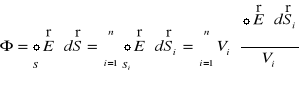
. (XVI.24)

W granice
i
nieskończenie mała objętość
przechodzi w
, wyraz w nawiasach staje się dywergencją pola
, suma zaś przechodzi a całkę objętościową

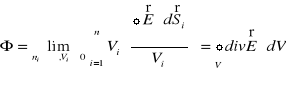
. (XVI.25)

Otrzymaliśmy więc wzór

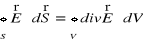
, (XVI.26)

który nosi nazwę twierdzenia Gaussa-Ostrogradskiego. To twierdzenia jest słuszne dla dowolnego pola wektorowego, dla którego istnieje dywergencja.

Zgodnie z prawem Gaussa lewa część równania (XVI.26) jest równa

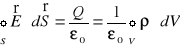
, (XVI.27)

gdzie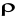
jest gęstość objętościowa ładunku.

Po podstawieniu (XVI.27) do wzoru (XVI.26) otrzymujemy

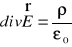
. (XVI.28)

Równanie (XVI.28) jest różniczkową postacią prawa Gaussa i wyraża lokalny związek między polem elektrycznym i gęstością ładunku w punkcie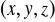
. Dla punktów nie zawierających ładunków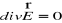
.

Potencjał pola elektrostatycznego. Krążenie

Udowodnimy, że siła Coulomba jest siłą zachowawczą oraz potencjalną. Praca którą wykonuje siła Coulomba przy przemieszczeniu ładunku
z punktu
do punktu
w polu sił ładunku
jest równa

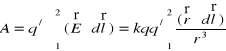
. (XVI.29)

Oznaczając 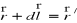, otrzymujemy . Skąd .

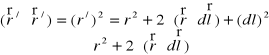
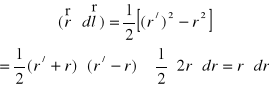
Po podstawieniu ostatniego wzoru do wzoru (XVI.29) znajdujemy

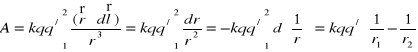
, (XVI.30)

gdzie
i
- odległości punktów
i
od ładunku
.

Ze wzoru (XVI.30) wynika, że praca wykonana przy przemieszczeniu ładunku
w polu elektrycznym ładunku
nie zależy od kształtu toru, wzdłuż którego następuje przemieszczenie; zależy ona jedynie od początkowego i końcowego położenia ładunku
względem ładunku
. Innymi słowy, udowodniliśmy, że siła Coulomba jest siła zachowawczą, a zatem jeżeli tor wzdłuż którego zachodzi przemieszczenie ładunku jest torem zamkniętym, to:

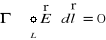
. (XVI.31)

Całka okrężna we wzorze (XVI.32) nazywa się krążeniem lub cyrkulacją natężenia pola elektrycznego. A zatem dla pola elektrostatycznego krążenie jest równa zeru. Pole wektorowe dla którego cyrkulacja jest równa zeru nazywa się polem potencjalnym. Dla takiego pola zawsze możemy wprowadzić funkcję skalarną, która nazywa się potencjalną funkcją albo potencjałem.

Ze wzoru (XVI.30) widać, że funkcja potencjalna pola elektrostatycznego wytwarzanego ładunkiem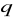
jest równa

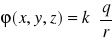
. (XVI.32)

Należy pamiętać, że podstawowym pojęciem jest różnica potencjałów, a nie sam potencjał. Istotnie, łatwo sprawdzić, że funkcja potencjalna

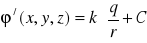
. (XVI.33)

gdzie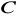
jest dowolna stała, również spełnia równanie (XVI.30)

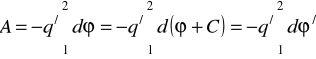
. (XVI.34)

A zatem pisząc potencjalną funkcję pola elektrycznego ładunku punktowego w postaci (XVI.32) zakładamy, że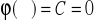
. Oczywiście, że stałą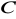
w (XVI.33) możemy wybrać w sposób dowolny. W praktyce często za powierzchnie z zerowym potencjałem wybieramy powierzchnie Ziemi.

W układzie jednostek SI za jednostkę różnicy potencjałów przyjmuje się wolt (V). Różnica potencjałów między dwoma punktami jest równa 1 woltowi , jeżeli do przemieszczenia między nimi 1 kulomba elektryczności niezbędne jest wykonanie pracy równej 1 dżulowi

.

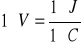
Zbiór punktów, w których potencjał elektryczny jest taki sam nazywamy powierzchnią ekwipotencjalną. Z równania (XVI.32) wynika, że ekwipotencjalne powierzchnie ładunku elektrycznego są kulami, w środku których znajduje się ładunek.

Potencjalna funkcja pola całkowicie określa pole wektorowe. Związek między składowymi natężenia pola elektrycznego i potencjałem znajdziemy korzystając ze wzorów (XVI.29) i (XVI.33)

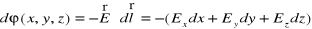
. (XVI.35)

Zmiana potencjału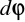
(różniczka zupełna) przy przejściu z jednego punktu do drugiego jest równa

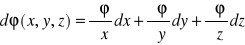
. (XVI.36)

Z porównania wzorów (XVI.35) i (XVI.36) otrzymujemy

,
,
. (XVI.37)

Mnożąc koleinie równania (XVI.37) przez wektory jednostkowe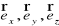
o kierunkach osi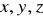
i dodając następnie je stronami otrzymujemy

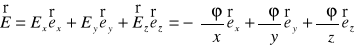
. (XVI.38)

Wyrażenie w nawiasie nazywa się gradientem funkcji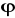
i oznacza się symbolem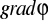
. Przez operator wektorowy nabla (XVI.7) równanie (XVI.38) możemy zapisać w postaci

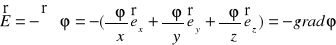
. (XVI.39)

Potencjał dowolnego rozkładu ładunków. Dipol elektryczny.

Korzystając z zasady superpozycji pól elektrycznych, potencjał dowolnego punktowego rozkładu ładunków możemy zapisać w postaci

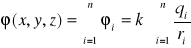
, (XVI.40)

gdzie
jest odległością punktu o współrzędnych (
) od ładunku
.

W przypadku ciągłego rozkładu ładunku potencjał pola elektrycznego w dowolnym punkcie określonym wektorem wodzącym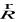
liczymy korzystając ze wzoru

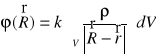
, (XVI.41)

gdzie
- wektor określający położenie elementu objętości
obszaru naładowanego od początku układu współrzędnych;
- gęstość objętościowa ładunku elektrycznego.

Jako przykład zastosowania wzoru (XVI.40) znajdziemy potencjał dipolu elektrycznego. Dipol elektryczny składa się z dwóch ładunków o przeciwnych znaków oddalonych od siebie o
. Jeżeli
to punkt P jest odległy od ładunku
o:

.

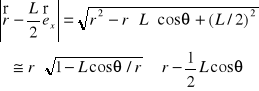
W podobny sposób odległość punktu 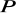od ładunku 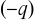wynosi Po podstawieniu tych równań do wzoru (XVI.40) dla całkowitego potencjału otrzymujemy

.

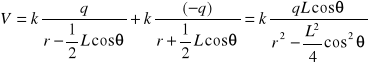
Dla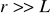
otrzymujemy ostatecznie

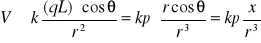
. (XVI.42)

Tu przez
oznaczyliśmy
. Wektor
nazywa się momentem dipolowym.

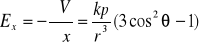
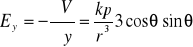
Korzystając z równania (XVI.42) i wzorów (XVI.37) dla składowych natężenia pola elektrycznego otrzymujemy , . Linii pola dipolu elektrycznego są przedstawione na rysunku.

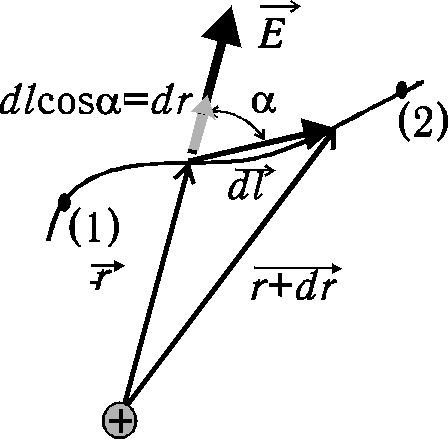
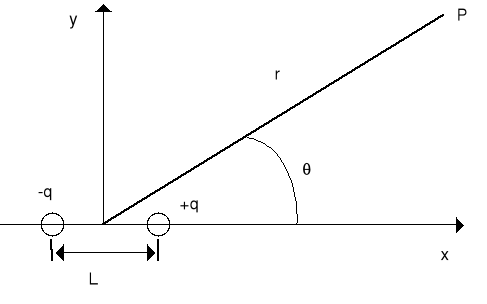
Jako przykład zastosowania równania (XVI.41) rozważmy potencjał pola elektrycznego dowolnego ciągłego rozkładu ładunków w punkcie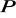
położonym w odległości dużej od naładowanego ciała. W celu wyliczenia całki we wzorze (XVI.41) wprowadźmy oznaczenie

.

Wtedy możemy zapisać

.

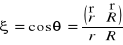
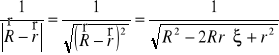
W matematyce udowodniono, że (XVI.43) gdzie 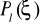są wielomianami zwanymi w matematyce wielomianami Legendre'a

,
,
itd (XVI.44)

Po podstawieniu (XVI.44) do wzoru (XVI.41) znajdujemy

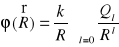
, (XVI.45)

gdzie

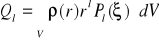
. (XVI.46)

Korzystając ze wzorów (XVI.44) otrzymujemy, że

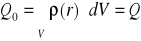
(XVI.47)

jest całkowitym ładunkiem obszaru naładowanego,

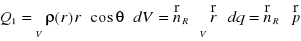
(XVI.48)

jest rzutem momentu dipolowego
układu na kierunek wektora
(
) .

Wielkość

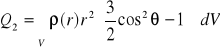
(XVI.49)

nazywa się momentem kwadrupolowym układu.

Z równania (XVI.45) wynika, że potencjał pola elektrycznego ciała naładowanego możemy rozważać jako sumę potencjału
wypadkowego ładunku układu, umieszczonego w początku układu; potencjału
wypadkowego dipola elektrycznego, umieszczonego też w początku współrzędnych; potencjału
kwadrupola itd.:

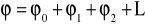
, (XVI.50)

gdzie

,
,
itd.

Równanie Poissona

Wyżej udowodniliśmy, że pole elektrostatyczne jest polem potencjalnym. Korzystając ze wzorów (XVI.37) oraz różniczkowej postaci prawa Gaussa

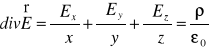
, (XVI.51)

łatwo otrzymać równanie wyrażające lokalny związek między potencjałem pola i gęstością ładunku

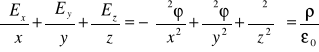
. (XVI.52)

Wprowadzając różniczkowy operator Laplace'a delta

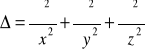
, (XVI.53)

otrzymujemy tak zwane równanie Poissona

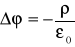
. (XVI.54)

Dla punktów gdy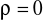
czyli dla obszarów gdy nie występują ładunki elektryczne ze wzoru (XVI.54) wynika równanie

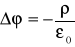
. (XVI.55)

które nazywa się równaniem Laplace'a.

17

---