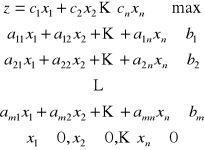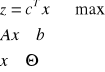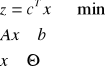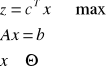BADANIA OPERACYJNE

1. Programowanie liniowe.

2. Zagadnienia transportowe.

3. Zarządzanie projektami (modele sieciowe).

1. Programowanie liniowe.

Zadanie I - Programowanie produkcji.

Przedsiębiorstwo produkuje dwa wyroby W1 i W2. Należy zaplanować produkcję przedsiębiorstwa w pewnym tygodniu w taki sposób, aby osiągnięty zysk był maksymalny, jeśli wiadomo, że produkcja wyrobów W1 i W2 jest limitowana ograniczonymi zasobami 3 środków produkcji: S1, S2, S3. Zasoby tych środków wynoszą odpowiednio: 18, 20, 24 jednostki. Nakład środka S1 potrzebny do wyprodukowania jednostki wyrobu W1 wynosi 3 jednostki, a na wytworzenie jednostki produktu W2 wynosi jednostkę. Nakłady środka S2 wynoszą odpowiednio: 1 i 2 jednostki, natomiast środka S3: 3 i 2 jednostki.

Zysk uzyskany z produkcji jednostki wyrobu W1wynosi 2 jednostki pieniężne, a z wytworzenia jednostki wyrobu W2 wynosi 3 jednostki pieniężne.

Budujemy model matematyczny zadania.

Środki produkcji	Nakłady jednostkowe		Zasoby środków produkcji
		W1		W2
S1	3	1	18
S2	1	2	20
S3	3	2	24
Zyski jednostkowe	2	3

Zmienne decyzyjne:

x₁, x₂

x₁ - wielkość produkcji W1

x₂ - wielkość produkcji W2

Funkcja celu:

f(x₁, x₂) = 2x₁ + 3x_{2 →} max

Ograniczenia:

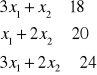
Warunki brzegowe:

Rozwiązanie zadania metodą graficzną:

Rysujemy prostą odpowiadającą pierwszemu ograniczeniu.

1.

P1 (6; 0)

P2 (0; 18)

Sprawdzamy czy otrzymana półpłaszczyzna znajduję się pod czy nad prostą. W tym celu bierzemy np. punkt o współrzędnych (0; 0) podstawiamy do nierówności i sprawdzamy, czy otrzymany wynik jest prawdziwy:

3 * 0 + 0 * 18 → prawda.

Rysujemy prostą odpowiadającą drugiemu ograniczeniu.

2.

P1 (20; 0)

P2 (0; 10)

Sprawdzamy: 0 + 2 * 0 * 20 → prawda.

Rysujemy prostą odpowiadającą trzeciemu ograniczeniu.

3.

P1 (8; 0)

P2 (0; 12)

Sprawdzamy:

3 * 0 + 2 * 0 * 24 → prawda

Wyznaczamy cześć wspólną nierówności 1, 2, 3 w pierwszej ćwiartce, (ponieważ x₁ i x₂ są nieujemne).

Zbiór decyzji (x₁ i x₂) wyznacza zbiór rozwiązań dopuszczalnych.

Rysujemy wektor wzrostu funkcji celu
Składowymi tego wektora są współczynniki funkcji celu.

Zaznaczamy warstwicę funkcji celu tj. prostą odpowiadającą wartości funkcji celu równą określonej liczbie (prosta prostopadła do wektora funkcji celu).

Warstwicę przesuwamy w kierunku wzrostu wektora funkcji celu aż do momentu zetknięcia się tej warstwicy z „ostatnim” wierzchołkiem zbioru rozwiązań dopuszczalnych.

Rozwiązaniem optymalnym naszego zadania jest punkt C o współrzędnych stanowiących punkt przecięcia prostej 2 i prostej 3.

*
*

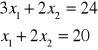
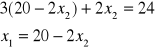
Decyzja optymalna:

Należy produkować dwie jednostki wyrobu W1 i dziewięć jednostek wyrobu W2.

To jest sytuacja, gdy zadanie posiada dokładnie jedno rozwiązanie optymalne. Jeśli zdarzy się, że warstwica zetknie się jednocześnie z dwoma wierzchołkami zbioru rozwiązań dopuszczalnych, wtedy mamy do czynienia z alternatywnymi rozwiązaniami optymalnymi.

Zadanie II mieszanek.

Należy sporządzić mieszankę składającą się z dwóch produktów P1 i P2. mieszanka ta ma dostarczyć pewnych składników odżywczych S1, S2, S3 w ilościach nie mniejszych niż określone minima.

Zawartość składników odżywczych w jednostce poszczególnych produktów podaje tablica:

Składniki odżywcze	Produkty		Minimalna ilość składników
		P1		P2
S1	1	3	9
S2	2	1	8
S3	4	1	12
Ceny jednostkowe	1	3

Należy zaplanować zakup produktu P1 i P2, aby przy minimalnych kosztach zapewnić, żeby minimalna zawartość składników była nie mniejsza niż określone minima.

METODA SIMPLEKS

Postać klasyczna zadania programowania liniowego - ograniczenia są nierównościami.

Wersja I

(a)

To samo w zapisie macierzowym:

Θ - teta (wszystkie x większe od zera)

lub

Wersja 2

(b)

Oznaczenia:

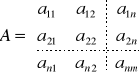
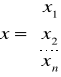
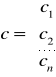
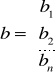
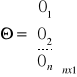
Założenie:

Postać kanoniczna zadania programowania liniowego - ograniczenia są równaniami.

(c)

Każde zadanie programowania liniowego można sprowadzić do postaci kanonicznej poprzez wprowadzenie zmiennych bilansujących v₁,v₂,…

Przykład:

- dodajemy v₁ (do lewej strony nierówności)

- odejmujemy v₂ (od lewej strony nierówności)

Wprowadzamy zmienne bilansujące:

x1	-	4x2	+	v1			=	15
2x1	-	3x2			+	v2	=	10

Postać bazowa: gdy macierz A zawiera podmacierz jednostkową.

Zmienne bazowe: zmienne odpowiadające kolumnom jednostkowym w macierzy A.

Zmienne niebazowe: pozostałe zmienne.

Rozwiązanie bazowe: rozwiązanie układu równań Ax=b przy zmiennych niegazowych równych zero.

Przykład:

2x1	+	2x2	*	14
x1	+	2x2	*	8
4x1			*	16

Przejście do postaci kanonicznej:

z

=

2x1

+

3x2

→

max

2x1

+

2x2

+

v1

=

14

x1

+

2x1

+

v2

=

8

4x1

+

v3

=

16

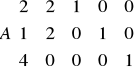
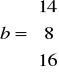
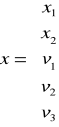
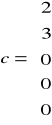
W macierzy A istnieje podmacierz jednostkowa. Zadanie jest w postaci bazowej.

zmienne bazowe: v_1, v_2, v₃

zmienne niegazowe: x_1, x₂

rozwiązanie bazowe: x₁=0, x₂=0, v₁=14, v₂=8, v₃=16,

wartość funkcji celu: z=2*0 + 3*0 = 0

Interpretacja zmiennych bilansujących v_1, v_2, v₃:

Określają jaka ilość danego środka zostanie niewykorzystana w przypadku wyboru decyzji (x_1, x₂).

Zadanie, które jest w postaci bazowej można wpisać do tablicy simpleksowej.

Oznaczenia:

baza - zmienne bazowe w danym rozwiązaniu bazowym zapisane w odpowiedniej kolejności,

c_B - ta część funkcji celu, która odpowiada zmiennym bazowym,

a_j - j-ta kolumna macierzy A,

z_j - iloczyn skalarny wektorów c_B i a_j czyli z_j = c_B * a_j.

Interpretacja z_j - jest to spadek wartości funkcji celu związany z wprowadzeniem do rozwiązania zmiennej x_j na poziomie 1.

c_j - z_j - wskaźniki optymalności (określają zmiany netto wartości funkcji celu, jeśli jednostka zmiennej x_j będzie wprowadzona do rozwiązania).

TABLICA SIMPLEKSOWA (pusta)

c^Tx→max

x1

x2

v1

v2

v3

bi

BAZA

cB

zj

cj - zj

zj

cj - zj

zj

cj - zj

…….

zadanie - cd.

c^Tx→max		x1	x2	v1	v2	v3	bi
BAZA	cB	2	3	0	0	0
v1	0	2	2	1	0	0	14	7
v2	0	1	2	0	1	0	8	4→
v3	0	4	0	0	0	1	16	---	- bez zmian (bo to jest to co chcemy)
zj		0	0	0	0	0
cj - zj		2	3*	0	0	0
v1	0	1	0	1	-1	0	6
x2	3	½	1	0	½	0	4
v3	0	4	0	0	0	1	16
zj		-1½	3	0	1½	0
cj - zj		½	0	0	-1½	0
zj
cj - zj

Liczymy wskaźniki optymalności, zj:

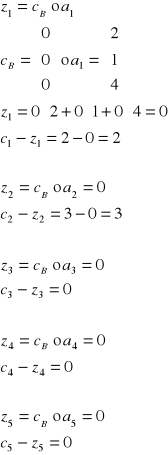
Z tablicy 1 simpleks wynika, że do bazy wchodzi zmienna x₂ (ma największy dodatni wskaźnik optymalności = 3).

Obliczamy ilorazy
,

dla pierwszego wiersza - 14:2=7,

dla drugiego - 8:2=4,

dla trzeciego - NIE WOLNO DZIELIĆ PRZEZ ZERO

a_ij - elementy kolumny zmiennej wchodzącej do bazy.

Wybieramy najmniejszy iloraz, czyli 4 - to znaczy, że zmienna v₂ opuszcza bazę.

Zaznaczamy element główny przekształcenia 2.

Przejście do sąsiedniego rozwiązania bazowego:

stosujemy operacje elementarne na wierszach macierzy układu równań odpowiadających ograniczeniom zadania.

Przykład:

Elementem głównym przekształcenia jest liczba 2 w drugim wierszu i drugiej kolumnie macierzy A (przecięcie kolumny zmiennej wchodzącej do bazy i wiersza zmiennej opuszczającej bazę).

Wybrany wiersz (z najmniejszym ilorazem) dzielimy przez element główny przekształcenia. Na pozostałe wiersze działamy wybranym wierszem pomnożonym przez odpowiednie liczby.

Nowy wiersz drugi: W₂ * ½

Nowy wiersz pierwszy: W₂ * (-1) + W₁

Nowy wiersz trzeci - bez zmian (bo a₃₂=0).

Inne wiersze obliczamy w ten sposób, że wybrany wiersz dzielimy przez element główny przekształcenia i mnożymy przez liczbę, którą zastępujemy z przeciwnym znakiem, plus dany wiersz.

Kryterium optymalności (dla maksimum).

• wartości wszystkich wskaźników optymalności są ujemne lub 0. - wtedy mamy rozwiązanie optymalne.

• Jeżeli choć jeden wskaźnik jest dodatni, to można poprawić rozwiązanie.

Wybór nowego rozwiązania bazowego (sąsiedniego - różniącego się od poprzedniego tylko jedną zmienną bazową):

1. Wybór zmiennej wprowadzanej do bazy (KRYTERIUM WEJŚCIA) - spośród wskaźników optymalności c_j - z_j wybieramy największy. Odpowiadającą mu zmienną wprowadzamy do nowej bazy.

2. Wybór zmiennej opuszczającej bazę (KRYTERIUM WYJŚCIA) - obliczamy ilorazy
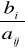
   dla a_ij>0, (i oznacza numer zmiennej wprowadzanej do bazy). W nowym rozwiązaniu bazowym rezygnujemy z tej zmiennej, dla której iloraz jest najmniejszy.

Sztuczna zmienna.

Dane jest zadanie programowania liniowego:

f(x₁,x₂)=3x₁ +2x₂ max

3x₁+2x₂≥6

-x₁+2x₂≥2

x₁,x₂ ≥0

Postać bazowa:

f=3x₁ +2x₂+0v₁+0v₂ max

I krok:

3x1	+	2x2	-	v1			=	6
-x1	+	2x2			-	v2	=	2

x₁,x_2, v₁,v₂ ≥0

Macierz ograniczeń:

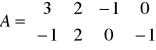
II krok:

Wprowadzamy sztuczne zmienne;

f=3x₁ +2x₂+0v₁+0v₂-Ms₁-Ms₂ max

M - duża dodatnia liczba. (Minimum 10 razy większa niż górna granica dziesiątek współczynników w równaniu - u nas 10x10, czyli 100).

3x1

+

2x2

-

v1

+

s1

=

6

-x1

+

2x2

-

v2

+

s2

=

2

x₁,x_2, v₁,v_2, s₁,s₂ ≥0

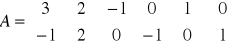
x1

x2

v1

v2

s1

s2

Tą postać wpisujemy do tablicy simpleksowej.

c^Tx→max		x1	x2	v1	v2	s1	s2	bi
BAZA	cB	3	2	0	0	-100	-100
s1	-100	3	2	-1	0	1	0	6	3
s2	-100	-1	2	0	-1	0	1	2	1→
zj		-200	-400	100	100	-100	-100
cj - zj		203	403↑	-100	-100	0	0
s1	-100	4	0	-1	1	1	-1	4	1→
x2	2	-½	1	0	-½	0	½	1	-
zj		-401	2	100	-101	-100	101
cj - zj		404↑	0	-100	101	0	-201
x1	3	1	0	-¼	¼	¼	-¼	1
x2	2	0	1	-^1/8	-^3/8	^1/8	^3/8	1½
zj		3	2	-1	0	1	0
cj - zj		0	0	1	0	-101	-100

W ostatniej tablicy należałoby wprowadzić do bazy zmienną v₁, ale dalsze postępowanie jest niemożliwe, bo wszystkie elementy wyróżnionej kolumny są ujemne.

Taka sytuacja jest sygnałem, że funkcja celu jest nieograniczona - brak rozwiązania optymalnego.

Przykład funkcji celu nieograniczonej z góry:

ZADANIE TRANSPORTOWE

Jest to problem opracowania planu przewozu pewnego jednorodnego produktu od m dostawców do n odbiorców.

Kryterium optymalizacji może w tym zadaniu uwzględniać:

1. minimalizację łącznych kosztów transportu,

2. minimalizację odległości,

3. minimalizację czasu trwania transportu.

Zadanie to rozwiązuje się algorytmem transportowym, w którym w pierwszym kroku wyznacza się pierwsze rozwiązanie dopuszczalne, które następne poprawia się w kolejnych iteracjach.

Zajmiemy się wyznaczeniem rozwiązania dopuszczalnego z zadania transportowego:

1. metodą kąta północno-zachodniego,

2. metodą minimalnego elementu macierzy kosztów.

OZNACZENIA:

Danych jest m dostawców i n odbiorców.

Liczby a₁,a₂,…,a_m - są to podaże dostawców.

Liczby b₁,b₂,…,b_n - są to zapotrzebowania odbiorców.

Na początku rozpatrujemy zadanie transportowe zamknięte (zbilansowane).

Musi być spełniony warunek:
- suma podaży = suma zapotrzebowania.

Niech x_ij oznacza wielkość produktu przewożoną od i-tego dostawcy do j-tego odbiorcy (jest to zmienna decyzyjna w tym zadaniu).

- macierz wielkości produktu.

c_ij - jednostkowy koszt przewozu produktu od i-tego dostawcy do j-tego odbiorcy.

- macierz kosztów jednostkowych.

Model matematyczny zadania wyznaczenia takiego planu przewozów, aby łączny koszt transportu był najmniejszy:

Funkcja celu -

Ograniczenia:

Typ 1. Suma
, i=1,2,…,n (Suma przewozów od i-tego dostawcy do wszystkich odbiorców równa się podaży tego dostawcy).

Typ 2. Suma
, j=1,2,…,n (Ilość produktu przewieziona do j-tego odbiorcy od wszystkich dostawców równa się zapotrzebowaniu tego odbiorcy.

Przykład:

Opracować plan przewozu cukru z dwóch hurtowni spożywczych do czterech sklepów zlokalizowanych w różnych miejscowościach. Jednostkowe koszty transportu, wielkości dostaw, zapotrzebowania sklepów podane są w tablicy:

sklepy	S1	S2	S3	S4	ai
hurtownie
H1	5	2	2	6	80
H2	1	5	8	7	80
bj	10	30	50	70	160
										160

(Elementy c_ij znajdują się wewnątrz tabeli).

Sprawdzamy czy zadanie jest zbilansowane.

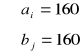
Model matematyczny:

Ograniczenia typu 1:

x₁₁+ x₁₂+ x₁₃+ x₁₄=80

x₂₁+ x₂₂+ x₂₃+ x₂₄=80

Ograniczenia typu 2:

x₁₁+ x₂₁=10

x₁₂+ x₂₂=30

x₁₃+ x₂₃=50

x₁₄+ x₂₄=70

x_ij≥0.

Algorytm transportowy

Zakładamy, że zadanie transportowe jest zbilansowane, tz.

Krok 1. Wyznaczenie pierwszego rozwiązania dopuszczalnego.

a) Metoda kąta północno-zachodniego.

Przykład:

Należy przewieść pewien produkt o 3 dostawców do 3 odbiorców.

Dane do tego zadania, a więc koszty jednostkowe, podaże dostawców, zapotrzebowania odbiorców podane są w tablicy:

odbiorcy	O1	O2	O3	ai
dostawcy
D1	17	5	6	16
D2	4	14	9	11
D3	3	9	11	23
bj	10	15	25	50

macierz kosztów

Metoda kąta północno-zachodniego polega na wypełnieniu macierzy przewozów rozpoczynając od węzła w lewym górnym rogu tablicy przewozów. Wpisujemy tam wartość minimum a₁b₁ - min(a₁b₁).

Następnie przesuwamy się w prawo lub w dół (w prawo jeśli i-temu dostawcy został produkt, w dół jeśli całą podaż i-tego dostawcy rozdzielono odbiorcom).

odbiorcy	O1	O2	O3	ai
dostawcy
D1	10*	6*		16
D2		9*	2*	11
D3			23*	23
bj	10	15	25	50

Wygenerowaliśmy w ten sposób rozwiązanie dopuszczalne, które składa się z pięciu węzłów bazowych.

W ogólnym przypadku węzłów bazowych powinno być: m+n-1, gdzie

m - liczba dostawców,

n - liczba odbiorców.

W szczególnym przypadku zdarza się, że mamy do czynienia z rozwiązaniem bazowym zdegenerowanym. Zachodzi to wtedy, gdy równocześnie w trakcie wypełniania węzłów przewozami wyzeruje się podaż i zapotrzebowanie. Wtedy należy przyjąć przewóz w węźle bazowym z wartością zero (dowolnie dla dostawcy lub odbiorcy).

b) Metoda minimalnego elementu macierzy kosztów.

Jako węzeł bazowy wybieramy węzeł, w którym macierz kosztów ma najmniejszą wartość.

W przypadku niejednoznaczności wybieramy dowolny taki węzeł. Następnie określamy wielkość przewozu dla znalezionego węzła biorąc pod uwagę minimalną wartość podaży i popytu dla wyznaczonego przez ten węzeł dostawcy i odbiorcy.

Jednocześnie określamy, czy z dalszych rozważań ma być wyeliminowany dostawca, czy odbiorca i określamy przewozy na wyznaczonej linii na poziomie zero. Postępujemy tak aż do wyczerpania wszystkich możliwości.

(Dla jasności przedstawię tok postępowania krok po kroku.)

odbiorcy	O1	O2	O3	ai
dostawcy
D1	17	5	6	16
D2	4	14	9	11
D3	3	9	11	23	najmniejsza wartość w tym węźle
bj	10	15	25	50

Wybieramy minimum (a₃,b₁): 10 i wpisujemy do węzła.

odbiorcy	O1	O2	O3	ai
dostawcy
D1				16
D2				11
D3	10			23
bj	10	15	25	50

Z dalszych rozważań eliminujemy odbiorcę O₁, ponieważ wyczerpaliśmy jego całe zapotrzebowanie.

odbiorcy	O1	O2	O3	ai
dostawcy
D1	17	5	6	16	najmniejsza wartość w tym węźle
D2	4	14	9	11
D3	3	9	11	23
bj	10	15	25	50

Wybieramy minimum (a₁,b₂): 15 i wpisujemy do węzła.

odbiorcy	O1	O2	O3	ai
dostawcy
D1		15		16
D2				11
D3	10			23
bj	10	15	25	50

Z dalszych rozważań eliminujemy odbiorcę O₂, ponieważ wyczerpaliśmy jego całe zapotrzebowanie.

odbiorcy	O1	O2	O3	ai
dostawcy
D1	17	5	6	16	najmniejsza wartość w tym węźle
D2	4	14	9	11
D3	3	9	11	23
bj	10	15	25	50

Wybieramy minimum (a₁,b₃): 1 i wpisujemy do węzła.

odbiorcy	O1	O2	O3	ai
dostawcy
D1		15	1	16
D2				11
D3	10			23
bj	10	15	25	50

Dalej już pikuś, bo zostały nam 2 węzły do wypełnienia, a więc:

odbiorcy	O1	O2	O3	ai
dostawcy
D1		15*	1*	16
D2			11*	11
D3	10*		13*	23
bj	10	15	25	50

Krok 2.

odbiorcy	O1	O2	O3	ai
dostawcy
D1		15*	1*	16
D2			11*	11
D3	10*		13*	23
bj	10	15	25	50

Macierz kosztów wraz z zaznaczonymi węzłami bazowymi:

	17	5*	6*
C =	4	14	9*
	3*	9	11*

Wyznaczamy takie liczby
oraz
, że spełniony jest układ równań:

- dla węzłów bazowych.

Zakładamy, że
=0

Robimy to obserwując macierz kosztów.

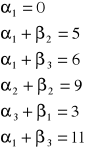
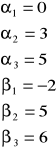
	17	5*	6*	0
C =	4	14	9*	3
	3*	9	11*	5
	-2	5	6

Następnie wyznaczamy macierz wskaźników optymalności, w której każdy wskaźnik optymalności wynosi:

Dane rozwiązanie jest optymalne jeśli wszystkie wskaźniki optymalności
są
0.

Macierz wskaźników optymalności:

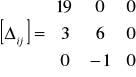
Wniosek: nasze rozwiązanie nie jest optymalne, bo istnieje ujemny wskaźnik optymalności w węźle _<3,2>.

Krok 3. Poprawa rozwiązania.

Jeśli rozwiązanie nie jest optymalne, to szukamy węzła niebazowego <k,l>, dla którego zachodzi
, NB - węzły niebazowe.

To znaczy, że szukamy wskaźnika optymalności najmniejszego wśród ujemnych. Odpowiadający mu węzeł oznaczamy <k,l>.

Generujemy nowe rozwiązanie przyjmując węzeł <k,l> jako węzeł centralny.

Następnie tworzymy cykl składający się z węzła centralnego <k,l> i węzłów bazowych.

Cykl tzn. droga zamknięta, która:

1. składa się z parzystej liczby węzłów,

2. posiada dokładnie 2 węzły w każdym wierszu i w każdej kolumnie, przez które przechodzi.

Węzły tworzące ten cykl oznaczamy na przemian plusami i minusami rozpoczynając od plusa (+) w węźle centralnym. Spośród węzłów oznaczonych minusem, wybieramy węzeł o minimalnym przewozie.

Tworzymy nowe rozwiązanie bazowe dodając ten minimalny przewóz do węzłów oznaczonych plusem (+) i odejmując go od węzłów oznaczonych minusem (-).

W naszym przykładzie węzłem centralnym będzie węzeł _<3,2>.

odbiorcy	O1	O2	O3	ai
dostawcy
D1		15*-	1*+	16
D2			11*	11
D3	10*	+	13*-	23
bj	10	15	25	50

Spośród wierzchołków cyklu wybieramy najmniejszy przewóz odpowiadający węzłom oznaczonym minusem tzn. min(13,15)=13.

Generujemy nowe rozwiązanie bazowe.

odbiorcy	O1	O2	O3	ai
dostawcy
D1		2*	14*	16
D2			11*	11
D3	10*	13*		23
bj	10	15	25	50

Sprawdzamy, czy to rozwiązanie jest optymalne. Liczymy wskaźniki optymalności.

Macierz kosztów:

	17	5*	6*
C =	4	14	9*
	3*	9*	11

Zakładamy, że
=0.

Rozwiązujemy układ równań:

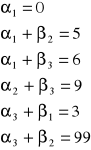
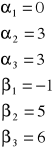
	17	5*	6*	0
C =	4	14	9*	3
	3*	9*	11	4
	-1	5	6

Macierz wskaźników optymalności:

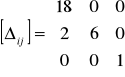
Wszystkie wskaźniki optymalności są
0. Uzyskane rozwiązanie bazowe jest optymalne.

(Koszt tak rozplanowanych przewozów jest najmniejszy.)

Modele sieciowe

Modele sieciowe to modele przedsięwzięć wieloczynnościowych.

O strukturze przedsięwzięcia decydują 2 czynniki:

1. zdarzenia, w modelu oznacza to osiągnięcie zaawansowania prac przy realizacji przedsięwzięcia. Zdarzenia będziemy oznaczali graficznie za pomocą kółek

2. czynności - jest to wyodrębniona część przedsięwzięcia charakteryzująca się momentem rozpoczęcia, trwania i momentem zakończenia. Obrazem graficznym czynności będą w modelu strzałki (łuki)

W modelach sieciowych optymalizacja polega na:

1. budowie modelu

1. ustaleniu listy czynności, z których składa się przedsięwzięcie

2. ustaleniu wierzchołka początkowego i końcowego przedsięwzięcia

3. ustaleniu sekwencji czynności tzn. ustaleniu dla każdej czynności jednej lub kilku czynności, które muszą być zakończone przed rozpoczęciem rozpatrywanej czynności

2. wyznaczanie ścieżki krytycznej w oparciu o nałożony na czynności parametry np. (czasy trwania czynności)

Ścieżka krytyczna jest to ciąg czynności rozpoczynającej się w zdarzeniu początkowym a kończącym się w zdarzeniu końcowym, które nie mogą ulec opóźnieniu w trakcie realizacji przedsięwzięcia.

Opóźnienie jakiejkolwiek czynności, leżącej na ścieżce krytycznej powoduje bowiem wydłużenie czasu trwania całego przedsięwzięcia

Założenia poprawnie zbudowanej sieci czynności

1) Istnieje dokładnie jedno zdarzenie początkowe i końcowe

Graficznie zdarzenie początkowe jest to zdarzenie do którego nie dochodzi żadna strzałka.

Zdarzenie końcowe jest to zdarzenie, z którego nie wychodzi żadna strzałka

Jeśli nie jest spełnione założenie 1 wprowadzamy czynność i zdarzenie pozorne (czas trwania tych czynności wynosi O)

2)..Zdarzenia w sieci muszą mieć numerację właściwą tzn. numer zdarzenia początkującego dowolny występujący w sieci strzałką jest mniejszy niż numer zdarzenia kończącego tę strzałkę

Zdarzenie początkowe oznaczamy nr 1 następnie usuwamy wszystkie wychodzące z niego czynności. Kolejne zdarzenia początkowe oznaczamy kolejnymi liczbami naturalnymi i tak do końca.

3). Dwa dowolnie wybrane zdarzenia może w sieci łączyć co najwyżej jedna czynność.

4) Jednej czynności odpowiada w sieci dokładnie 1 strzałka

Wyznaczanie ścieżki krytycznej (CPM)

Wyznaczamy najwcześniejsze momenty rozpoczęcia i zakończenia każdej czynności. Liczby te zaznaczać będziemy na rysunku nad strzałkami w kwadratowym nawiasie.(kolor niebieski)

Wybieramy zawsze liczbę największą np. 8 = max [3,8]

Czas trwania przedsięwzięcia T w naszym zadaniu będzie to max. z czasów zakończenia wszystkich czynności wchodzących do zdarzenia końcowego o nr5

T = max ( 6, 15, 5)

T = 15

Z wyznaczania najpóźniejszych momentów rozpoczęcia i zakończenia każdej czynności. Będziemy zapisywać te liczby w kwadratowych nawiasach pod strzałkami (kolor czerwony).

Rozpoczynamy postępowanie od zdarzenia końcowego

7 = min. (11,7)

od 7 odejmujemy czas trwania czynności

czyli 2 dni otrzymując w ten sposób parę liczb [5,7]

Ścieżka krytyczna - będą to czynności w których najwcześniejsze momenty rozpoczęcia i zakończenia każdej czynności pokrywają się z najpóźniejszymi momentami rozpoczęcia i zakończenia każdej czynności. W naszym przykładzie ścieżka krytyczna to:

Można również wyznaczyć rezerwy czasowe dla czynności niekrytycznych

czynności	rezerwy
1 - 2 2 - 5 2 - 4 3 - 5	5 - 0 = 7 - 2 = 5 11 - 2 = 15 - 6 = 9 7 - 2 = 8 - 3 = 5 13 - 3 = 15 - 5 = 10

EKONOMETRIA

Ekonometria jest nauką o metodach badania ilościowych zależności występujących między zjawiskami ekonomicznymi. Podstawowym narzędziem analizy ekonometrycznej jest model ekonometryczny.

Model ekonometryczny jest to konstrukcja formalna, która za pomocą jednego równania lub układu równań przedstawia zasadnicze powiązanie występujące pomiędzy rozpatrywanymi zjawiskami ekonometrycznymi.

Model przedstawiający zależność zmiennej objaśnianej Y od zmiennych objaśniających X₁, X₂, ........X_k zapisujemy w postaci :

Model 1) Y = f (X₁, X₂, .............Y_k ) + ξ (tj.ypsylon)

gdzie:

f - jest to określona postać analityczna zmiennych objaśniających

ξ - jest to składnik losowy

Składnik losowy przedstawia łączny efekt oddziaływania na zmienną Y tych wszystkich czynników, które nie zostały uwzględnione jako zmienne objaśniające w modelu 1)

W modelu 1) składnik losowy jest równy odchyleniom rzeczywistych wartości zmiennych Y od jej wartości teoretycznych określonych przez model. Składnik losowy jest zmienną losową.

Jednym z zadań analizy ekonometrycznej jest poznanie podstawowych charakterystyk rozkładu tej zmiennej a w szczególności jej wariancji.

W modelach ekonometrycznych występują 2 rodzaje parametrów:

1. parametry strukturalne od których zależy wartość funkcji f zmiennych objaśniających

2. parametry stochastycznej struktury modelu, czyli parametry rozkładu składnika losowego

Etapy budowy modelu ekonometrycznego.

1) Specyfikacja modelu - określamy jakie zjawisko badamy (zmienne Y), określamy jakie czynniki mają wpływ na zmienną Y (określamy X₁, X_2....., X_k)

2) Zebranie danych statystycznych

3) Estrymacja parametrów modelu

model 2) Y = ά₀ + ά₁ X₁ +......... ά _k Y_k + ξ

W przypadku modelu liniowego (zależności liniowej zmiennej objaśnianej od zmiennych objaśniających) na podstawie danych statystycznych będziemy określać liczbowe wartości ά _0, ά_{1, ...........} ά_k w modelu 2)

4) Weryfikacja modelu 5) Praktyczne wykorzystanie modelu

ETAPY BUDOWY MODELU

1. specyfikacja modelu

2. zebranie danych statystycznych

Model wielorakiej regresji liniowej:

α₀ + α₁x₁ + α₂x₂ + … + α_kx_k + ξ

lub w postaci macierzowej:

y= αx + ξ

Wektor obserwacji zmiennej objaśnianej y:

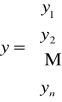
Wektor parametrów strukturalnych α:

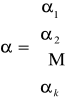
Macierz obserwacji zmiennych objaśniających:

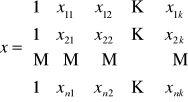
Do szacowania parametrów strukturalnych modelu można wykorzystać metodę najmniejszych kwadratów (MNK), gdy spełnione są następujące warunki:

1. Model jest liniowy względem parametrów (lub można go do takiej postaci doprowadzić poprzez transformację zmiennych).

2. Zmienne objaśniające przyjmują ustalone wartości (tzn. nie są zmiennymi losowymi).

3. Zmienne objaśniające nie są liniowo zależne między sobą.

Ocenę a parametru α znajdujemy minimalizując funkcję:

f(a)=(y-x_a)^T(y-x_a)=u^Tu=∑(u_i)²

∑(u_i)² - suma kwadratów reszt; u - reszta.

Ocena a parametru α:

Założenia klasycznej metody najmniejszych kwadratów:

1. zmienne x₁, x₂, …, x_k,

2. nie występują związki liniowe między nimi,

3. składnik losowy ξ_t ma wartość oczekiwaną równą zero oraz stałą (niezależną od bieżącego wskaźnika t) wariancję σ² wartości skończonej,

4. obserwacje pobierane do próby są niezależne, tzn. ciąg {ξ_t} jest ciągiem niezależnych zmiennych losowych,

5. składnik losowy {ξ_t}ma rozkład niezależny od zmiennych objaśniających.

TWIERDZENIE 1

Jeżeli są spełnione założenia 1-5, to wyznaczone wzorem
estymatory parametrów strukturalnych modelu są nieobciążone, czyli E(a)=α.

TWIERDZENIE 2

Jeżeli są spełnione założenia 1-5, to macierz wariancji i kowariancji estymatorów parametrów α_i dana jest wzorem:
, gdzie
jest wariancją składnika losowego ξ_t.

TWIERDZENIE 3

Jeżeli spełnione są założenia 1-5, to nieobciążoną oceną wariancji składnika losowego jest wyrażenie:

- wariancja resztowa

n - ilość obserwacji,

k - liczba zmiennych objaśniających.

Przykład:

Należy oszacować model liniowy:

y=α₀ + α₁x₁ + α₂x₂ + ξ,

mając do dyspozycji dane statystyczne podane w tablicy.

nr obserwacji	yt	x1t	x2t
1	1	2	-1
2	-1	2	2
3	0	1	-1
4	-2	-3	1
5	1	-2	-1

Dane w zapisie macierzowym:

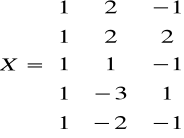
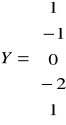
Obliczenia

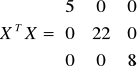
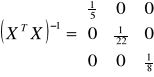
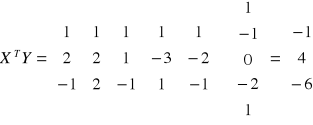
Parametry strukturalne:

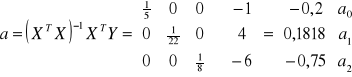
Zapis oszacowanego modelu:

y = - 0,2 + 0,1818x₁ - 0,75x₂ + u_t

interpretacja:

dla a₁ - Jeżeli x₁ wzrośnie o 1 jednostkę, to y wzrośnie o 0,1818 jednostki (przy stałych wartościach pozostałych zmiennych),

dla a₂ - Jeżeli x₂ wzrośnie o 1 jednostkę, to y zmaleje o 0,75 jednostki (przy stałych wartościach pozostałych zmiennych).

Wartości teoretyczne zmiennej y:

Reszty modelu:

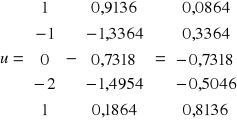
Wariancja resztowa:

- odchylenie standardowe składnika resztowego.

Macierz wariancji - kowariancji:

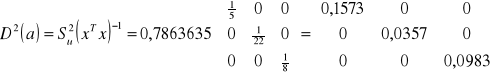
Błąd średni szacunku parametru:

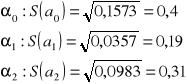
Zapis oszacowanego modelu:

y	=	-	0,2	+	0,1818x1	-	0,75x2	+	ut
			(0,4)		(0,19)		(0,31)

MACIERZ CROSS

	Y	1	x1	x2
y
1		n
x1
x2

y^Ty

y^Tx

x^Ty

x^Tx

n - suma obserwacji

Parametry strukturalne:

a=(x^Tx)^-1x^Ty

Wariancja resztowa:

[y^Ty-a^Tx^Ty]

Macierz wariancji i kowariancji:

(x^Tx)^-1

Błędy średnie szacunku:

- 31 -

2 dni

3 dni

2 dni

O dni

0 dni

3 dni

2

6

9

7

5

4

1

8

3

2 dni

3 dni

2 dni

3 dni

0 dni

Czas trwania czynności w dniach

Przesuwamy się w prawo dodając czas trwania czynności

4

2

[2,6]

1

[11,15]

[2,3]

[0,2]

[7,8]

[5,7]

2

[8,15]

7

4

5

1

[8,15]

[3,8]

3

[0,3]

[3,8]

[3,5]

[0,3]

5

[13,5]

3

2

[2, 3]

2

[3, 8]

[8, 15]

5

3

4

2

[11, 5]

4

1

[5, 7]

[7, 8]

2

1

5

4

3

1

---