E1. Narysuj schemat blokowy ilustrujący współczesne implementacje (realizacje fizyczne) systemów cyfrowego przetwarzania sygnałów (CPS)

Konwersja analogowo-cyfrowa:

(zegar) (okres próbkowania)

„Sample and hold”

gdzie:

Koncepcyjna reprezentacja systemu konwersji analogowo cyfrowej:

konwerter właściwy (digitizer)

E2. Omów poznane klasyfikacje sygnałów. Podaj przykłady.

Sygnały:

- deterministyczne(czas ściśle określony w dowolnej chwili)

- stochastyczne (nieokreślony i można określić jedynie za pomocą parametrów statystycznych)

Podstawowe kryteria klasyfikacji sygnałów wiążą się z ich cechami czasowymi. Dotyczą zakresu, ograniczoności i ciągłości zbiorów wartości argumentu i zbiorów wartości funkcji.

Sygnały:(rysunki po kolei jak nazwy)

- ciągłe z czasem ciągłym (analogowe),

- ciągłe z czasem dyskretnym (dyskretne),

- dyskretne z czasem ciągłym (skwantowane),

- dyskretne z czasem dyskretnym (cyfrowe).

E3.Jakie są zalety i wady CPS w porównaniu z techniką analogową?

ZALETY:

-gwarantowana dokładność; zależy ona tylko od liczby bitów (liczba przyjmująca dwie wartości zero i jeden)

- perfekcyjna powtarzalność; nie ma zmian wywołanych tolerancja elementów (np. nagranie cyfrowe można kopiować wielokrotnie bez jakiegokolwiek pogorszenia jakości sygnału)

- nie występuje dryft temperatury, ani skutki starzenia

- postęp w technologii półprzewodników pozwala na uzyskanie zwiększonej niezawodności, mniejszych wymiarów, niższych kosztów, niższego poboru mocy i większej szybkości

- większa elastyczność, systemy cps można oprogramować i przeprogramowywać, by uzyskać rózne funkcje bez modyfikacji sprzętu

- lepsze charakterystyki, można realizować funkcje nieosiągalne w technice analogowej(np. liniowe charakterystyki fazowe, zespolone algorytmy filtracji)

- w pewnych przypadkach informacja może być dostępna tylko w postaci cyfrowej i jedyną możliwością jest jej przetwarzanie cyfrowe

Wady cyfrowego przetwarzania sygnałów (CPS)

• układy cyfrowe pobierają znaczną moc z zasilacza (pasywne

układy cyfrowe nie są jeszcze znane),

• układy cyfrowe nie mogą przetwarzać sygnałów o bardzo dużej

częstotliwości (jednak zakres częstotliwości ciągle rośnie),

• zastosowanie CPS w środowisku analogowym wymaga użycia

przetworników AC i CA, które mogą być skomplikowane i drogie,

• przetwarzanie AC i CA sygnałów słabych (np. antenowych) i

silnych (np. sterujących głośnikiem) jest bardzo trudne;

wymagane jest stosowanie odpowiednio przedwzmacniaczy i

układów mocy w takich przypadkach,

• przetwarzanie sygnałów określonego rodzaju (np. sygnału mowy)

wymaga układów CPS o znacznie szerszym paśmie w porównaniu

do układów analogowych.

E4.Objaśnij różnice w przetwarzaniu sygnału analogowego filtrem analogowym, a systemem z filtrem cyfrowym.

(coś tego mało?? )

cyfrowy: istnieje koherentna granica pulsacji widma

analogowy: granica pulsacji jest rozmyta (dąży do zera)

E5. Objaśnij zjawisko aliasingu na przykładzie próbkowania sinusoidy.

Dla częstotliwości próbkowania mniejszej od dwukrotnej największej częstotliwości (pulsacji) sygnału (
) nie jesteśmy w stanie na wyjściu uzyskać takiego sygnału podanego na wejście. Dzieje się tak wskutek nakładania się na siebie widma sygnału próbkowanego (aliasing). Na przykładzie sinusoidy mamy:

Transformata Fouriera

jego widmo:

później znajduje się wykres widma sygnału spróbkowanego
z częstotliwością próbkowania (pulsacja próbkowania)

a więc sygnału uzyskamy na wyjściu (zrekonstruowany):

bez aliasingu:

sygnał na wyjściu (w pełni odtworzony):

Obserwujemy więc zmianę w pulsacji (częstotliwości) sygnału zrekonstruowanego w przypadku wystąpienia zjawiska aliasingu.

E6. Napisz twierdzenie Nyquista o próbkowaniu równomiernym. Co nazywamy częstotliwością Nyquista, szybkością Nyquista i przedziałem Nyquista?

Tw. Niech
będzie sygnałem o ograniczonym widmie, tzn.:

tzn.dla

Wówczas
jest jednocześnie określone przez ciąg swoich próbek:

jeśli:

częstotliwość próbkowania

lub inaczej:

czyli jeśli częstotliwość próbkowania jest co najmniej dwukrotnie większe od maksymalnej częstotliwości w widmie sygnału
.

Minimalne częstotliwości próbkowania, przy której można jeszcze odtworzyć sygnał
bez zniekształceń, tzn częstotliwość
nazywa się szybkością Nyquista. Odpowiadający jej maksymalny okres próbkowania
nazywa się przedziałem Nyquista. Częstotliwość Nyquista to
.

E7. Narysuj schemat blokowy przetwornika C/D traktując przetwarzanie dwustopniowo> Napisz wzory na przebiegi czasowy x(t) i jego widmo X(jΩ) na wyjsciu pierwszego bloku.

C/D przetwornik czasu ciągłego na dyskretny

-czas ciagly

Przedstawiony zostal schemat blokowy reprezentujący idealny konwerter czasu ciągłego na czas dyskretny, czyli idealny układ próbkujący. W ogólności operacja probkowania nie jest odwracalna. Aby zapewnic odtwarzalność sygnal Xc(t) musi spełniać zalozenie Fp>2F_M

Reprezentacja operacji probkowania, jako procesu dwustopniowego:

- mnożenie przez ciag impulsow Diraca

- zamiana sekwencji impulsow na ciag dyskretny.

Dziedzina czasu
-dystrybucja grzebieniowa

Z właściwości próbkującej

, bo =>

Dziedzina częstotliwości - znajdujemy widmo x_p(t)

Oznaczamy x_c(jΩ)=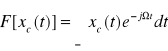
, Ω[rad/s] - pulsacja analogowa

Wniosek: Widmo sygnalu x_p(t) jest superpozycja okresowa powtarzających się widm sygnalu ciągłego x_C(t). Kolejne składniki Xp(jΩ) sa poprzesuwane o całkowita wielokrotność pulsacji próbkowania Ωp.

E8. Zilistruj przypadki konwersji C/D: bez aliasingu i z aliasingiem, poslugujac sie widmem.
Przyjmujemy, ze
dla
tzn. Najwieksza niezerowa skladowa w widmie
jest skladowa pulsacji

W wyniku konwersji C/D widmo
zostaje pomnozone przez dystrybucje grzebieniowa δ(t).

Otrzymujemy

1. bez aliasingu

2. z aliasingiem (widma składowe nie są rozłączne (nakładają się) -> zniekształcenie aliasowe)

T

E9. Objaśnij w jaki sposób można odtworzyc sygnal ciągły x_C(t) na podstawie sygnalu x_p(t) o reprezentacji w postaci delty Diraca?

Można odtworzyc x_C(t) na podstawie x_p(t) za pomocą idealnego filtru dolnoprzepustowego, takiego, ze:

Charakterystyka czestotliwosciowa filtru dolonoprzepustowego

<- filtr rekonstrukcyjny

Filtr rekonstrukcyjny

Wówczas w układzie:

Widmo sygnalu wyjściowego ma ta sama postac, jak widmo sygnalu x_C(t)

Musi być spełnione twierdzenie o probkowaniu.

E10. Do czego sluzy formula interpolacyjna Shannona i jak wyglada? Podaj przykłady interpolacji graficznej.

Formula interpolacji Shannona stosowana jest do ostworzenia x_C(t) na podstawie x [n].

Przyjmujemy, ze Ω_g=Ω_p/2=Π/T

Wtedy: H_d(jΩ)=T dla |Ω|<Π/T; 0 dla|Ω|>Π/T

Odp. Impulsowa z def. F^-1

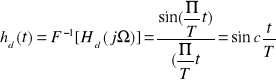
Wówczas:

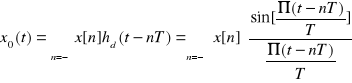
FORMULA INTERPOLACYJNA SHANNONA

Ponieważ h_d(0)=1 oraz h_d(nT)=0 dla n=+-1,+-2,.. jeżeli x[n]= x_c(nT) wówczas: X₀(nT)= X_C(nT) dla wszystkich całkowitych n, niezależnie o T (probki x₀ i x_C sa takie same) Caly przebieg x_C jest skonstruowany na bazie funkcji sinc()

gdzie
; sin(0)=1

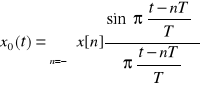
Idealny system (X₀(t)=X_C(t)) odtwarzający sygn. Ciągły.

E11. Na czym polega idea przetworniak D/C (schemat)? Co oznacza skrót?

D/C - przetwornik czasu dyskretnego na ciagly

E12. Narysuj schematy blokowe:

a) idealnego dyskretnego-czasowego systemu przetwarzania sygnałów analogowych

b) systemu cyfrowego przetwarzania sygnałów analogowych.

Ad a)

Ad b)

AAF -anti aliasin filter, SiH - sample and hold, A/D - analog to digital converter

D/A - digital to analog converter RF - reconstruction filter

E13. Zdefiniuj i narysuj charakterystykę częstotliwościową analogowego filtru antyaliasingowego (AAF).

AAF - stosuje się aby wymusić warunek, żeby częstotliwość próbkowania była co najmniej 2-krotnie większa od maksymalnej częstotliwości w widmie sygnału analogowego.

Charakterystyka :

Filtr praktyczny ma pasmo przejściowe od Ωpas i pasmo zaporowe od Ωstop, przy czym :

Ωpas <Ωstop <= Ωo/2

Ωp - pulsacja próbkowania

Ωpas - pulsacja graniczna pasma przepustowego AAF tj. najwieksza pulsacja jaka ma być wiarygodnie zachowana w sygnale sprobkowanym.

Ωstop - pulsacja graniczna pasma zaporowego

E14. Objaśnij podstawowe cechy analogowego filtru Butterwortha jako filtru AAF. Na jakiej podstawie określa się rząd tego filtru (liczbę biegunów transmitancji) ?

* Antyaliasingowy filtr dolnoprzepustowy Butterwortha jest filtrem maksymalnie płaskim, o charakterystyce amplitudowej malejącej monotonicznie w paśmie zaporowym.

* Rząd filtru można określić na podstawie charakterystyki amplitudowej podniesionej do kwadratu :

, gdzie N - rząd filtru

* Maksymalnie plaska charakterystyka amplitudowa dla Ω=0 wynika stad iż (2N-1) pochodnych z funkcji
w tymże punkcie (Ω=0) jest równych zeru.

* Wzmocnienie opisywanego filtru wyraża się wzorem :

G(Ω)= 10 log
= 20 log
, z którego łatwo odczytać ze dla :

- Ω=0 => G(0) = 0

- Ω= Ωc => G(Ωc) = 10 log(1/2)
-3dB

(dlatego właśnie pulsacje odcięcia nazywamy 3-decybelową)

* Róznica poziomów tłumienia (w [dB]) dla Ωpas i Ωo okreslona jest przez :

10 log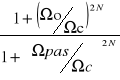


, gdzie :

Ωo = Ωp - Ωpas

Ωp - minimalna częstotliwość próbkowania

Ωpas - pulsacja graniczna pasma przepustowego

Ωc- pulsacja odciecia

E15. W jakim celu stosuje się nadprobkowanie sygnału analogowego? Na czym ono polega ? Objaśnij posługując się rysunkiem widma sygnalu.

Nadprobkowanie sygnalu analogowego stosuje się w celu zmniejszenia rzedu filtru (filtry analogowe wysokiego rzedu sa bardzo drogie). Idea polega na tym, ze o rzedzie filtru decyduje szerokość pasma przejściowego. Rzad N jest tym mniejszy im szersze pasmo przejściowe, a wiec im wieksza częstotliwość próbkowania Ωp.

Przy dwukrotnym nadprobkowaniu sygnalu, pasmo przejściowe filtru jest ponad 3-krotnie szersze. Te wymagania spelnia filtr o mniejszym rzedzie.

E16. Narysuj konfiguracje fizyczna konwersji analogowo-cyfrowej z układem „samlple & hold” i konwerterem „walsciwym” A/O. Objaśnij dzialanie układu ZOH i zilustruj odpowiednim rysunkiem.

Na wstepie układu S & H sygnal zostaje przemnożony z sygnalem „grzebieniowym” - ciagiem impulsow Dirac'a. Układ ZOH pobiera w takt wystepowania impulsow probki i podtrzymuje je na swym wyjsciu do nastepnego impulsu.

E17. Koncepcyjna reprezentacja systemu konwencji analogowo-cyfrowej z próbkowaniem i

kwantowaniem i kodowaniem binarnym.

Kod offsetowy binarny - symbole sa przypisywane w kolejności numerycznej rozpoczynając od najmniej znaczącego poziomu kwantowania.

Kod U2 - najbardziej na lewo położony bit (MSB) jest bitem znaku a pozostale bity reprezentuja liczby całkowite lub ulamki.

Liczba poziomow kwantowania :

Krok kwantowania :

B - liczba bitow w „B+1 bitowym” slowie, rozdzielczość konwertera.

E18. Kwantyzator

system nieliniowy transformujący próbkę wejsciowa x[n] w próbkę x^[n] nalezaca do skończonego zbioru scisle określonych wartości. Operacje otrzymywania skwantyzowanej probki zapisujemy : x^[n]=Q(x[n]). Operacja kwantyzacji nie jest odwracalna.

E19. Założenia statystycznego modelu błędu kwantowania.

x[n] x[n]=x[n]+e[n]

e[n]

Założenia statystycznego modelu błędu kwantowania:

1. Ciąg błędów e[n] jest dyskretnym, stacjonarnym procesem stochastycznym.

2. Ciąg błędów jest nieskorelowany z ciągiem x[n].

3. Zmienne losowe procesu błędu są nieskorelowane tzn. ciąg błędu jest białym szumem.

4. Rozkład prawdopodobieństwa procesu błędu jest równomierny w zakresie błędu kwantowania.

P[e]

1/Δ

-Δ/2 Δ/2

Czyli: e[n] to biały szum o równomiernym rozkładzie prawdopodobieństwa, wartość średnia to 0, wariancja (moc szumu):

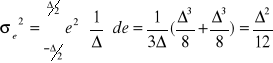
E20. Zdefiniuj współczynnik SNR.

SNR - Signal to Noise Ratio - stosunek mocy sygnału do mocy szumu - miara degradacji sygnału przez szum addytywny.

Dla (B+1) - bitowego kwantyzatora bipolarnego:

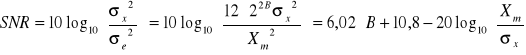
[dB]

σ_e² - moc szumu

σ_x² - moc sygnału do kwantyzacji

X_m - zakres kwantowania

σ_x - wartość średniokwadratowa amplitudy sygnału (RMS)

• dla sinusoidy:
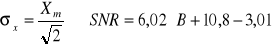
  [dB]

• dla gaussowskiego rozkładu:
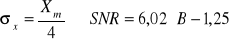
  [dB]

Model szumowy praktycznie działa dla 8 lub więcej bitów przy pełnym wysterowaniu. Obliczenia SNR są prawdziwe jedynie wtedy, gdy starannie dopasujemy zakres sygnału wejściowego do pełnego zakresu konwertera A/D

E21. W pewnym systemie CPS a) sinosoidalny sygnał o amplitudzie X_m; b) sygnał o gaussowskim rozkładzie amplitudy próbkuje się z częstotliwością Fp=20kHz i kwantuje za pomocą kwantyzatora bipolarnego w pełnym zakresie 2X_m=2V. Określ liczbę bitów kwantyzatora taką, aby średniokwadratowy błąd kwantyzacji σ_e<1μV. Oblicz przepływność bitową i zakres dynamiczny kwantyzatora.

Wariancja błędu (szumu) kwantyzacji:
, gdzie krok kwantyzacji
. Stąd średniokwadratowy błąd kwantyzacji:
. Z tego wzoru B wynosi:

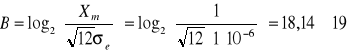
Opowiada to liczbie 2^B+1=2²⁰=1048576 - poziomów kwantyzacji.

Dla takiego B:

Przepływność bitowa wynosi zatem:

Zakres dynamiczny (SNR) kwantyzacji sterowanego sygnałem gaussowskim wynosi około:

a wysterowanego w pełni sinusoidą:

.

E22. Jaką minimalną częstotliwość próbkowania Fp należy zastosować do sygnału x(t)=cos(2*pi*Fo*t) by można go było odtworzyć jednoznacznie na podstawie ciągu próbek x[n] pobranych równomiernie co T sekund. Jaki zachodzi związek między Fp a T.

Fp > 2*Fo <= wynika z tw.Nyquista bo sygnal jest sinusoidalny czyli w widmie posiada deltę Diraca, więc wzór jest bez znaku równości

T = 1/Fp <= wiadomo

E23. Jak definiujemy sygnał?

Def. encyklopedyczna:

Przebieg fizyczny (elektryczny, radioelektryczny lub optyczny) słuzący do przenoszenia informacji między dwoma odbiornikami.

Klasyfikacja sygnałów:

1.

• deterministyczne - opisywane wprost

• stochastyczne - przypadkowe, opisywane statystycznie poprzez wielkości opisujące losowość sygnału

2.

• ciągłe z czasem ciągłym - analogowe (sygnał fizyczny zmieniający się w sposób ciągły)

• ciągłe z czasem dyskretnym - dyskretne

• dyskretne z czasem ciągłym - skwantowane

• dyskretne z czasem dyskretnym - cyfrowe (sygnał fizyczny, dwustanowy)

E24. Ogólny podział systemów przetwarzania sygnału.

Klasyfikacja systemów dyskretnych:

• systemy bezpamięci - jeśli odpowiedź y[n] dla każdego n zależy tylko od wymuszenia x[n] dla tej samej wartości n, to mówimy że system nie posiada pamięci;

• systemy przyczynowe - jeśli dla każdej liczby całkowitej n₀ próbka odpowiedzi dla n=n_o zależy tylko od próbek wymuszenia o indeksach
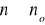
  . Krótko zapisujemy:

jeśli x₁[n]=x₂[n] dla

to y₁[n]=y₂[n] dla

Przykłady:

1. idealny system opoźniający →
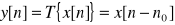
   , gdzie n₀ to liczba całkowita, nazywana opóźnieniem systemu. System bezpamięciowy tylko dla n₀=0. Liniowy, stacjonarny, stabilny, przyczynowy jeśli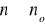
   

dla n₀=3

0 1 2 3 0 1 2 3 4 5 6

2. system wzmacniający średnią bieżącą:

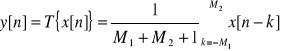
n-ta próbka ciągu wyjściowego jest obliczona jako średnia (M₁+M₂+1) próbek ciągu wejściowego otaczających próbkę n-tą. Liniowy, stacjonarny, stabilny. Przyczynowy gdy M₁≥ 0 i M₂≥ 0.

Bez pamięci tylko gdy: M₁=M₂=0

3. akumulator:

Liniowy, przyczynowy, z pamięcią. Nie jest stabilny.

E25. Jakie warunki należy spełnić by reprezentację sygnału ciągłą i dyskretną można było uważać za równoważne?

Tw. Nyquista o próbkowaniu równomiernym.

Niech x_l(t) będzie sygnałem ograniczonym o widmie tzn x_l(jΩ)=0 dla |Ω| > Ω_M [rad/s]

Wówczas x_l(t) jest jednoznacznie określone przez ciąg swoich próbek x[n]=x_l(nT) n=0,±1,..

jeżeli Ω_P= (2π)/T = 2πF_P > 2Ω_M lub inaczej (częstotliwość w MHz) F_P > 2 F_M, czyli jeśli częstotliwość próbkowania jest co najmniej 2-krotnie większa od max częstotliwości w widmie sygnału x_l(t).

Tak więc minimalna częst. próbkowania, przy której można jeszcze odtworzyć sygnał x(t) bez zniekształceń, czyli częst. F_P=2F_M nazywa się szybkością Nyquista. Odpowiadający jej max okres próbkowania T= 1/F_P = 1/2F_M zazywa się przedziałem Nyquista.

E26. Zdefiniuj podstawowe operacje wykonywane na sygnałach dyskretnych (ciągach liczowych)

-- System opóźniający y[n]=T{x[n]}=x[n-n₀] n₀- dodatkowa całkowita [opóźnienie systemu]

-- Średnia bieżąca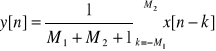
, n-ta próbka jest obliczana jako średnia (M₁+M₂+1) próbek ciągu wejściowego otaczających próbkę n-tą.

-- Akumulator

-- Różnica wprzód y[n] = y[x+1] - x[n]

-- Różnica wstecz y[n] = x[n] - x[n-1]

-- Kompensator y[n] = x[M·n] => wyselekcjonowanie M-tej próbki ciągu wejściowego

E27. Impuls jednostkowy czyli delta Kroneckera

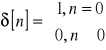
Skok jednostkowy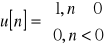

Ciąg wykładniczy rzeczywisty x[n]=aⁿu[n]

Ciąg wykładniczy zespolony x[n]=A*e^jan

Ciąg oscylacyjny - charakteryzuje się przejściami (przejściem) przez zero. np.:

Ciąg harmoniczny x[n]=Acos(ωt+φ)

Ciąg sinusoidalny x[n]=Asin(ωt).

E29. Sygnały okresowe

Sygnał okresowy x(t) z czasem ciągłym.

x(t)

Sygnał powtarza się w określonych okresach, jest zdefiniowany w każdej chwili czasowej.

Sygnał okresowy z czasem dyskretnym (dyskretny) - ciąg liczbowy {x[n]}, którego elementami są próbki x[n]sygnału ciągłego (analogowego) pobierane w chwilach t_n=nT_s, gdzie T_s jest okresem próbkowania.

x[n], n=0,±1,±2,..

Ciąg x[n] dyskretny nieokresowy: spróbkowana wartość napięcia na kondensatorze w obwodzie prądu elektrycznego.

Ciąg x[n] dyskretny cos, okresowy: spróbkowana cosinusoida z generatora.

E30. Jaki zachodzi związek pomiędzy częstotliwością (lub pulsacją) analogową a dyskretną ?

gdzie:
- pulsacja dyskretna (unormowana względem T), ω - pulsacja analogowa.

E31. Podaj operatorową definicje systemu dyskretnego

Def: System dyskretny to operator który przekształca ciągi WE x[n] w ciąg WY y[n]

y[n] = T{x[n]} {x[n]} => {y[n]}

Operator T{
} określa właściwości systemu dyskretnego, czyli sposób przekształcenia { x[n] } w { y[n] }

W ogólności n - ta próbka y[n] może być funkcja wszystkich próbek x[n]

E32. Zdefiniuj następujące systemy dyskretne: bez pamięci, liniowy, stacjonarny (niezmienny względem przesunięcia), przyczynowy, stabilny

Def. System dyskretny to operator, który przekształca ciąg wejściowy x[n] w ciąg wyjściowy y[n]:

y[n] = T { x[n] }

System bez pamięci: Jeżeli odpowiedz y[n] dla każdego n zależy tylko od wymuszenia x[n] dla tej samej wartości n, to mówimy, ze system nie posiada pamięci.

Np. - System opisany zależnością: y[n] = ( x[n] )² dla wszystkich n [NIE MA PAM.]

- y[n] = ( x[n-1] )² [Z PAMIĘCIĄ]

System liniowy: spełnia zasadę superpozycji; jeżeli { x₁[n] } => { y₁[n] } oraz

{ x₂[n] } => { y₂[n] } to system dyskretny jest liniowy W.I.T.W gdy:

T{ ax₁[n] + bx₂[n] } = aT { x₁[n]} + bT { x₂[n]}

System stacjonarny: spełnia następujący warunek:

Jeżeli x[n] => y[n] oraz x₁[n] = x[n-n₀]

n₀ - całkowite to:

y₁[n] = y[n-n₀]

System przyczynowy: System jest przyczynowy, jeżeli dla każdej liczby całkowitej n₀ próbka odpowiedzi dla n = n₀ zależy tylko od próbek wymuszenia o indeksach

n ≤ n₀. Krotko zapisujemy:

Jeżeli: x₁[n] = x₂[n] dla n ≤ n₀

To: y₁[n] = y₂[n] dla n ≤ n₀

System stabilny: System dyskretny nazywamy stabilnym W.I.T.W, gdy ograniczony ciąg wejściowy daje w odpowiedzi ciąg ograniczony, tzn.

Jeśli:
to

Gdzie
i
<

E33. Co oznacza skrót: system DSL?

DLS = DYSKRETNY, LINIOWY, STACJONARNY

DYSKRETNY SYSTEM: to operator, przekształca ciąg wejściowy x[n] w ciąg wyjściowy y[n]:

y[n] = T{x[n]} {x[n]} => {y[n]}

Operator T{
} określa właściwości systemu dyskretnego, czyli sposób przekształcenia { x[n] } w { y[n] }

LINIOWY SYSTEM: spełnia zasadę superpozycji, tzn. jeżeli spełnia zasadę superpozycji; jeżeli { x₁[n] } => { y₁[n] } oraz { x₂[n] } => { y₂[n] } to system dyskretny jest liniowy W.I.T.W gdy:

T{ ax₁[n] + bx₂[n] } = aT { x₁[n]} + bT { x₂[n]}

STACJONARNY SYSTEM: niezależny względem przesunięcia

Jeżeli x[n] => y[n] oraz x₁[n] = x[n-n₀]

n₀ - całkowite to:

y₁[n] = y[n-n₀]

(opóźnione w czasie pobudzenie => opóźniona odpowiedz)

E34. Podaj definicje idealnego systemu opóźniającego i zilustruj jego działanie na dowolne wylosowanym ciągu. Jakie są właściwości tego systemu?

Idealny system opóźniający jest to system opisany zależnością:

y[n] = T{ x[n] } = x[n-n₀]

dla -
<n<

n₀ - liczba całkowita dodatnia nazwana opóźnieniem systemu

System przesuwa ciąg wejściowy w prawo o n₀ próbek. Jeżeli n₀ jest liczbą całkowitą ujemna - przesuwamy w lewo oznacza to wyprzedzenie w czasie np. dla ciągu

dla opóźnienia n₀ = 3 mamy

Właściowści:

• System jest bez pamięci, jeśli n₀ = 0

• Liniowy

• Stacjonarny

• Przyczynowy, jeśli n₀ ≥ 0

E35. Zdefiniuj system wyznaczający średnią bieżącą. Jakie są jego właściwości? Podaj przykład zastosowania tego systemu.

System wyznaczający średnia bieżącą zdefiniowany jest równaniem:

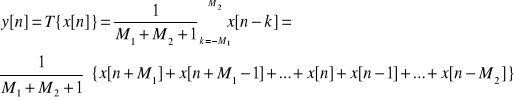
n - ta próbka ciągu wejściowego jest obliczana jako średnia (M₁+M₂+1) próbek ciągu wejściowego otaczających próbkę n - tą.

Właściwości systemu:

• liniowy, stacjonarny, stabilny

• przyczynowy gdy M₁≥0 oraz M₂≥0

• nie posiada pamięci jedynie, gdy M₁=M₂=0

E36. Zdefiniuj: akumulator, kompresor oraz system różnicy w przód I wstecz. Jakie są ich zastosowania? Podaj przykład zastosowania systemu.

AKUMULATOR

Def.

Właściwości:

- liniowy, przyczynowy, z pamięcią

• nie jest stabilny (chociaż y[n] jest skończony dla końcowego n)

• nie jest ograniczony, tzn. nie istnieje takie
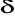
  >0, że dla każdego n |y[n]| <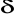
  

Przykład odpowiedzi impulsowej (systemów DLS):

nieskończona odpowiedz impulsowa

Transmitancja h[n] = u[n]

H(z) = Z{ u[n] } =

Zastosowanie jako układ całkujący

KOMPRESOR

Def.

M - całkowita liczba dodatnia

Właściwości: ciąg liczbowy wyjściowy jest przez wyselekcjonowanie każdej M-tej próbki ciągu wejściowego. System nie jest stacjonarny, widać to z przykładu.

Niech x₁[n] => y₁[n] oraz

x₁[n] => x[n - n₀]

wówczas y₁[n] = x₁[Mn] = x[Mn - n₀]

Dla systemu stacjonarnego musi zachodzić:

y[n - n₀] = x[M(n - n₀)] ≠ y₁[n]

a tu zachodzi jedynie dla n=1.

RÓŻNICA W PRZÓD I WSTECZ

Def. W przód y[n] = x[n + 1] - x[n]

system nie jest przyczynowy, bo występuje x[n+1]

Wstecz y[n] = x[n] - x[n-1]

przyczynowy

Przykład odpowiedzi impulsowej (system DLS)

różnica w przód: h[n] = δ[n + 1] - δ[n]

różnica wstecz: h[n] = δ[n] - δ[n - 1]

Transmitancje:

różnica w przód: h[n] = δ[n + 1] - δ[n] => H(z) = z - 1

różnica wstecz: h[n] = δ[n] - δ[n - 1] => H(z) = 1 - z ^-1

Zastosowanie różnicy wstecz jako różniczkowanie.

E37. Podaj definicję odpowiedzi impulsowej systemu DLS.

Dla systemu DLS definiuje się odpowiedź impulsową h[n], dla n=±1,...

Df. h[n] to odpowiedź impulsowa systemu DLS na impuls jednostkowy (δ[n] - delta Kroneckera) przy zerowych warunkach początkowych. h[n] całkowicie charakteryzuje system DLS.

Odpowiedź y[n] systemu DLS na dowolne pobudzenie x[n] jest splotem dyskretnym ciągów: pobudzenie x[n] i odpowiedzi impulsowej h[n]. Splot dyskretny jest przemienny.

E38. Podaj warunki stabilności i przyczynowości systemu DLS, wyrażone za pośrednictwem odpowiedzi impulsowej.

Układ stabilny definiujemy jako układ, w którym każde ograniczone pobudzenie powoduje ograniczoną odpowiedź. Układy liniowe, niezmienne względem przesunięcia^* są stabilne gddy:

Układ przyczynowy jest to układ, w którym zmiany na wyjściu nie poprzedzają zmian na wejściu. Oznacza to, że dla układów przyczynowych, jeśli x₁[n]=x₂[n], n<n₀, to y₁[n]=y₂[n], n<n₀.

Układ liniowy niezmienny względem przesunięcia jest przyczynowy gddy jego odp. Impulsowa dla n<0 ma wyrazy równe zeru. Z tego względu wygodnie nazywać ciąg zerowy dla n<0 ciągiem przyczynowym rozumiejąc, że mógłby on być odp. Impulsową układu przyczynowego.

Jako przykład stabilności i przyczynowości można rozpatrzyć układ liniowy niezmienny względem przesunięcia o odp. Impulsowej h[n]=aⁿu[n]. Ponieważ odp. Impulsowa jest zerowa dla n<0, układ jest przyczynowy. Aby określić stabilność musimy obliczyć sumę:

Jeśli |a|<1, suma postępu geometrycznego istnieje i jest równa
. Jednak jeśli |a|>=1, szereg jest rozbieżny, a zatem układ jest stabilny tylko dla |a|<1.

^*Układ niezmienny względem przesunięcia charakteryzuje się przez właściwość, że jeśli y[n] jest odp. na pobudzenie x[n] to y[n-k] jest odp. na x[n-k], gdzie k to dodatnia lub ujemna liczba całkowita.

E39. Jaką odpowiedź impulsową ma połączenie kaskadowe, a jaką połączenie równoległe systemów DLS? Narysuj te połączenia.

(na rysunkach na wejściu jest x[n] na wyjściu y[n] )

1. kaskadowo: odp. impulsowa takiego systemu to: h[n]=h₁[n]*h₂[n]

2. równolegle: odp. impulsowa takiego systemu to h[n]=h₁[n]+h₂[n]

E40. W jakim celu stosuje się splot odpowiedzi impulsowej z sygnałem wejściowym systemu dyskretnego? Przytocz odpowiednie wzory.

Celem splotu odp. impulsowej h[n] z sygnałem wej. x[n] jest obliczenie odpowiedzi y[n] systemu.

Odpowiedź y[n] systemu DLS na dowolne pobudzenie x[n] jest splotem dyskretnym ciągów: pobudzenie x[n] i odpowiedzi impulsowej h[n]. Splot dyskretny jest przemienny.

E41. Oblicz wynik {y[n]} splotu ciągów:
za pomocą

dowolnej metody.

Najszybciej można to zrobić metodą mnożenia, ale należy uważać na kropkę (kropkę stawiamy przed wartością współczynnika dla n=0)

{y[n]}_n=-1={3,8,14,8,3}

E42. Zdefiniuj dyskretno-czasowe przekształcenie Fouriera (DTFT) i przekształcenie do niego odwrotne. Objaśnij symbole występujące w tych wzorach.

Dyskretno-czasowe przekształcenie Fouriera (DTFT)
, odwrotne: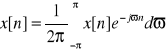
(IDTFT DTFT^-1)

- widmo sygnału

x[n] - ciąg próbek

E43. Na podstawie DTFT narysuj widma :amplitudowe i fazowe sygnału
dla wybranej wartości „a”

- transformata ciagu x[n]

Dla a = 0,5

Widmo amplitudowe:

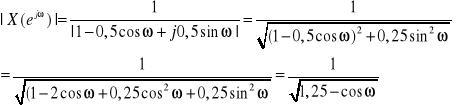
=0

=
=2

=

=
=0,66

=

=

Widmo fazowe:

=0 arg=0

=
arg=0

=
arg=-arctg(0,5)

E44. Zdefiniuj charakterystyki: amplitudowo-fazową, amplitudową i fazową systemu DLS o odpowiedzi impulsowej h[n]=a ⁿu[n]. Narysuj te charakterystyki dla wybranej wartości a takiej, która zapewnia stabilność tego systemu.

Charakterystyka amplitudowo fazowa:
dla |d|<1

Amplitudowa: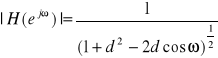
; fazowa:

E45. Własności DTFT

Jeżeli x[n] ↔ X(e ^{j ω}) i y[n] ↔ Y (e ^{j ω}) to słuszne są następujące twierdzenia:

1. O liniowości:

2. O przesunięciu w dziedzinie czasu
; n_o - całkowite

3. O przesunięciu w dziedzinie częstotliwości:

4. O różniczkowaniu względem częstotliwości:

5. O energii (Parsevala):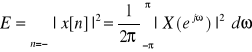

6. O splocie:

7. O iloczynie: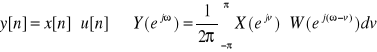

E46. Wiadomo, że DTFT ciągu x[n] wynosi X(e^jω). Jakie są transformaty ciągów:

1. x₁[n]=x[n-5], b) x₂[n]=x[n]e^j5n, c) x₃[n]=aⁿx[n], d) x₄[n]=nx[n]

1. x₁[n]=x[n-5], z twierdzenia o przesunięciu w dziedzinie czasu

x[n-n₀] ⇔ e^-jωn0 X(e^jω) , n₀ - całkowite

x[n-5] ⇔ e^-jω5 X(e^jω) , n₀ - całkowite

2. x₂[n]= x[n]e^j5n, z twierdzenia o przesunięciu w dziedzinie częstotliwości

x[n] e^jωn0 ⇔ X(e^j(ω-ω0))

x[n] e^jω5 ⇔ X(e^j(ω-5))

3. x₃[n]= aⁿu[n]

X(e^jω)=
, gdzie |a|<1 - w-nek istnienia X(e^jω)

4. x₄[n]=nx[n], z twierdzenia o różniczkowaniu względem częstotliwości

nx[n]⇔ j

Energię każdego z sygnałów można obliczyć korzystając z twierdzenia Parsevala

E=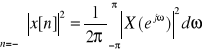

E47. Oblicz charakterystykę amplitudowo-fazową i odpowiedź impulsową systemu opisanego równaniem różnicowym y[n]=0.9y[n-1]+x[n]-5x[n-1].

;

;

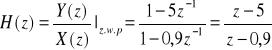
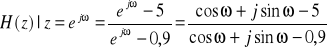
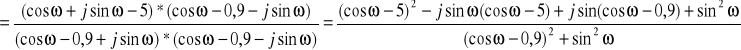
charakterystyka fazowa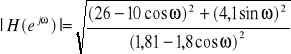

charakterystyka fazowa

E48. Zdefiniuj przekształcenie Z i oblicz Z-transformaty ciągów: a) x₁[n] = δ[n], b) x₂[n] = x[n-n₀], n i n₀ całkowite, c) x₃[n] = u[n], d) x₄[n] = aⁿu[n]. Podaj odpowiednie obszary zbieżności.

-dwustronna
-jednostronna

1. 
   ,
   ;
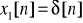
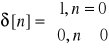
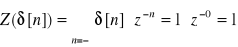
   , ROC - wszystkie z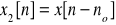

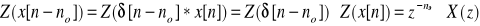
2. 
   ;
   ,

ROC - gdy n_o>0 to takie jak dla X(z) z wyjątkiem 0, gdy n_o<0 to takie jak dla X(z) z wyjątkiem nieskończoności.

3. 
   ;
   

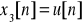
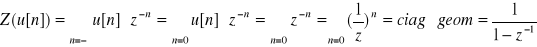
ROC: |q|<1 → (1/|z|<1) → |z|>1

4. 
   ;
   

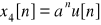
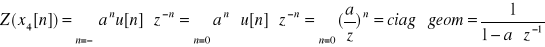
ROC: |q|<1 → (|a| / |z|) < 1 → |z| > |a|

E49.Przytocz zapamiętane właściwości przekształcenia Z.

ax₁[n]+bx₂[n]↔ aX₁(z)+bX₂(z)

x[n-1]↔ z^-1·X(z)+x[-1]

x[n-k]↔ z^-1·X(z)+ _n-1∑ⁿ x[-1]·z^-k+n

x[n-k]·u[n-k] ↔ z^-k·X(z)

x[n+1]↔ z·X(z) +x[0]

aⁿ·x[n]↔ X(z/a) dla | z | > | a |

n'·x[n]↔ -z ·dx(τ)/dt

x₁[n]·x₂[n]↔ X₁(z)·X₂(z)

E50. Oblicz oryginał x[n], gdy dana jest transformata:

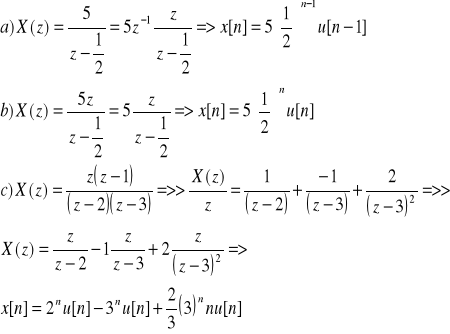
E51.Jak definiujemy transmitancje H(z) systemu DLS?

Def. H(z)=Y(z)/X(z) przy z.w.p. gdzie:x[n] →X (z); y[n] →Y(z);

h[n] →H(z) stąd H(z)=Z{h[n]}= _h=-∞ ∑ ^∞h[n] ·z ^-n
Warto wiedzieć że dla zadanej H(z) odpowiedź y[n] na x[n] dla systemu DLS przy z.w.p. obliczamy: y[n]=Z^-1 {H(z)·X(z)}

E52. Zdefiniuj warunki przyczynowości i stabilności systemu DLS o transmitancji H(z):

Transmitancja H(z):

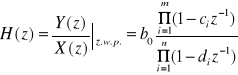
(po faktoryzacji)

gdzie: c_i -zera transmitancji ; d_i - bieguny transmitancji

• Przyczynowość

System nazywamy przyczynowym, jeśli każda próbka jego odpowiedzi zależy tyko i wyłącznie od poprzedzających ją próbek wymuszenia. Jeśli system o transmitancji H(z) jest przyczynowy to:

H[n]<0, dla n<0

i obszar zbieżności ROC jego transmitancji leży na zewnątrz bieguna d_i o największym promieniu.

• Stabilność

System nazywamy stabilnym wtedy i tylko wtedy gdy ograniczony ciąg wejściowy daje w odpowiedzi także ciąg ograniczony. Jeśli odpowiedź impulsowa h[n] systemu jest bezwzględnie sumowalna to jest on systemem stabilnym:

Obszar zbieżności ROC stabilnego i przyczynowego systemu H(z) zawiera okrąg jednostkowy. Wszystkie bieguny d_i takiego systemu leżą wewnątrz okręgu jednostkowego, tzn:
, i=1,...,m

Np.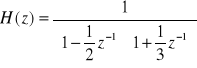

System FIR jest zawsze stabilny (w odróżnieniu od IIR).

E53. Objaśnić jak zbadać, czy przyczynowy system DLS jest stabilny. Pokaż, czy stabilny jest system o transmitancji H(z) = 1/[(z - 1/8)*(z - ¼)*(z - ½)*(z - 1)]

Jeżeli nie jest stabilny to co należałoby zmienić żeby był stabilny? Odp. Uzasadnij.

ROC stabilnego, przyczynowego systemu H(z) zawiera okrąg jednostkowy. Wszystkie bieguny d_i takiego systemu leżą wewnątrz okręgu jednostkowego tzn. | d_i | < 1, i = 1, … ,n.

H(z) = 1/[(z - 1/8)*(z - ¼)*(z - ½)*(z - 1)]

Bieguny: d₁ = 1/8, d₂ = ¼, d₃ = ½ d₄ = 1

System nie jest stabilny, gdyż biegun d₄ nie leży wewnątrz okręgu jednostkowego.

Żeby był stabilny trzeba biegun d₄ przesunąć w lewo aby znalazł się wewnątrz

okręgu jednostkowego.

E54. Czy stabilne są następujące, przyczynowe systemy DLS:

a)

ponieważ jest to transmitancja FIR'u od razu można stwierdzić iż jest to układ stabilny

!!! ”system FIR jest zawsze stabilny ” !!!

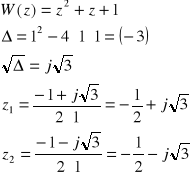
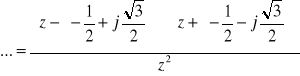
zera: ... nieważne [położenie zer nie stanowi o stabilności układu]

bieguny: 0 (podwójny)

• ROC stabilnego przyczynowego systemu H(z) zawiera okrąg jednostkowy.

• Wszystkie bieguny
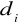
  takiego systemu leżą WEWNĄTRZ OKRĘGU

• jak bieguny leżą na okręgu to system jest NIESTABILNY!!!

Ponieważ 0 < 1 to układ jest stabilny

b)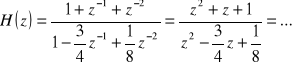

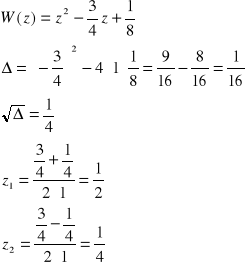
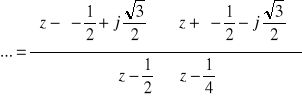
zera: ...

bieguny:

ponieważ
i
(bieguny znajdują się wewnątrz okręgu jednostkowego) to układ JEST STABILNY.

E55.Zapisz ogólne transmisje systemów DLS: IIR i FIR, i objaśnij znaczenie występujących w nich symboli.

-system IIR H(z)=Y(z)/X(z) {przy z.w.p.}=( b₀+b_1·z^-1+...+b_M·z^-M )/(1+a_1·z^-1+...+a_M·z^-M) gdzie: M-rząd systemu

-system FIR H(z)=b₀+b₁z^-1+.....b_Mz^-M = _N=0∑^M h[n]·z^-N

gdzie: Y(z)- transformata z odpowiedzi; X(z)-transformata z pobudzenia, a_i b_{i -}współ. wielomianu( współ. w równaniu różnicowym układu, jako odpowiednie wzmocnienia)

E56. Jakimi sposobami można obliczyć odpowiedź systemu DLS na dowolne pobudzenie, przy zerowych warunkach początkowych?

-na dwa sposoby(a,b): 1)odp. y[n] systemu DLS na dowolne pobudzenie x[n] jest splotem dyskretnym ciągów: pobudzenia x[n] i odp. impulsowej h[n]. Splot dyskretny jest przemienny- a)y[n]=x[n]*h[n]=h[n]*x[n]=Σ(od k=-∞ do +∞) x[k] h[n-k]= Σ(od k=-∞ do +∞) h[k] x[n-k]; 2)transmitancja systemu DLS: H(z)=Y(z)/X(z) przy z.w.p., gdzie x[n]↔X(z), y[n]↔Y(z); ponieważ: h[n]↔H(z) tzn. H(z)=Z{h[n]}= Σ(od n=-∞ do +∞) h[n]z^(-n); czyli dla zadanej H(z): b)y[n]=Z^(-1){X(Z) H(Z)}

E57. Zdefiniuj elementy schematu blokowego systemu DLS. Narysuj schematy blokowe: a) Systemu opóźniającego, b) systemu pierwszej różnicy wstecz, c) akumulatora.

DLS - dyskretny, liniowy, stacjonarny

x[n] y[n] y[n] = T{x[n]}

a) system opozniajacy y[n] = T{x[n]} = x[n-n₀]

x[n] x[n-n₀]

H(z) = z^-n0

b) system pierwszej różnicy wstecz y[n] = x[n] - x[n-1]

Dyferator

x[n] y[n]

x[n-1]

c) akumulator y[n] =
= y[n-1] + x[n]

x[n] y[n]

y[n-1]

E58. Narysuj schematy blokowe systemu IIR pierwszego rzędu i drugiego rzędu: a) strukturę bezpośrednią 1D i b) strukturę bezpośrednią 2D i zapisz ich algorytm.

System IIR :

y[n] =
bi [ n-i ] -
a_i y [n - i ]

m - rząd systemu

a) pierwszego rzędu IIR => m=1

H(z) = Y(z) / X(z) | _zwp = (b₀ + b₁z^-1) / ( 1 + a₁ z^-1)

Algorytm:

Y[n] = b₀ x[n] + b₁ x[n - 1] - a₁ y [n-1]

Schemat blokowy:

b) drugiego rzędu IIR => m=2

H(z) = Y(z) / X(z) | _zwp = (b₀ + b₁z^(-1) + b₂ z^(-2)) / ( 1 + a₁ z^(-1) + a₂ z^(-2))

Algorytm:

Y[n] = b₀ x[n] + b₁ x[n - 1] + b₂ x[n - 2] - a₁ y [n-1] - a₂ y [n-2]

Schemat blkowy

E59. Zdefiniuj DFT i przekształcenie do niego odwrotne.

DFT- dyskretne przekształcenie Fouriera; definiowane tylko dla ciągów o skończonej długości:{x[n]}(od n=0 do n=N-1), gdzie N- skończona długość; definicja DFT: X[k]= Σ(od n=0 do N-1) x[n]e^(-j2Πkn/N), dla k=0,1,…N-1; definicja przekształcenia odwrotnego do DFT (IDFT): x[n]= 1/N Σ(od n=0 do N-1) X[k]e^(j2Πkn/N), dla n=0,1,…,N-1;

E60. Jakie zachodza zwiazki pomiedzy DFT,DTFT i transformata Z przyczynowego ciagu x[n] przy zalozeniu, ze obszar zbieznosci X(z) zawiera okrag jednostkowy

E61.Wypisz i nazwij zapamiętane właściwości DFT.

-liniowość (oba ciągi o tej samej dł., w przeciwnym razie konieczność uzupełnienia zerami) ax[n]+by[n]→ aX[k]+bY[k]

-przesunięcie kołowe w dziedzinie n (n_0<0 opóźnienie całkowite) x[n+n₀] _N→ X[k]W _N ^-kno

-modulacja x[n] W _N ^kno→ X[[k+k₀ ]]_N

-splot kołowy w dziedzinie n _n=0∑^N-1 x[m] ·y[[n-m]]_N → X[k] ·Y[k]

-mnożenie w dziedzinie czasu x[n] ·y[n] → 1/N _l=0∑^N-1 X[l] ·Y[k-l]_N

-sprzężenie x*[n] → x*[[-k]]_N -sprzężenie i obrót x*[[-n]]_N→ X*[k]

-symetria x[n] → N·x[[-k]]_N

-związek Parsevala _l=0∑^N-1 ׀x[n]׀² = 1/N _k=0∑^N-1 ׀x[k]׀²

E62. Czym roznia sie widma ciag x[n] obliczone za pomoca DTFT i DFT? Pokaz na dowolnym przykladzie

E63 Objasnij zastosoawnie notacji macierzowej w obliczaniu DFT. Mozesz posluzyc sie przykladem.

E65. Na czym polega szybki splot i kiedy warto go stosować?

Splot kołowy (szybki) za pośrednictwem DFT można wykorzystać do obliczeń splotu liniowego. Stosuje się go gdy liczba próbek jest większa niż 32 (próbki zespolone) lub 64 (próbki rzeczywiste).

R1. Podać znane Ci metody zobrazowania analogowego sygnału zespolonego

a) interpretacja geometryczna, graficzna, czyli zobrazowanie sygnału zespolonego na:

- dwa wykresy (w jednakowej skali) obu składowych kartezjańskich x(t)=re u(t) i y(t)=im u(t)

- wykres dwuwymiarowy (2D) na płaszczyźnie zespolonej (płaszczyźnie Arganda) = trajektoria zespolona; wymaga dodatkowego skalowania w czasie

- wykres trójwymiarowy (3D) - spirala wije się wokół osi t

b) sygnał zespolony u(t) zdefiniowany w postaci algebraicznej można wyrażać w postaci trygonometrycznej/biegunowej (we współrzędnych biegunowych):

u(t)=a(t)exp(jφ(t)); a≥0 oraz

R2. Na czym polega faktoryzacja biegunowa sygnału zespolonego w dziedzinie czasu.

Faktoryzacja biegunowa sygnału zespolonego
; γ(t) to faktor-wskaz (o jednostkowej amplitudzie).

Po stronie częstotliwości:
, * to symbol operacji splotu.

Fazor sygnału zespolonego: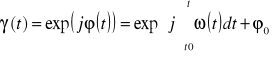
, reprezentuje cechy/atrybuty strukturalne sygnału u(t), takie jak jego „szybkość kątowa”/pulsację chwilową ω(t) i orientację/fazę początkową φ₀.

R3. Zdefiniować amplitudę chwilową, fazę chwilową i pulsację chwilową danego sygnału zespolonego.

Amplituda chwilowa - jest wartością bezwzględną (modułem) zespolonej wartości chwilowej:
. Przebieg amplitudy chwilowej często nazywa się obwiednią przebiegów rzeczywistych, zarówno x(t) jak i y(t), gdyż -a(t)≤x(t),y(t)≤a(t)

Faza chwilowa - argument (część urojona) zespolonego logarytmu funkcji zespolonej u(t) zmiennej rzeczywistej t:
.

W powyższej definicji fazy chwilowej zarówno arg jak i ln są operatorami (nie funkcjami „bezinercyjnymi” jak np. |( )|, czy exp( )) zdefiniowanymi przez Cauchy'ego jako arg≡im ln oraz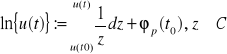

Pulsacja chwilowa sygnału u(t) to pochodna jego fazy chwilowej φ(t) względem czasu t:
. Korzystając z definicji fazy chwilowej otrzymujemy: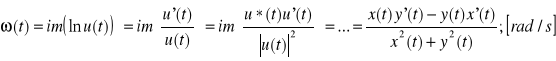

R4. Na czym polega rozwijanie fazy zespolonej sygnału analogowego? Kiedy lub po co jest ona stosowana?

Fazę chwilową obliczoną trygonometrycznie/cyklometrycznie ze wzoru:
, nazywamy główną lub zwiniętą w odróżnieniu od fazy rozwiniętej obliczanej według wzoru:

Przedział
. Przedział
nazywa się zwojem (lub okresem) głównym fazy funkcji określonej ex(jφ). Faza rozwinięta φ(t) i faza główna φ_P(t) są powiązane wzorem:

Obliczanie φ(t) w oparciu φ_P(t) nazywa się rozwijaniem fazy, a odwrotnie: φ_P(t) w oparciu o φ(t) - zwijanie fazy.

R5. Moc chwilowa i twierdzenie Parsevala dla sygnałów analogowych zespolonych. Energia sygnału zespolonego.

Moc chwilowa sygnału zespolonego u(t):

Energia (całkowita) sygnału zespolonego: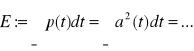
może być skończona albo nieskończona. Z tego wywodzą się dwie klasy sygnałów analogowych:

- o skończonej energii:

- o skończonej mocy (chwilowej):

Równość Parsevala dla sygnałów zespolonych:

, ale też:

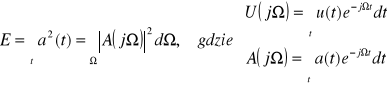
R6. Zinterpretować sygnał zespolony na płaszczyźnie zespolonej Arganda
DIAGRAM ARGANDA

Diagram Arganda jest przedstawia liczby zespolone jako punkty

z=x+jy

oś iksów jako oś części rzeczywistej i oś igreków jako oś części zespolonej

na wykresie powyżej przerywany okrąg reprezentuje zespolony moduł |z| liczby `z'

a kąt
reprezentuje jej zespolony argument

Diagram Argand'a tak naprawdę został wymyślony wcześniej przez C.Wessel'a

R7. Omówić znane Ci reprezentacje biegunowe sygnału x(t)+jy(t); x(t), y(t)
R

Kartezjańska reprezentacja sygnału x(t): u(t)=x(t)+jy(t)
równoważnik (sygnału) analityczny

Biegunowe reprezentacje sygnału x(t):

(AM - modulacja amplitudy, FM - modulacja częstotliwości)

zespolona reprezentacja dynamiczna

log obwiednia, poziom chwilowy [dB]

pulsacja chwilowa,
- częstotliwość chwilowa

zespolona pulsacja chwilowa

(PM - modulacja fazy)

zespolona faza chwilowa

”zapis nutowy”;
wysokość chwilowa (instantaneous pitch), gdy p=2 mianowana w oktawach, gdy p=2^1/12 - w półtonach

R8. Omówić główne (kluczowe) właściwości reprezentacji biegunowych

1. mnożenie (wartości chwilowych) przebiegów zespolonych skutkuje mnożeniem ich amplitud chwilowych oraz dodawaniem ich faz chwilowych i pulsacji chwilowych

2. niech a(t), ϕ(t) i ω(t) są odpowiednio amplitudą chwilową, fazą chwilową i pulsacją chwilową przebiegu zespolonego, to:

• amplituda chwilowa, faza chwilowa i pulsacja chwilowa przebiegu zespolonego sprzężonego u*(t) wynoszą odpowiednio: a(t), - ϕ(t) i - ω(t)

• amplituda chwilowa, faza chwilowa i pulsacja chwilowa przebiegu przeskalowanego w czasie u(αt); α≠0 ∈R, wynoszą odpowiednio: a(αt), ϕ(αt) i αω(t)

R9.Amplituda chwilowa, faza chwilowa i pulsacja chwilowa analogowego sygnału rzeczywistego - postulaty Valkmana

Amplituda chwilowa (obwiednia), faza i pulsacja chwilowa sygnału rzeczywistych muszą spełniać trzy postulaty Valkmana, które spełniają amplituda chwilowa, faza i pulsacja sygnałów zespolonych.

1. Małe zmiany w przebiegu wartości chwilowych sygnałów rzeczywistego x(t), co zapisujemy jako: x(t) + δx(t), powinny powodować również małe zmiany w przebiegu jego amplitudy chwilowej (obwiedni) a(t), co zapisujemy jako

Obwiednia {x(t) + δx(t)} ⇒ obwiednia {x(t)}, gdy {δx(t)} 

2. Faza i częstotliwość chwilowa powinny być niezależne od wielkości skali/sygnału

∀c≠0 ∈R faza chwilowa {cx(t)} = faza chwilowa{x(t)}

3. Amplituda chwilowa, faza chwilowa i pulsacja chwilowa ”czystej” sinusoidy rzeczywistej (a₀≠0, ω₀>0)

a₀cos(ω₀t + ϕ₀) powinny być równe parametrom tej sinusoidy

amplituda chwilowa {a₀cos(ω₀t + ϕ₀)} = a₀

faza chwilowa {a₀cos(ω₀t + ϕ₀)} = ω₀t + ϕ₀

pulsacja chwilowa {a₀cos(ω₀t + ϕ₀)} = ω₀

R10. Amplituda chwilowa, faza chwilowa i pulsacja chwilowa analogowego sygnału rzeczywistego - koncepcja Gabora - Ville (klasyczna)

Koncepcja utworzenia sygnału analitycznego u(t) z sygnału rzeczywistego x(t) poprzez usunięcie „połowy widma” X(jΩ) zajmującego ujemna półoś jΩ wywodzi się z możliwości (czy chęci)m dwukrotnej redukcji „nadmiarowości widmowej” sygnału rzeczywistego x(t), którego widmo jest Hermitowsko symetryczne/parzyste: X(-jΩ)= X*(jΩ). Wzmocnienie dwukrotne widma pozostawionego na dodatniej półosi jΩ ma zapewnić równość mocy i energii danego sygnału rzeczywistego x(t) i jego równoważnika zespolonego u(t) oraz to, by x(t) pozostał częscią rzeczywistą u(t), czyli

x(t)=Reu(t) ⇔_F X(jΩ) = (U(jΩ) + U*(-jΩ))/2, F - oznacza parę transformat Fouriera

Jedynym sygnałem zespolonym, który w taki (liniowy) sposób jest związany z danym sygnałem rzeczywistym x(t) jest sygnał u(t) którego widmo

U(jΩ)=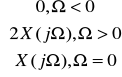

i który Gabor nazwał sygnałem analitycznym a Ville - preobwiednią (preenvelope). Część urojona sygnału x(t) spełnia oczywistą zależność

y(t)=Imu(t) ⇔_F Y(jΩ) = (U(jΩ) - U*(-jΩ))/(2j)

R11.Zdefiniować (w dziedzinie czasu i w dziedzinie częstotliwości) przekształcenie Hilberta i operator wykonujący to przekształcenie.

y(t) = CPV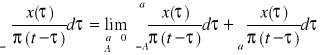
, 0<a<A<∞

CPV- wartość główna Cauchy'ego

W wyniku całkowania otrzymamy przebieg y(t) nazwany transformatą Hilberta przebiegu x(t). Transformata Hilberta danego przebiegu x(t) powstaje w wyniku filtracji lilniowej splotu liniowego danego przebiegu x(t) z odpowiedzią impulsową

h_T(t)=

Nieprzyczynowy o zerowym opóźnieniu filtr H_T o podwyższonej odpowiedzi impulsowej charakterystyce częstotliwościowej

H_T(j2πF) = -jsign(F); F=
nazywamy transformatorem Hilberta.

R12. Omówić własności par transformat Hilberta i sygnałów analitycznych

Własności pary transformat Hilberta = właściwości składowych sygnału analitycznego = właściwości zespolonego równoważnika x(t)+jy(t) sygnału rzeczywistego x(t) wynikają m. in. z faktu, że H_T^-1=-H_T=H_T*.

1. transformator Hilberta nie przenosi składowej stałej

2. Jeśli y(t)=HT{x(t)}, to H_T^-1{y(t)}=
   

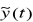
Gdzie
<=składowa zmienna sygnału y(t)

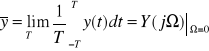
<= składowa stała, centroid (wartość średnia) y(t)

3. dwukrotne przejście przebiegu x(t) przez transformator Hilberta H_T (=przejście przez kaskadę dwóch transformatorów Hilberta H_TH_T) zmienia znak sygnału na przeciwny (i usuwa z niego część stałą), czyli H_TH_T^-1{x(t)}=
   

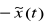
4. Widma: amplitudowe, mocy/energii i opóźnienia grupowego przebiegów x(t) i y(t) są identyczne za wyjątkiem częstotliwości F=0

5. Widma fazowe przebiegów x(t) i y(t) różnią się o π/2 (90^o) => przebiegi x(t) i y(t) są ortogonalne

6. Niech x(t)=x_e(t)+x_o(t), gdzie:

x_e(t):=(x(t)+x(-t))/2 <= składowa parzysta,

x_o(t):=(x(t)-x(-t))/2 <= składowa nieparzysta prebiegu x(t),

Niech y(t)=H_T{x(t)}=y_e(t)+y_o(t). Wtedy H_T{x_e(t)}=y_o(t) i H_T{x_e(t)}=y_e(t)

7. Twierdzenie Bedrosiana: Niech x(t)=a(t)*b(t) przy czym widma czynników a(t) i b(t) nie zachodzą na siebie (co można zapisać jako A(jΩ)B(jΩ)=0 ∀Ω∈(-∞;+∞)), wtedy y(t)=H_T{a(t)b(t)}=a(t)H_T{b(t)}=b(t)H_T{a(t)}

8. Trajektoria sygnału analitycznego x(t)+jy(t) „jest dodatnioskrętna”, czyli zarówno lokalnie (wokół chwilowego środka krzywizny) jak i globalnie (wokół „środka ciężkości” = centroid ) wije się w kierunku dodatnim.

R13. Zdefiniować podstawowe parametry analogowego sygnału pasmowego (rzeczywistego i zespolonego): pasmo, szerokość pasma, częstotliwość środkowa.

• Sygnał rzeczywisty

To F=0 jest częstotliwością środkową sygnału podstawowo pasmowego: FC=0, a szerokość pasma jest równa podwójnej górnej częstotliwości granicznej B=2F_u

• Sygnał zespolony

Zdefiniowany jako w(t)= exp(-2jπF_C) * H_A {x(t)} =2H_LP {exp (-2jπF_C) * x(t)}

Gdzie :

H_A - zespolony filtr Hilberta

H _LP - filtr dolnoprzepustowy o paśmie przepustowym (-B/2, B/2) i paśmie zaporowym powyżej 2F_C-B/2

R14. Zdefiniować obwiednię zespoloną rzeczywistego sygnału pasmowego.

Definicja obwiedni:

w(t)=exp(-2jπF_C) * H_A {x(t)} =2H_LP {exp (-2jπF_C) * x(t)}

R15. Omówić własności obwiedni zespolonej.

Zdefiniowany wyżej sygnał w(t) nazywa się obwiednią zespoloną sygnału rzeczywistego x(t) pasmowego / wąskopasmowego.

Obwiednia zespolona:

w(t)=i(t)+jq(t) ; i(t), q(t)∈R

jest podstawową kartezjańską reprezentacją zespoloną sygnału x(t) o najniższej częstotliwości granicznej F_U=B/2, F_L(w)=-B/2.

Składowe kartezjańskie obwiedni zespolonej nazywają się odpowiednio:

• i(t)=re w(t) - składowa synfazowa

• q(t)=im w(t) - składowa kwadraturowa, z tego powodu obwiednia zespolona jest czasem nazywana reprezentacją i/q lub parą kwadratur podstawowopasmowych.

38

T{
}

x[n]

y[n]

T{
}

x[n]

y[n]

y[n]

n

0

1

2

3

4

5

6

7

x[n]

n

0

1

2

3

4

h₂[n]

h₁[n]

h₁[n]

h₂[n]

.3 2 1

x 1 .2 3

9 6 3

6 4 2

+3 2 1

3 .8 14 8 3

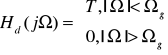
Arctgx(
)

Arctg(0,5)

T{•}

z^-n0

+

z^-1

z^-1

+

y[n]

+

+

z^-1

x[n]

b₀

-a₁

b₁

y[n]

x[n]

+

+

+

+

z^-2

z^-1

-a₁

-a₂

b₂

b₁

b₀

---