CZĘŚĆ PIERWSZA PODSTAWY TEORII RUCHU POCIĄGU

Rozdział 1

ELEMENTARNA TEORIA KOŁA TRAKCYJNEGO

1.1. Walcowy model koła [10].

Walcowe koło trakcyjne, ogólnie odkształcalne, w polu grawitacyjnym toczy się po ogólnie nierównej nawierzchni, której nierówności są znikomo małe w stosunku do promienia tego koła. Pomiędzy kołem trakcyjnym a nawierzchnią występuje, normalne do powierzchni styku tych dwóch brył, dynamiczne oddziaływanie wzajemne Q(t). Wywiązywanie stycznej do nominalnego okręgu koła siły trakcyjnej F(t) jest fizycznie możliwe dzięki siłom przyczepności występującym na powierzchni styku brył. Na bryłę koła działa zewnętrzny trakcyjny moment napędowy M(t), wektor równoległy do osi koła, który jest równoważony przez parę przeciwnie skierowanych sił trakcyjnych F(t), rozmieszczonych na odległości określonej przez trakcyjny promień koła R_t(M). Środek S koła porusza się z prędkością
względem nawierzchni. W nieskończenie krótkim przedziale czasu dt możemy traktować zjawisko jako elementarny proces chwilowo ustalony.

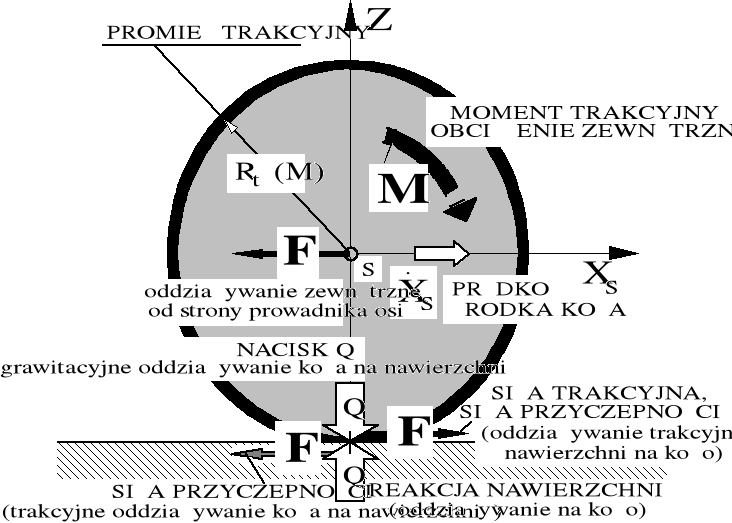
Rysunek 1.1. Elementarna równowaga walcowego modelu koła podczas ruchu trakcyjnego.

Koło kolejowe nie może być traktowane jako walcowe. Zrozumienie teorii jego współpracy z szyną oraz fizycznej istoty poszczególnych składowych oporu ruchu kolejowego koła po szynie wymaga rozpatrzenia kilku przypadków szczególnych.

1.2. Przypadek szczególny zakrzywionej linii styku dwóch doskonale sztywnych, tocznie współpracujących elementów, bez wywiązywania sił trakcyjnych [10].

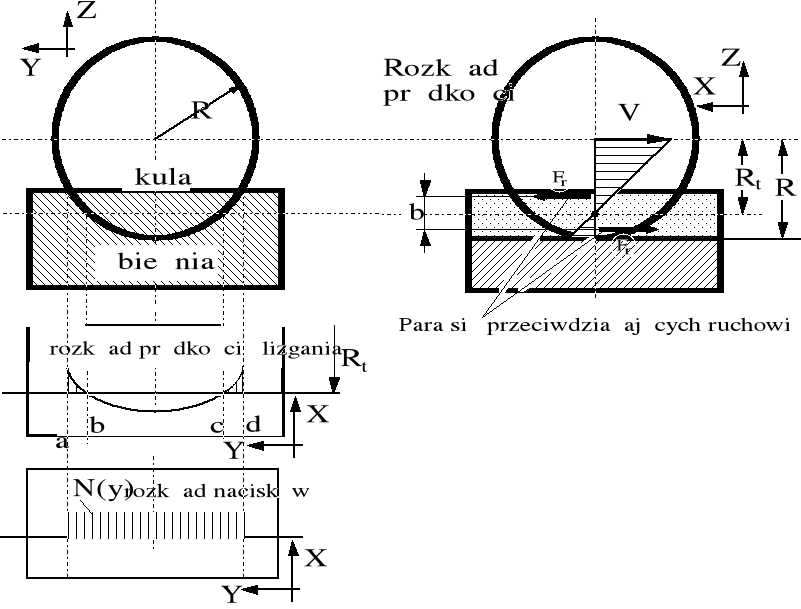
Przedstawiona na rysunku 2 toczna współpraca dwóch brył dobrze ilustruje pojęcie promienia kinematycznego R_t. Wartość tego promienia wynika z dynamicznych warunków poślizgowej współpracy brył na kierunku ruchu.

Wszystkie elementarne siły tarcia
działające na kierunku x linii styku (jest to kierunek ruchu koła), muszą pozostawać we wzajemnej równowadze w „pionowych” strefach linii kontaktu brył R>R_t oraz R≤R_t.

Warunek równowagi statycznej sił podłużnych na kierunku ruchu x:

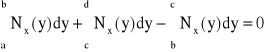
(1.1a)

oraz warunek równowagi momentów względem osi obrotu na kierunku y:

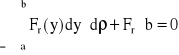
(1.1b)

Siły tarcia wywiązują się w obrębie zakrzywionej linii styku doskonale sztywnego materiału koła i bieżni poprzez parę wypadkowych sił tarcia F_r zgodnie z rysunkiem 2. Styczna do osi kanałka bieżni wartość wypadkowej w określonym kierunku siły tarcia F_T torusu koła (lub kuli) poruszającego się w rowku wynosi:

Podobne warunki równowagi można napisać dla przypadku ruchu z siłami trakcyjnymi. W przypadku występowania sił trakcyjnych promień równowagi kinematycznej współpracy koła z nawierzchnią będziemy nazywać promieniem trakcyjnym niezależnie od kształtu strefy ich styku. Do zagadnienia tego powrócimy ponownie w punkcie 6.

W szczególnym przypadku swobodnego toczenia się doskonale sztywnego walca po doskonale sztywnej płaszczyźnie (bez sił trakcyjnych), siła oporu F_T, według powyższego zrozumienia zjawiska, nie wystąpiłaby gdyż R_t=R.

1.3. Przypadek quasi-prostokątnej strefy styku elementów sprężysto - plastycznych: walca i płaszczyzny. Podstawowa składowa oporu swobodnego toczenia się kolejowych kół po szynach [13].

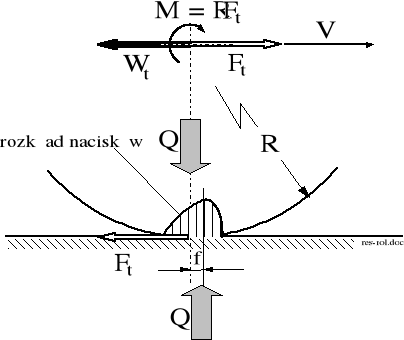
Rysunek 1.3. Bilans równowagi trakcyjnego momentu napędowego M, nacisku walcowego modelu koła na płaską szynę Q oraz reakcji szyny Q na koło przy toczeniu się sprężysto - plastycznego koła po sprężysto - plastycznej nawierzchni kolejowej.

Ft - czynna (styczna) siła trakcyjna;

Wt - opór ruchu (trakcyjna reakcja) koła;

R - promień fizyczny koła;

Q - nacisk koła na szynę.

Podczas toczenia się koła po szynie, w wyniku wewnątrz materiałowej histerezy, towarzyszącej zmiennym w czasie odkształceniom poszczególnych sprężysto - plastycznych cząsteczek materiału w strefie styku, rozkład nacisków asymetryzuje się zgodnie z rysunkiem 3.

Moment oporu ruchu M_t toczenia się koła po szynie (nie pokazany na rysunku) wynosi:

(1.2)

gdzie: Q - nacisk koła na szynę, f - dynamiczne przesunięcie osi reakcji w stosunku do siły nacisku, W_t - opór ruchu koła wywołany toczeniem się koła po nawierzchni.

Wielkość f jest niekiedy nazywana współczynnikiem tarcia tocznego. W praktyce kolejnictwa f ≤ 5⋅10^-4 [m] i praktycznie nie zależy od prędkości V ruchu koła. Wielkość ta odpowiada walcowemu modelowi koła rzeczywistego współpracującego z płaską, poziomą belką szyny rzeczywistej.

1.4. Przypadek quasi-eliptycznej strefy styku elementów sprężysto plastycznych: techniczna ilustracja pojęcia spinu - kula w rowku [10].

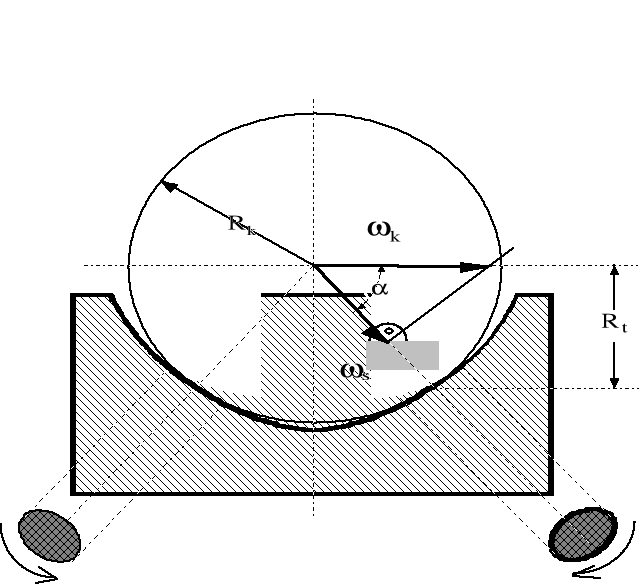
Rysunek 1.4. Poślizg wiertny, czyli spin podczas ruchu kuli w kanałku w warunkach styku dwupunktowego.

Podczas ruchu środka kuli z prędkością
w kanałku jej prędkość kątowa wynosi:

(1.3)

Zgodnie z rysunkiem 1.4 prędkość kątowa poślizgu wiertnego (spinu) wynosi

(1.4)

W kole walcowym, prosto toczącym się po płaszczyźnie, spin nie występuje.

1.5. Poślizg wiertny (spin) kolejowo uprofilowanego koła i związany z tym opór ruchu swobodnego (bez sił trakcyjnych) [10].

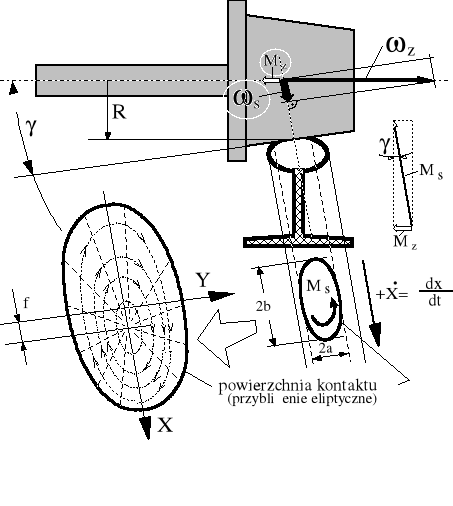
Rysunek 1.5. Ilustracja poślizgu wiertnego (spinu) kolejowego koła na szynie.

z - prędkość kątowa zestawu;

s - prędkość spinu.

(1.5)

Jako Ms oznaczono na rysunku moment reakcyjny spinu (działający w bezpośredniej strefie styku koła i szyny na kolejowo uprofilowane koło), określający opór ruchu Ws, pochodzący tylko od spinu. Moment M_s jest bardzo trudny do zmierzenia. Dlatego posługujemy się odpowiednio przeliczonym, łatwym do zmierzenia momentem M_z, którego wektor leży w osi koła:

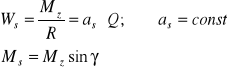
(1.6)

Ponieważ uogólniona siła tarcia suchego zależy jedynie od wartości nacisku normalnego i od współczynnika tarcia, lecz praktycznie nie zależy od prędkości poślizgu, przeto w uproszczonym modelu tarcia wiertnego przyjęto podobnie, że (stosunkowo niewielka) składowa dodatkowego oporu ruchu toczenia się stożkowego koła zestawu po szynie z dobrym przybliżeniem zależy od pionowego nacisku koła na szynę oraz od wartości stałego współczynnika proporcjonalności a_s. Kąt γ jest niewielki, w praktyce zawsze mniejszy od 0,06 [rad]. Opór spinu W_s wyraża się więc następującym wzorem:

(1.7)

1.6. Ruch trakcyjny walcowego modelu koła napędzającego oraz hamującego na płaszczyźnie. Pojęcie promienia trakcyjnego. Trakcyjny poślizg koła.

W badaniach dynamiki trakcyjnej współpracy koła z nawierzchnią posługujemy się pojęciem poślizgu wzdłużnego definiowanego poprzez prędkości: obwodową R (na obwodzie koła) i prędkość ruchu postępowego
(środka koła).

(1.8)

gdzie R - promień (geometryczny) koła.

Najprostsze jest przedstawienie związku (1.8) z wprowadzeniem abstrakcyjnego promienia trakcyjnego Rt(F), zgodnie z rysunkiem 1.5.

Toczące się po szynie koło o nominalnym promieniu geometrycznym R ma na obwodzie prędkość obwodową R; zaś koło o promieniu trakcyjnym Rt, - prędkość obwodową odpowiadającą ściśle prędkości ruchu postępowego środka koła czyli
. W istocie, napędzane i obracające się z prędkością kątową , trakcyjnie obciążone siłą FN koło o promieniu R, osiąga taką samą prędkość jazdy jaką by osiągało tocząc się bez poślizgu, gdyby miało promień trakcyjny Rt.

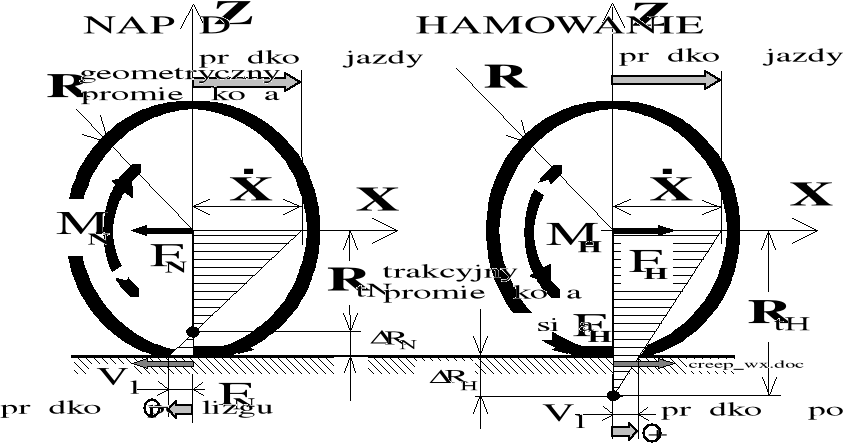
Rysunek 1.6. Ilustracja pojęcia promienia trakcyjnego dla trakcyjnych przypadków roboczych napędu i hamowania koła walcowego.

(1.9)

Wyznaczenie R jest łatwe dzięki znajomości eksperymentalnych wykresów F(Vśl) lub F() a także analitycznie, za pomocą uproszczonego wzoru Cartera:

(1.10a)

Dla modelu Cartera, zgodnie z rysunkiem 1.7, otrzymujemy:

(1.10b)

W ruchu trakcyjnie obciążonego koła po szynie, prędkość poślizgu w punkcie kontaktu koła i szyny wynosi
czyli jest określona iloczynem R:

Vśl = R;

Zgodnie z charakterystyką F(Vśl) sporządzoną na drodze eksperymentu [10], możemy napisać:

F= Vśl;

gdzie,

Opisane przez (1.9) pojęcie promienia trakcyjnego Rt zachowuje modelową ścisłość tylko dla mikropoślizgów rozumianych w sensie aproksymacyjnym (przybliżenie liniowe).

Zgodnie z badawczym ujęciem zaprezentowanym w pracy [10] mamy więc:

(1.11)

Istnieje więc łatwa możliwość eksperymentalnej identyfikacji poszczególnych wielkości we wzorach.

Przedstawiona na rysunku 1.7b krzywa przyczepności, w zrozumieniu aproksymacyjnym, przy posługiwaniu się pojęciem promienia trakcyjnego Rt, może być traktowana jako krzywa tarcia trakcyjnego.

Podobnie i konsekwentnie, współczynnik przyczepności może być traktowany jako zastępczy współczynnik tarcia trakcyjnego.

Różnica R promieni: geometrycznego R i trakcyjnego Rt, po eksperymentalnym zidentyfikowaniu może niejawnie zawierać w sobie, wiernie odwzorowany mikropoślizg rzeczywisty, pod którym kryją się wszystkie właściwości geometryczne, materiałowe i trybologiczne koła i szyny. Przyjęta metoda aproksymacji procesu poślizgu, po uwzględnieniu fizycznych ograniczeń na szczytowe wartości sił przyczepności, jest dostatecznie ścisła dla zastosowań symulacyjnych w technice trakcyjnej. Ilustracje graficzne zmiany położenia chwilowego środka obrotu koła w zależności od stanu jego obciążenia trakcyjnego, stanowią rysunki 1.6 i 1.8.

Podczas postoju (także trakcyjnie obciążonego) koła na nawierzchni, gdy koło się nie obraca, = 0, chwilowy środek obrotu pozostaje nie uaktywniony. Podczas postoju, R(F) opisuje - według (1.10) lub (1.11), jedynie abstrakcyjny poślizg potencjalny.

W ruchu trakcyjnie obciążonego koła po szynie lub po nawierzchni drogowej, zmiana promienia R ujawnia się fizycznie i promień trakcyjny Rt może być zidentyfikowany eksperymentalnie (1.11) lub opisany przez odpowiedni model matematyczny (1.10).

Znakookreśloność parametrów: momentu (napędzającego / hamującego)

M = FR, działającego na koło zgodnie z kierunkiem jego osi, oraz [znak] prędkości V jego środka, decydują o spadku R lub przyroście wartości promienia trakcyjnego w stosunku do promienia geometrycznego R.

Należy więc wyróżnić dwa przypadki techniczne: napędzanie i hamowanie. W warunkach "napędu" promień trakcyjny jest mniejszy od promienia geometrycznego R; w warunkach "hamowania" i promień trakcyjny jest większy od R.

Wszystkie wyżej przedstawione wzory, począwszy od (8), obowiązywały wyłącznie dla technicznego przypadku przyśpieszania lub napędzania koła w ruchu ze stałą prędkością. Przy hamowaniu sytuacja jest nieco odmienna.

Dla hamowania obowiązuje następujący zapis formalny:

(1.12a)

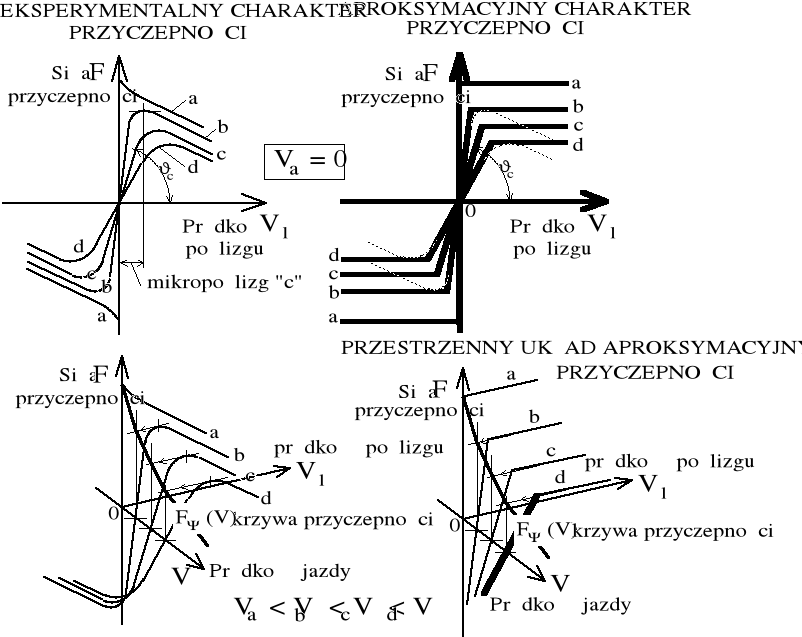
Rysunek 1.7. Charakterystyki sił przyczepności: eksperymentalne a) i b) oraz aproksymacyjne c) i d) [5], [6], [8], [9], [10].

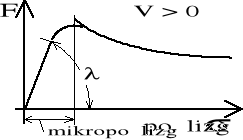
Rysunek 1.8. Charakterystyka siły przyczepności w funkcji poślizgu .

Odmienny zapis wzoru opisującego poślizg przy hamowaniu wynika tylko stąd, że przyjęto iż jest zawsze dodatnie, a jego wartość zawiera się pomiędzy zero i jeden; 0<R1.

1.7. Przyczepność koła do nawierzchni jako uogólnienie zjawiska tarcia [13], [10] [9].

Zgodnie z zakresem p. 1.6, powszechnie znane z fizyki zjawisko tarcia jest zaledwie szczególnym przypadkiem ogólniejszego zjawiska przyczepności.

Koło kolejowe, toczące się po szynie i hamowanie hamulcem klockowym, stanowi obiekt mechaniczny, w którym obydwa te zjawiska występują pojęciowo w sposób szczególnie czytelny. W przypadku ruchu koła po szynie hamowanego klockowo, zgodnie z rysunkiem 1.8, prędkość przemieszczania się koła (ściślej - środka okręgu koła) wzdłuż szyny i prędkość ślizgania się klocka po okręgu koła, są ogólnie różne od zera:
W takich warunkach ruchu (hamowanie - „H”), poślizg σ w punkcie P styku koła z szyną we wzorze (1.12a) przyjęto jako wielkość bezwymiarową opisaną stosunkiem różnicy prędkości w punkcie styku do prędkości ruchu środka okręgu koła.

(1.12b)

gdzie Φ - chwilowy kąt obrotu koła; x - współrzędna położenia środka okręgu wzdłuż toru; R - promień okręgu tocznego.

Umówiono się, że

W szczególnym przypadku
mamy do czynienia ze zjawiskiem tarcia. Zatrzymane w ruchu obrotowym podczas hamowania koło
, przemieszczając się wzdłuż szyny z prędkością chwilową
realizuje poślizg o wartości σ = 1. W takich szczególnych warunkach ruchu koła po szynie mamy do czynienia ze zjawiskiem tarcia w punkcie P.

W przypadku napędzania („N”) koła, poślizg opisuje się odpowiednio w postaci (1.8), jako stosunek różnicy prędkości w punkcie styku do prędkości mierzonej na okręgu koła.

W przypadku ruchu napędnego koła, w warunkach szczególnych
odpowiadających początkowi forsownego rozruchu, poślizg nie przekracza wartości 1, lecz ją, co najwyżej, osiąga
; oznacza to możliwość występowania zjawiska tarcia.

W punkcie P styku koła z szyną tarcie występuje jedynie w dwóch szczególnych przypadkach:

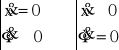
(1.13)

W przypadku ogólnym,
mamy jedynie do czynienia ze zjawiskiem przyczepności.

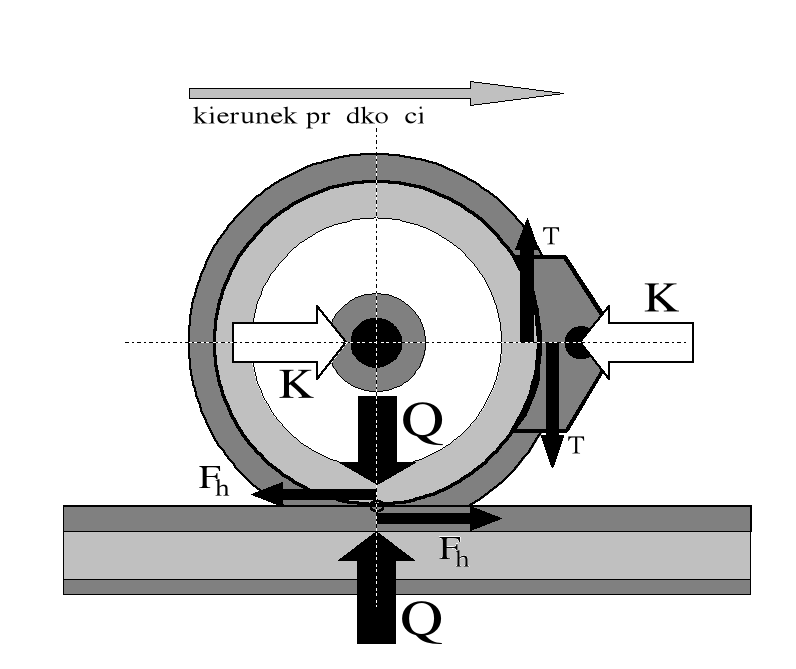
Rysunek 1.9. Zasada klockowego hamowania koła. Promień działania sił tarcia i przyczepności jest taki sam.

W punkcie T możemy rozpatrywać zjawisko styku powierzchniowego klocka z bieżnią koła. Ponieważ klocek jest zawieszony na ramie wózka i porusza się wraz z pojazdem, wzdłuż toru, z prędkością
to prędkość ślizgania pomiędzy powierzchnią toczną koła i powierzchnią roboczą klocka, występująca we wzorach (1.8) i (1.9) w liczniku, wyrazi się jako

(1.14)

W punkcie T możemy rozważać jedynie zjawisko tarcia.

Pojęciu przyczepności przyporządkowujemy pojęcie siły przyczepności F_P zaś pojęciu tarcia przyporządkowujemy pojęcie siły tarcia F_T. Biorąc pod uwagę wartości sił docisku Q i K w punktach P i T koła możemy mówić o granicznych wartościach sił przyczepności F_Pmax i tarcia F_Tmax opisanych wzorami:

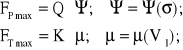
(1.15)

gdzie: Ψ - współczynnik przyczepności;

μ - współczynnik tarcia.

Ponieważ każda z sił opisanych wzorami (1.15) jest funkcją innej zmiennej, przeto bezpośrednie ich porównanie jest możliwe jedynie w przestrzeni trójwymiarowej (F, V_śl, σ), według rysunku 1.7.

W trakcji kołowej i kolejowej posługujemy się wzorami empirycznymi opisującymi zjawiska przyczepności i tarcia w funkcji prędkości jazdy bez wnikania w wartości mikro-poślizgów σ, małych w poprawnej eksploatacji. Takie podejście oznacza, że na płaszczyźnie F(V) odwzorowuje się projekcję linii grzbietowej powierzchni F(V,V_śl), zgodnie z rysunkiem 1.7b.

W kolejnictwie dość powszechnie są znane wzory Andrewsa oraz Curtiusa- Knifflera dla opisu przyczepności oraz Karwackiego dla opisu tarcia w funkcji prędkości jazdy V do wartości ok. 35 m/s:

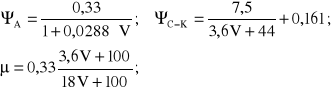
(1.16)

gdzie: prędkość V została wyrażona w [m/s], oraz przyjęto ujednoliconą wartość początkową
W praktyce eksploatacyjnej zachowujemy warunek
w związku z czym określa się współczynnik intensywności hamowania δ:

(1.17)

Współczynnik intensywności hamowania w kolejnictwie, przy wysokich prędkościach, może bezpiecznie osiągać nawet wartość 1,8.

1.8. Promień trakcyjny kolejowo uprofilowanego koła

Na mocy uwag zawartych w p.1.6 należy zauważyć, że efektywny promień trakcyjny koła kolejowego zależy od kilku czynników:

• od profilu koła kolejowego,

• od profilu szyny,

• od położenia koła względem szyny,

• od krzywizny toru kolejowego pod zestawem kół,

• od obciążeń trakcyjnych (napędowych i hamujących),

• od konstrukcyjnych i materiałowych parametrów elementów konturu adhezyjnego.

Zagadnieniu współpracy zestawu z torem zakrzywionym poświęcimy uwagę w dalszym ciągu niniejszego rozdziału.

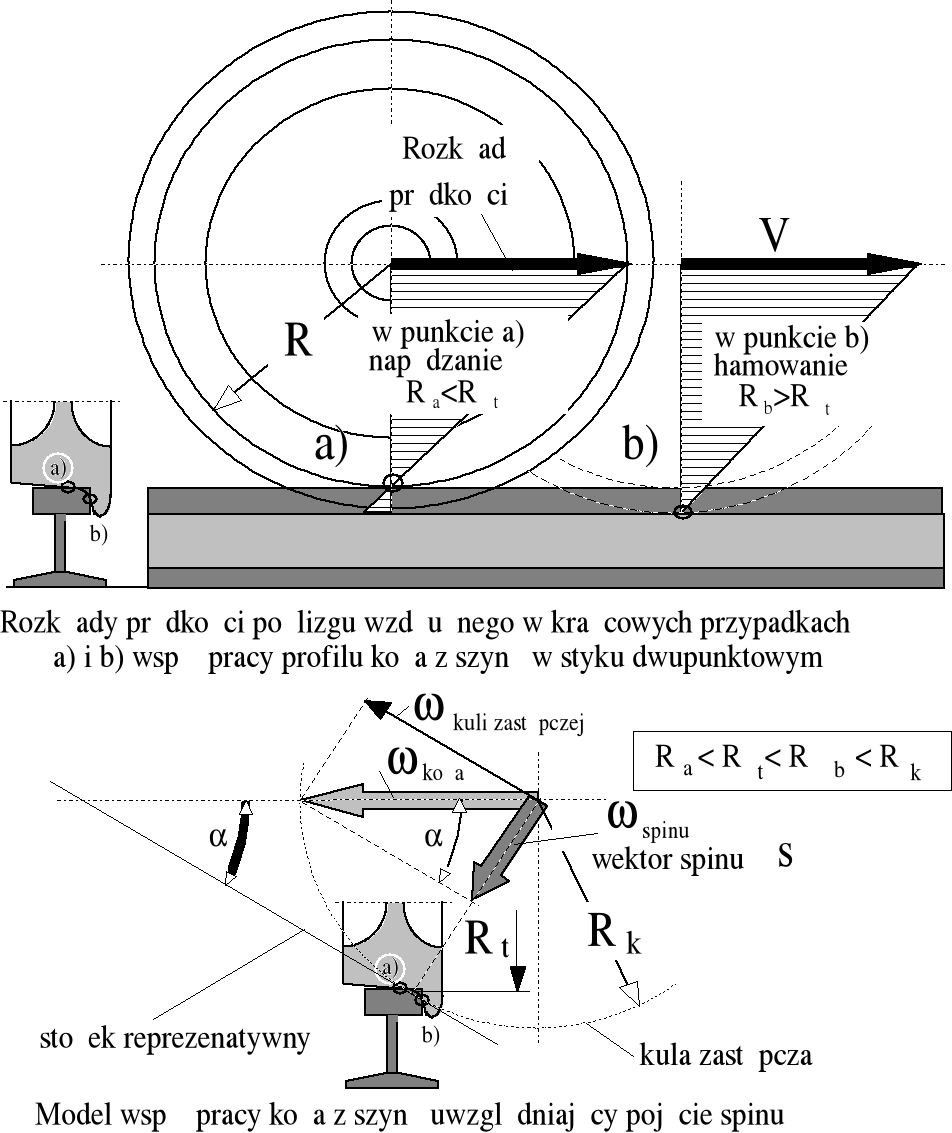
Rysunek 1.9. Ilustracja promienia trakcyjnego koła kolejowego przy jego współpracy z szyną. Pojęcie kuli zastępczej wprowadzono jedynie dla nawiązania do rysunku 1.4.

1.9. Ruch kolejowego zestawu kół w łuku toru [10].

Uprofilowany kolejowo zestaw kół jest prowadzony w torze zasadniczo za pomocą podłużnych sił przyczepności. Takie jest prawidłowe prowadzenie eksploatacyjne. Możliwość bocznego kontaktu obrzeża z główką szyny, jak pokazano na rysunku 1.9, należy traktować jedynie jako zabezpieczenie przed wykolejeniem na przykład w obrębie wejścia w ostry łuk lub rozjazd. Prowadzenie zestawu kół w torze realizuje się więc dzięki występowaniu konturu adhezyjnego z siłami przyczepności i sprężystości układu konstrukcyjnego. Kontur adhezyjny zestawu kół zilustrowano rysunkiem 1.10.

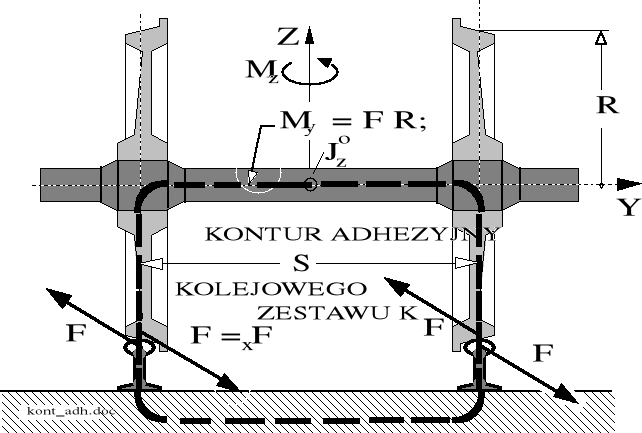
Rysunek 1.10. Ilustracja konturu adhezyjnego prowadzącego zestaw kół w torze.

Przypadek ruchu zestawu obciążonego wewnętrznym momentem konturu adhezyjnego: koło - oś zestwu - koło - tor - koło, w łuku toru (bez obciążeń trakcyjnych) dodatkowo zilustrowano rysunkiem 1.11. Rysunek 1.1 przedstawia schemat obciążenia koła w ruchu ustalonym zaś rysunek 1.10 ilustruje stan poślizgów na kołach zestawu prowadzonego radialnie w łuku o małym promieniu.

Sztywność skrętna osi zestawu tocznego o średnicy d[m] wynosi:

(1.13)

Gdzie G - moduł sprężystości postaciowej; dla stali G = 8,0851010[N/m2];

s - rozstaw okręgów tocznych (rozstaw szyn toru)

Oś, pod działaniem panującego w konturze momentu M, na całej swej długości skręca się o kąt :

(1.14)

Skręcenie to daje na obwodzie koła przyrost drogi R. Na torze prostym, uległoby ono odprężeniu po przebyciu drogi LR/R.

Stąd możemy wyznaczyć drogę kinematycznego odprężania osi:

(1.15)

Jednakże ruch w łuku wywołuje nieustanne napinanie osi. Jeżeli napinanie jest silniejsze od odprężania, to oś zestawu będzie się odkształcać skrętnie tak długo aż koła zestawu naruszą przyczepność do toru.

Techniczny przypadek ruchu nie napędzanego zestawu w łuku o małym promieniu może stanowić wymowną ilustrację zjawiska przyczepności oraz sprzężonego z tym pojęcia dynamicznego konturu adhezyjnego, który został zilustrowany rysunkiem 1.10.

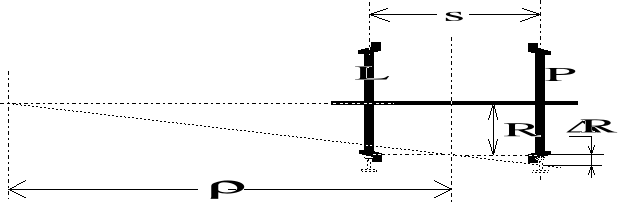
Rysunek 1.12. Ilustracja nieustannego napinania osi w łuku toru o małym promieniu.

Warunek wymuszonego naruszania przyczepności (w procesie ustalonym) przez zestaw toczny w krzywiźnie toru jest następujący:

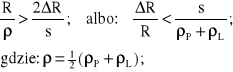
(1.16)

gdzie: s - rozstaw szyn;

- promień krzywizny toru;

W przypadku spełnionego warunku (1.16) napinanie osi jest szybsze niż jej odprężanie.

Uwzględniając wyrażenie (1.15) możemy napisać:

(1.17)

Według aproksymacji - zgodnie z wzorem Cartera - otrzymujemy:

(1.18)

gdzie =(V) - współczynnik przyczepności;

Współczynnik ten jest opisany empirycznym wzorem Andrewsa:

Oczywiście, Fmax = Fmax(V); oznacza graniczną wartość siły przyczepności zgodnie z zależnością: Fmax(V) = Q(V);

gdzie: Q [N] - nacisk koła na szynę.

Moc tracona na "odprężanie" zestawu w łuku wynosi P = FsR/; [Nm] albo

P = FVs/; (1.19)

gdzie V [m/s] jest prędkością ruchu środka zestawu kół wzdłuż toru.

1.10. Elelementarny przykład obliczeniowy.

Rozważmy ruch w łuku zestawu kół zespołu trakcyjnego o następujących wartościach parametrów:

Nacisk koła na szynę Q=5104 [N];

Rozstaw szyn s= 1,5 [m];

Promień okręgów tocznych R=0,5 [m];

Średnica osi pomiędzy kołami zestawu d=0,16 [m];

Moduł sprężystości postaciowej dla stali G=8,0851010 [N/m2];

Prędkość jazdy zestawu w torze V=10[m/s];

Promień łuku = const., potraktujemy jako skokowo zmienny parametr.

Obliczamy kolejno:

Współczynnik przyczepności według Andrewsa:

Współczynnik "c" w uproszczonym wzorze Cartera:

Maksymalna wartość momentu skręcającego w osi zestawu, na granicy przyczepności, przy zadanej prędkości, wynosi:

Sztywność skrętna osi zestawu wynosi:

Maksymalny kąt skręcenia osi zestawu (w opisanych warunkach pracy) wynosi:

Maksymalny (bezwzględny) przyrost promienia trakcyjnego R wynosi:

Droga przejazdu zestawu po prostej, niezbędna dla całkowitego odprężenia maksymalnego skręcenia zestawu, wynosiłaby:

Graniczny promień łuku, na którym jest podtrzymywane maksymalne skręcenie osi [zestawu walcowego] przy zadanej prędkości:

Moc tracona na mikropoślizgi graniczne podczas ruchu zestawu w łuku o promieniu =656[m] wynosi:

Moc tracona na mikropoślizgi graniczne podczas ruchu zestawu w łuku o promieniu =120[m] wynosi:

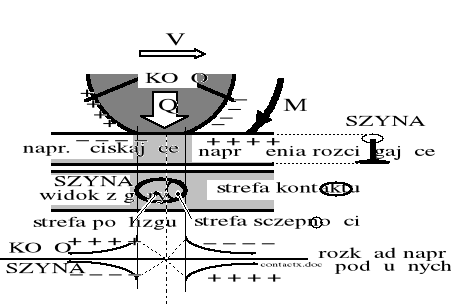
Rysunek 1.13. Charakter rozkładu naprężeń w strefie przyczepności koła i szyny. Rysunek sporządzono wzorując się na ilustracji zamieszczonej w pracy [15].

Podczas ruchu w łuku toru o promieniu mniejszym od granicznego, ślizgający się zestaw napędny może wywiązywać jedynie nieznaczną siłę pociągową, mając pewną nadwyżkę siły pociągowej na szynie wewnętrznej łuku, dzięki opadającej krzywej F(Vśl).

1.11. Podsumowanie rozdziału 1.

1. Uproszczony model mikropoślizgu trakcyjnego, przy znanej wartości współczynników lub , pozwala na bardzo proste i dostatecznie wierne (dla celów modelowania dynamicznego) uwzględnienie wzdłużnych, trakcyjnych skutków złożonych zjawisk kontaktowych.

2. Pojęcie poślizgu opisanego poprzez abstrakcyjne przyrosty promienia koła

R jest łatwe w zastosowaniach obliczeniowych.

3. Model odwzorowuje tylko mikropoślizgi podłużne; poślizgi poprzeczne wymagają oddzielnego potraktowania.

4. Model jest adekwatny do badania dynamiki pojedynczych kół oraz zestawów kolejowych kół napędzanych i nie napędzanych (tocznych).

5. Model z dobrą dokładnością obejmuje przypadki techniczne

6. Model formalnie nie obejmuje granicznego przypadku zablokowania koła przez hamulec kiedy R=; wtedy mamy do czynienia z klasycznym przypadkiem tarcia.

7. Model dotyczy koła "walcowego"; mikropoślizgi poprzeczne, spin (poślizg wiertny) i nabieganie obrzeża na szynę należy uwzględniać przy użyciu oddzielnego modelu.

8. Badanie podłużnej (płaskiej) dynamiki trakcyjnej całego pojazdu i dynamiki układów napędowych powinno być prowadzone łącznie; pasożytnicze obciążenia konturu dynamicznego zestawu obniżają jego użytkową wydajność trakcyjną.

1

20

d)

b)

c)

a)

R_t=R_k⋅sinα

Rysunek 1.2. Ilustracja stycznej współpracy sztywnej kuli lub torusu koła o przekroju kołowym ze sztywną bieżnią rowkową. Linia styku łukowo zakrzywiona. Siły pionowe F_z nie zostały pokazane.

---