8. GEOMETRIA ANALITYCZNA PR
Wierzchołkami trójkąta są punkty
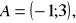
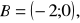
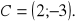
Napisz równanie prostej zawierającej wysokość tego trójkąta poprowadzona z wierzchołka
oraz oblicz pole tego trójkąta. (4 pkt)
Napisz równanie okręgu, którego średnicą jest odcinek prostej
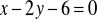
wycięty przez hiperbolę o równaniu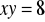
. Wykonaj odpowiedni rysunek. (4 pkt)
Do okręgu o równaniu
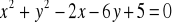
poprowadzono styczne równoległe do prostej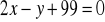
. Wyznacz współrzędne punktów styczności i napisz równanie tych stycznych. (5 pkt)
W trapezie
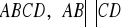
dane są wierzchołki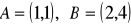
oraz punkt przecięcia przekątnych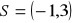
. Pole wynosi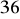
. Oblicz długość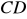
oraz współrzędne pozostałych wierzchołków. (6 pkt)
Znajdź współrzędne wierzchołków trójkąta którego boki zawierają się w prostych o równaniach:
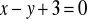
,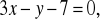
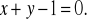
Wykaż że trójkąt jest prostokątny. (4 pkt)
Oblicz pole trójkąta
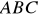
w którym dany jest wierzchołek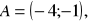
środek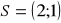
boku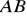
i wektor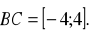
Napisz równanie symetralnej boku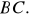
(4 pkt)
Napisz równanie stycznych do okręgu o równaniu

przechodzących przez początek układu współrzędnych. Oblicz pole trójkąta ograniczonego tymi stycznymi i prostą o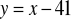
. (4 pkt)
Jaką figurą na płaszczyźnie jest zbiór wierzchołków parabol o równaniach:
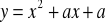
? Napisz równanie tej figury. (3 pkt)Prosta o równaniu

przecina parabolę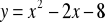
w punktach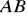
. Oblicz pole i obwód trójkąta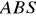
, gdzie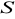
jest wierzchołkiem paraboli. Napisz równanie okręgu opisanego na trójkącie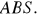
(5 pkt)
Dwa boki równoległoboku zawierają się w prostych o równaniach
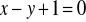
,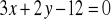
. Punkt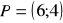
jest punktem przecięcia się przekątnych równoległoboku. Napisz równanie prostych zawierających pozostałe boki. Wyznacz współrzędne wierzchołków równoległoboku i oblicz jego pole. (5 pkt)
Wyznacz współrzędne wierzchołka
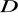
kwadratu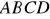
, gdy: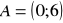
,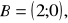
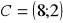
. Napisz równania prostych zawierających przekątne kwadratu. Znajdź równanie okręgu opisanego na tym kwadracie. (4 pkt)Punkty
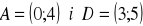
są wierzchołkami trapezu równoramiennego
. Podstawy trapezu są prostopadłe do prostej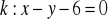
przechodzącej przez punkt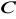
. Wyznacz współrzędne pozostałych wierzchołków trapezu i oblicz jego pole. (6 pkt)
Wyznacz równania stycznych do okręgu równaniu:
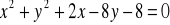
w punktach przecięcia tego okręgu z prostą: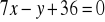
. Oblicz pole trójkąta, którego wierzchołkami są punkty styczności i środek okręgu. (5 pkt)
Punkty
i
są punktami wspólnymi okręgu o równaniu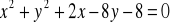
i prostej o równaniu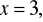
przy czym rzędna punktu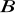
jest większa od rzędnej punktu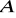
. Znajdź zbiór punktów , których odległość od punktu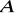
jest dwukrotne większa od odległości od punktu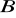
. Jaka to figura? (6 pkt)
Para liczb

jest rozwiązaniem układu równań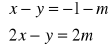
. Dla jakich wartości parametru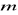
punkt
należy do koła o promieniu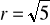
i środku w początku układu współrzędnych? (4 pkt)
W układzie współrzędnych są dane punkty:
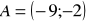
oraz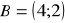
. Wyznacz współrzędne punktu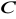
leżącego na osi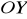
tak że kąt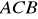
jest kątem prostym. (3 pkt)
Sprawdź, że przekształcenie
płaszczyzny dane wzorem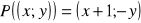
jest izometrią. Wyznacz równanie obrazu okręgu o równaniu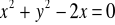
w przekształceniu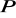
. (3 pkt)
Dla jakich wartości parametru
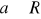
prosta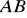
jest prostopadła do prostej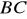
, jeżeli: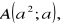
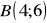
,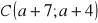
? (4 pkt)
Odcinek
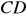
jest obrazem odcinka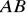
w jednokładności o skali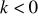
. Wiedząc, że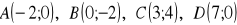
wyznacz: (3 pkt)
równanie prostej przechodzącej przez punkt
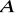
i jego obraz w tej jednokładności,równanie prostej przechodzącej przez punkt
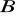
i jego obraz w tej jednokładności,współrzędne środka tej jednokładności.
Punkt

jest jednym z końców odcinka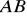
. Punkt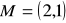
należy do odcinka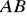
i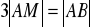
. Oblicz współrzędne punktu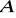
. (3 pkt)
Dane są punkty
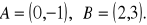
Na prostej o równaniu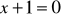
wyznacz punkt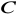
tak, aby trójkąt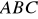
miał najmniejszy obwód. (3 pkt)
Napisz równanie prostych przechodzących przez początek układu współrzędnych i stycznych do okręgu
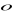
danego równaniem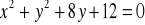
. (3 pkt)
Punkt
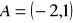
, jest jednym z wierzchołków rombu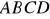
, a punkt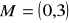
jest środkiem symetrii tego rombu. Pole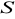
rombu jest równe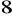
. Oblicz współrzędne pozostałych wierzchołków tego rombu. Narysuj rysunek pomocniczy. (6 pkt)
Punkty
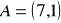
i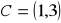
są przeciwległymi wierzchołkami trapezu równoramiennego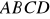
. Prosta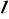
o równaniu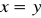
jest osią symetrii tego trapezu. Napisz równanie okręgu opisanego na tym trapezie i oblicz pole trapezu. (5 pkt)
Czworokąt
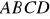
gdzie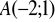
;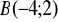
;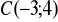
jest trapezem, w którym przekątna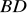
jest dwusieczną kąta przy wierzchołku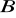
. Wyznacz współrzędne punktu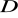
. Znajdź równanie okręgu opisanego na trapezie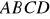
. (5 pkt)
Koło
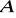
jest ograniczone okręgiem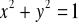
. Koło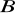
ma środek w punkcie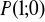
i promień o długości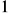
. Oblicz pole zbiorów:
oraz
. (4 pkt)
Z punktu
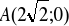
poprowadzono do okręgu o równaniu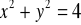
dwie proste, styczne do okręgu w punktach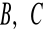
. Znajdź kąt miedzy stycznymi. Znajdź długość odcinka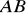
. Znajdź najmniejszą odległość między punktami okręgu i punktem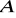
. (4 pkt)
Wyznacz równanie prostej stycznej do okręgu
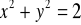
w punkcie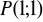
. (3 pkt)
Dany jest okrąg o równaniu
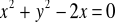
oraz punkt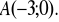
Z punktu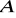
poprowadzono styczne do tego okręgu w punkcie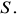
Wyznacz równania tych stycznych i długość odcinka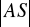
. (5 pkt)Odcinek o końcach
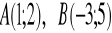
podzielono na trzy równe części. Wyznacz współrzędne punktów podziału. (4 pkt)
Jak względem siebie położone są okręgi o równaniach
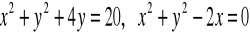
? (3 pkt)
Zaznacz zbiór
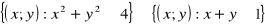
punktów płaszczyzny i napisz równanie jego osi symetrii. (4 pkt)
Zaznacz zbiór
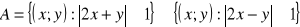
punktów płaszczyzny. Oblicz jego pole i wyznacz równania osi symetrii. (4 pkt)
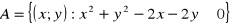
,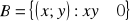
są zbiorami punktów płaszczyzny. Oblicz pole zbioru
. (4 pkt)
Zaznacz zbiór

punktów płaszczyzny i oblicz jego pole. (3 pkt)
Zaznacz zbiór punktów płaszczyzny, których współrzędne spełniają warunek
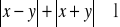
. Czy jest on zawarty w kole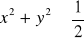
? Wyznacz równanie jego osi symetrii. (4 pkt)
Zaznacz zbiór tych punktów płaszczyzny, których współrzędne spełniają warunek
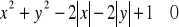
. Znajdź jego środek symetrii. (4 pkt)
Okręgi o równaniach:
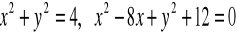
są do siebie styczne w punkcie
i są styczne do prostej o równaniu
w punktach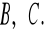
Oblicz pole trójkąta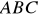
. Jaki to trójkąt? (4 pkt)
Z punktu
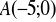
poprowadzono styczne do okręgu o równaniu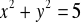
w punktach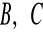
. Wyznacz długość odcinków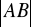
i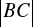
. Oblicz tangens kąta utworzonego przez styczne. (4 pkt)
Określ wzajemne położenie prostej o równaniu
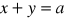
, i okrąg o równaniu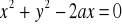
niezależnie od wyboru liczby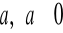
. (3 pkt)
Pary liczb
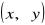
spełniające układ równań: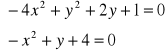
są współrzędnymi wierzchołków czworokąta wypukłego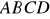
. (2005) (6 pkt)
a) Wyznacz współrzędne punktów: ![]()
.
b) Wykaż, że czworokąt ![]()
jest trapezem równoramiennym.
c) Wyznacz równanie okręgu opisanego na czworokącie ![]()
.
Punkty
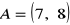
i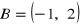
są wierzchołkami trójkąta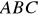
, w którym
. (2006) (6 pkt)
a) Wyznacz współrzędne wierzchołka ![]()
, wiedząc, że leży on na osi ![]()
.
b) Napisz równanie obrazu okręgu opisanego na trójkącie ![]()
w
jednokładności o środku w punkcie ![]()
i skali ![]()
.
Podstawa
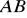
trapezu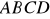
jest zawarta w osi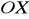
, wierzchołek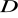
jest punktem przecięcia paraboli o równaniu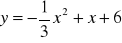
z osią
. Pozostałe wierzchołki trapezu również leżą na tej paraboli. Oblicz pole tego trapezu. (2006) (4 pkt)
Wierzchołki trójkąta równobocznego
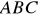
są punktami paraboli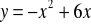
. Punkt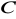
jest jej wierzchołkiem, a bok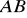
jest równoległy do osi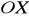
. Sporządź rysunek w układzie współrzędnych i wyznacz współrzędne wierzchołków tego trójkąta. (2007) (6 pkt)
Określ wzajemne położenie prostych o równaniach :
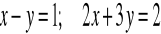
. Oblicz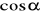
kąta jaki tworzą one ze sobą. (3 pkt)
Dany jest wektor
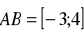
oraz punkt
. Oblicz współrzędne punktu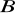
oraz współrzędne i długość wektora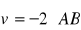
. (3 pkt)
Prostą o równaniu
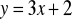
przesunięto o wektor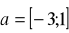
. Napisz równanie otrzymanej prostej. (2 pkt)
Jak względem siebie położone są: prosta zawierająca punkty
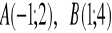
oraz wektor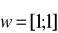
? Uzasadnij odpowiedź. (2 pkt)
Punkty
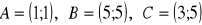
są wierzchołkami trapezu równoramiennego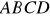
niebędącego równoległobokiem, w którym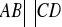
. (CKE) (4 pkt)
Wyznacz równanie osi symetrii tego trapezu.
Oblicz pole tego trapezu.
Wyznacz równanie okręgu o środku

, stycznego do prostej o równaniu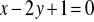
. (CKE) (3 pkt)
Dane są punkty
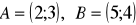
. Na prostej o równaniu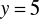
wyznacz punkt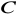
tak, aby łamana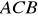
miała jak najmniejszą długość. Odpowiedź uzasadnij. (CKE) (3 pkt)
Uzasadnij, że każdy punkt paraboli o równaniu
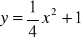
jest równoodległy od osi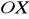
i od punktu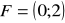
. (2008) (4 pkt)
Wyznacz współrzędne środka jednokładności, w której obrazem okręgu o równaniu
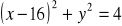
jest okrąg o równaniu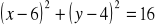
, a skala tej jednokładności jest liczbą ujemną. (2008) (4 pkt)
Prosta
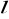
przechodzi przez początek układu współrzędnych. Napisz równanie tej prostej, wiedząc, że jej odległość od punktu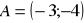
jest równa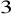
. (2008) (5 pkt)
Jeden z końców odcinka leży na paraboli o równaniu
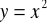
, a drugi na prostej o równaniu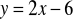
. Wykaż, że długość tego odcinka jest nie mniejsza od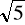
. Sporządź odpowiedni rysunek. (2009) (5 pkt)
Środek okręgu przechodzącego przez punkty
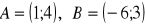
leży na osi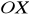
. (2009) (6 pkt)
a) Wyznacz równanie tego okręgu.
b) Wyznacz równanie prostej prostopadłej do prostej ![]()
i oddalonej
od początku układu współrzędnych o ![]()
.
W układzie współrzędnych narysuj okrąg o równaniu
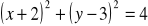
oraz zaznacz punkt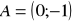
. Prosta o równaniu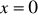
jest jedną ze stycznych do tego okręgu przechodzących przez punkt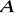
. Wyznacz równanie drugiej stycznej do tego okręgu, przechodzącej przez punkt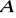
. (2009) (5 pkt)
Obrazem odcinka
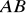
, gdzie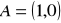
i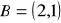
w jednokładności o skali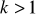
i środku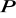
jest odcinek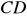
, gdzie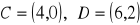
. Zapisz równanie okręgu o środku w punkcie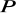
i promieniu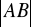
. (2009) (5 pkt)
Punkty rownoodległe od prostej o równaniu
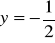
i punktu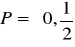
należą do wykresu funkcji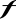
. Znajdź wzór tej funkcji. (2009) (4 pkt)
Dane są zbiory
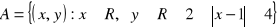
oraz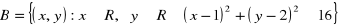
. W układzie współrzędnych zaznacz
i oblicz pole otrzymanej figury. (5 pkt)
Punkt
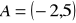
jest jednym z wierzchołków trójkąta równoramiennego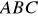
, w którym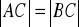
. Pole tego trójkąta jest równe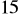
. Bok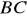
jest zawarty w prostej o równaniu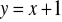
. Oblicz współrzędne wierzchołka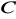
. (2010) (6 pkt)
Punkty
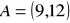
oraz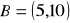
leżą na okręgu, którego środek leży na prostej o równaniu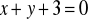
. Wyznacz równanie tego okręgu. (4 pkt)
Rozpatrujemy wszystkie prostokąty o polu równym 6, których dwa sąsiednie boki zawarte są w osiach
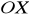
i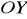
układu współrzędnych. Wyznacz równanie krzywej będącej zbiorem tych wierzchołków rozpatrywanych prostokątów, które nie leżą na żadnej z osi układu współrzędnych. Narysuj tę krzywą. (CKE) (4 pkt)
Oblicz miarę kąta między stycznymi do okręgu
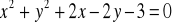
poprowadzonymi przez punkt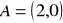
(2011) (4 pkt)
ZADANIA DODATKOWE
W trójkącie
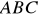
jest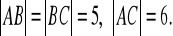
Znajdź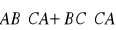
.
Dla jakich wartości parametru
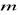
wektory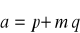
i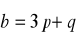
są prostopadłe, jeżeli wiadomo, że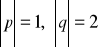
oraz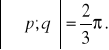
Obliczyć długość wektora
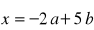
wiedząc, że wektory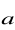
i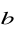
tworzą kąt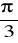
oraz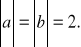
Jak względem siebie położone są wektory
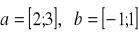
? Znajdź kosinus kąta między nimi. Znajdź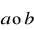
.
Dana jest prosta
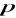
o równaniu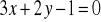
oraz wektor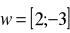
. Określić położenie wektora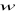
względem prostej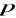
.
Dane są wektory
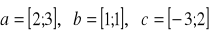
. Czy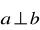
,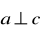
? Znajdź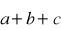
.
Dane są punkty
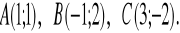
Wyznacz
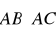
;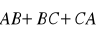
.Czy punkty
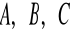
są wierzchołkami trójkąta ?
Punkty
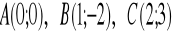
są wierzchołkami trójkąta. Wyznacz:
a) ![]()
;
b) ![]()
;
c) punkt przecinają się środkowych boków trójkąta ![]()
.
Dane są: punkt
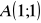
i wektor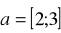
. Czy prosta o równaniu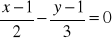
zawiera punkt
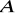
;jest równoległa do wektora
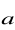
;jest prostopadła do wektora
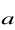
?
Prosta przechodząca przez punkty
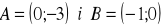
przecina parabolę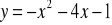
w punktach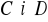
.
Napisz równanie stycznych do paraboli w punktach
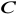
i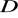
.Wyznacz punkt
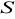
przecięcia się stycznych oraz napisz równanie okręgu o środku w punkcie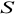
i promieniu równym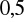
długości odcinka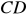
.
© MIROSŁAW JEDLIŃSKI
2
Wyszukiwarka