3.7. Zjawiska termoelektryczne

Do zjawisk termoelektrycznych zalicza się efekty: Peltier'a, Seebeck'a i Thomson'a.

Nazwa zjawiska Peltier'a pochodzi od nazwiska jego odkrywcy, J.C.A. Peltier'a (1785-1845), który w r 1834 zauważył, że temperatura spoin wykonanych z różnych metali zależy od kierunku prądu przepływającego przez te spoiny.

W przypadku dwóch spoin wykonanych z różnych materiałów przewodzących podczas przepływu prądu stałego jedna z nich się nagrzewa zaś druga chłodzi.

Efekt wydzielania ciepła jest niezależny od ciepła Joule'a-Lentz'a i posiada inną naturę.

Zjawiskiem Seebeck'a (T.J. Seebeck, 1770-1831, uczony niemiecki) nazywa się powstawanie siły elektromotorycznej w obwodzie zawierającym dwie spoiny lub złącza wykonane przez połączenie dwóch różnych materiałów przewodzących, jeśli złącza te znajdują się w różnych temperaturach.

Zjawisko Thomson'a polega na wydzielaniu lub pochłanianiu ciepła, dodatkowo do ciepła Joule'a-Lentz'a, przy przepływie prądu stałego wzdłuż próbki z jednorodnego materiału (pół)prze-wodzącego, w warunkach występowania na niej różnicy temperatur. Zjawisko to nie ma znaczenia technicznego

Wymienione zjawiska występują zarówno w metalach jak i w materiałach półprzewodnikowych.

Efekt Peltier'a opisuje współczynnik Peltier'a :

(3.7.1)

gdzie Q_Π jest ilością ciepła wydzielającego się do otoczenia (znak +) lub pochłanianego z otoczenia (znak -) na złączu, jeżeli przepływa przez nie prąd I w czasie t.

Współczynnik Seebeck'a  określony jest zależnością:

(3.7.2)

gdzie dU jes różnicą potencjałów powstającą między złączami, między którymi występuje różnica temperatur dT.

Współczynnik Thomson'a _T zdefiniowany jest zależnością:

(3.7.3)

gdzie dQ_T jest ilością ciepła wydzielającego się (lub pochłanianego) na długości próbki dx, jeżeli przepływa przez nią prąd o wartości I i występuje na niej gradient temperatury (dT/dx).

Wymienione wyżej współczynniki są ze sobą związane za pomocą tzw. relacji Thomson'a:

(3.7.4.a)

(3.7.4.b)

3.7.1. Natura zjawiska Peltier'a

Mechanizm fizyczny prowadzący do wymienionego zjawiska można prześledzić w oparciu o model przedstawiony na Rys. 3.7.1.

Rys.3.7.1. Uproszczony model złącza metal-półprzewodnik.

W przedstawionym modelu przyjęto oznaczenia:

• W_F - poziom Fermi'ego;

• W_C - położenie dna pasma przewodnictwa w półprzewodniku;

• W_K - średnia wartość energii kinetycznej elektronów w paśmie przewodnictwa.

Ponadto założono, że pole elektryczne w półprzewodniku jest bardzo małe (pasma nie są nachylone) oraz równe prace wyjścia z metalu i półprzewodnika - równość poziomów Fermi'ego przed doprowadzeniem do styku.

W warunkach równowagi termodynamicznej poziom Fermi'ego jest jednakowy w obu materiałach.

Jeżeli do złącza jak na Rys.3.7.1. przyłożymy pole elektryczne w zaznaczonym kierunku wówczas elektrony będą przechodziły z pasma przewodnictwa półprzewodnika do metalu, przy czym będą zmuszone w sąsiedztwie styku oddać zgromadzoną energię potencjalną o wartości W.

Energia ta to ciepło Peltier'a wydzielające się w sąsiedztwie złącza przy transporcie przez nie ładunku równego jednemu elektronowi. Można zatem zapisać:

(3.7.5)

Jeżeli pole E skierować przeciwnie, wówczas z metalu do półprzewodnika mogą przejść jedynie elektrony posiadające odpowiednio wysoką energię cieplną-kinetyczną - tzw. gorące elektrony.

Zubożenie obszaru przyległego do złącza w wysokoenergetyczne elektrony prowadzi do obniżenia średniej energii elektronów w paśmie i w konsekwencji do obniżenia temperatury sieci, od której tę energię pobierają dochodząc do równowagi termodynamicznej.

Okolica złącza będzie się zatem ochładzać.

Wartość wymienianej energii na złączu (wydzielanej lub pochłanianej) określa zależność:

(3.7.6)

gdzie W_K jest średnią energią kinetyczną elektronów w paśmie przewodnictwa.

Zakładając, że energia kinetyczna elektronów na dnie pasma przewodnictwa jest równa zeru można ją, dla elektronów w paśmie, określić z zależności:

(3.7.7)

gdzie współczynnik r przyjmuje wartości od 0 do 2 - w zależności od mechanizmu rozpraszania nośników ładunku, k - stała Boltzman'a, T - temperatura.

Z równań (3.7.5), (3.7.6) i (3.7.7) otrzymuje się:

(3.7.8)

Przy wyprowadzeniu wartości współczynnika Peltier'a  nie uwzględniono roli metalu elektrody.

Wynika to z faktu, że efekt Peltier'a jest w przypadku materiałów półprzewodnikowych znacznie wyższy niż w przypadku metali (o rząd wielkości) i jego rolę można zaniedbać.

3.7.2. Natura zjawiska Seebeck'a

Uproszczoną analizę efektu Seebeck'a można przeprowadzić w oparciu o model próbki półprzewodnika, przedstawiony na Rys.3.7.2.

Jeśli próbkę nagrzać nierównomiernie, wówczas na skutek różnicy energii i koncentracji nośników ładunku zacznie się ich ukierunkowany ruch.

Jeżeli końce próbki znajdują się w temperaturach T₁ < T₂ wówczas na końcu próbki o temperaturze T₂ będzie występowała wyższa koncentracja nośników ładunku, jak również będą one posiadały wyższą energię. W efekcie wystąpi ich dyfuzja w kierunku zimniejszego końca (T₁).

Rys. 3.7.2. Zjawisko Seebeck'a w półprzewodnikach z różnymi typami nośników - dyfuzja wynikająca z różnicy koncentracji

W materiałach o stałej koncentracji nośników (metale) ruch nośników w stronę końca o niższej temperaturze wywołuje różnica w ich energiach kinetycznych. Zjawisko ilustruje Rys. 3.7.3.

Rys. 3.7.3. Zjawisko Seebeck'a w materiale o stałej koncentracji nośników.

Na Rys. 3.7.3. wektorami V₁ i V₂ oznaczono prędkości nośników w temperaturach T₁ i T₂,. przyjmując dla T₁>T₂ V₁>V₂., W przypadku różnicy temperatur jak na Rys 3.7.3., pomiędzy końcami próbki wystąpi ukierunkowany ruch nośników w kierunku zadanym przez wektor prędkości V₁.

Przepływ prądu dyfuzji prowadzi do pojawienia się rozkładu potencjału oraz wystąpienia prądu unoszenia.

W warunkach równowagi obie składowe prądu są sobie równe i na zewnątrz obserwujemy tylko różnicę potencjałów między punktami o różnej temperaturze.

Jeżeli nośnikami ładunku są elektrony (półprzewodnik typu „n”) zimniejszy koniec próbki będzie miał w stosunku do cieplejszego potencjał ujemny. Dla półprzewodnika typu „p” - dodatni.

Powyższe podaje prosty sposób określania typu przewodnictwa (elektronowe/dziurowe) w materiałach półprzewodnikowych.

Wartość oraz przebieg w funkcji temperatury współczynnika Seebeck'a  można określić dla materiału półprzewodnikowego o zadanym typie przewodnictwa wiążąc różnicę W_C - W_F z równowagową koncentracją nośników ładunku n₀. W przypadku półprzewodnika typu „n” koncentrację elektronów n₀ określa zależność:

(3.7.9)

Korzystając z zależności (3.7.4.a), (3.7.8) i (3.7.9) można napisać:

(3.7.10)

Podobne rozważania prowadzą dla półprzewodnika typu „p” do zależności:

(3.7.11)

gdzie: N_C, n, N_V, p, są koncentracjami stanów i nośników w paśmie odpowiednio przewodnictwa i walencyjnym.

W przypadku kilku rodzajów nośników lub mechanizmów przewodnictwa wartość współczynnika  określa wzór:

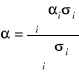
(3.7.12)

gdzie _i jest parcjalną siłą termoelektryczną, określoną nośnikami wnoszącymi do ogólnej konduktywności wkład o wartości σ_i.

Przydatność materiałów do wytwarzania elementów termoelektrycznych określa tzw. dobroć Z, zdefiniowana:

(3.7.13)

gdzie  - współczynnik Seebeck'a [V/K], σ - konduktywność [m]^-1, γ - przewodność cieplna [W/(K m)]. Dielektryki: duże  ale bardzo małe σ (Z=1-2 x 10^-12 [1/K]). Metale: duże σ ale male  i duże γ (Z=1-2 x 10^-5 [1/K]). Dla półprzewodników Z= 1-3 x 10^-3 [1/K].

3.7.3. Natura zjawiska Thomson'a

Zjawisko Thomson'a do chwili obecnej ma znaczenie tylko teoretyczne. Gradient temperatury prowadzi do wystąpienia gradientu koncentracji nośników i odpowiadającemu mu prądowi dyfuzji. Ostatni prowadzi do powstania rozkładu ładunku przestrzennego. Jeżeli pole od ładunku w objętości jest skierowane przeciwnie niż pole zewnętrzne, to ostatnie wykonuje pracę przeciwko polu wewnętrznemu, co prowadzi do wydzielenia dodatkowego ciepła. Jeżeli kierunki obu pól są zgodne, to pole wewnętrzne wspomaga dryft nośników kosztem cieplnej energii sieci, co prowadzi do jej ochłodzenia.

3.7.4. Zastosowanie zjawisk termoelektrycznych

Głównym zastosowaniem efektu Peltiera są tzw pompy cieplne, wykorzystywane tak do nagrzewania jak i do chłodzenia niewielkich obiektów.

Pompy wykonywane są na bazie materiałów półprzewodnikowych, dla których elektrony przechodzące przez złącze zmieniają znacznie energię potencjalną (W_C-W_F).

Rys.3.7.4. Zastosowanie półprzewodników typu „p” i „n” w pompach cieplnych Peltier'a. Kombinacja wielu par styków z półprzewodnikami „p” i „n” pozwala stworzyć technicznie użyteczną pompę ciepła.

Schemat podstawowej struktury pompy przedstawiono na Rys. 3.7.4., zaś pół-

przekrój gotowego elementu pompującego na Rys.3.7.5.

Rys. 3.7.5. Odsłonięta struktura typowego elementu Peltier'a.

Przykładowy element pompujący typu TES1-2725 o wymiarach 30 x 30 mm, o grubości struktury 3.6 mm i o budowie przedstawionej na Rys. 3.7.4 wykazuje następujące własności:

• maksymalny prąd: 2.5 A;

• maksymalne napięcie na strukturze 14.7 V;

• maksymalna różnica temperatur: 67 °C

• maksymalna wydajność cieplna: 26 W

Efekt Seebeck'a najszersze zastosowanie znalazł w pomiarach temperatury za pośrednictwem termopar.

Układ przeciwsobnie (różnicowo) połączonych termopar wytwarza napięcie zależne do różnicy temperatur, w których umieszczono spoiny termopar.

Ponieważ zależność napięcia od różnicy temperatur jest na ogół nieliniowa, podaje się ją w postaci charakterystyk bądź tabelaryzuje. Wymienione charakterystyki są różne w zależności od materiałów stosowanych na spoiny.

Pomimo niewielkiej wydajności źródeł energii elektrycznej, jakim jest termopara, bywa ona wykorzystywana do wytwarzania bądź energii zasilającej współczesne energooszczędne układy elektroniczne, bądź też do zasilania prostych układów wykonawczych, stosowanych w automatyce. Przykładem może być przedstawiony na Rys. 3.7.6. układ zabezpieczenia zaniku gazu,

Rys.3.7.6. Układ zabezpieczenia zaniku ciśnienia gazu w piecu c.o. wykorzystujący termoparę.

wykorzystywany w typowych piecach centralnego ogrzewania opalanych gazem.

W przedstawionym przypadku prąd stały, wytwarzany przez termoparę nagrzewaną płomieniem palnika pilotującego, zasila elektromagnes utrzymujący zawór odcinający gaz w położeniu „otwarty”. W przypadku zaniku gazu palnik pilotujący gaśnie, siła elektromotoryczna spada do zera, zawór się zamyka i nie możliwości wypływu gazu przy ponownym wzroście jego ciśnienia.

LITERATURA

1. Oreskin P. T., Fizika poluprovodnikov i dielektrikov. Izd. Vyssaja Skola, Moskva

1977.

2. Tauc J., Zjawiska fotelektryczne i termoelektryczne w półprzewodnikach, PWN,

Warszawa 1966.

3. Szalimowa K.W. Fizyka półprzewodników, PWN, Warszawa, 1974.

4. Smith R.A., Półprzewodniki, PWN, Warszawa 1966.

---