Wydatek objętościowy

Wydatkiem objętościowym strugi będziemy nazywali iloczyn prędkości przez pole przekroju w płaszczyźnie prostopadłej do wektora prędkości.

DQ=VdS_n=VndS=VdScosα

Gdzie n oznacza wersor powierzchni S. „Zwrot” powierzchni jest określony zwrotem normalnej; przyjmuje się, że zwrot jest dodatni, jeżeli jest zgodny ze zwrotem wektora prędkości (wydatek musi być dodatni).

Wydatek strumienia nazywany jest również strumieniem wektora. Wyrażenie

dQ/dS=Wn=lim_Δs-0ΔQ/ΔS Nazywa się natężeniem pola wektorowego. Jest ono w danym punkcie pola równe rzutowi wektora na na normalną do elementu powierzchni dS.

RÓWNANIE RUCHU EULERA

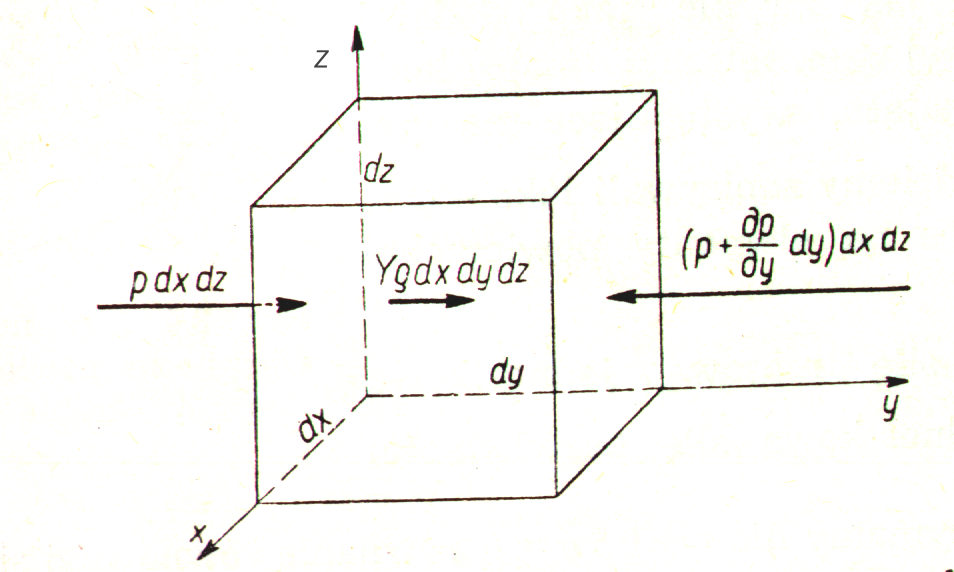
Rozpatrujemy element płynu o wymiarach dx, dy, dz. Na element ten działają tylko siły masowe oraz siły powierzchniowe. W przypadku płynu doskonałego (nielepkiego i nieściśliwego) siłami powierzchniowymi mogą być tylko siły normalne ściskające.

Rys. W2/2. Siły działające na element płynu

Równanie ciągłości dla ruchu ustalonego płynu ściśliwego

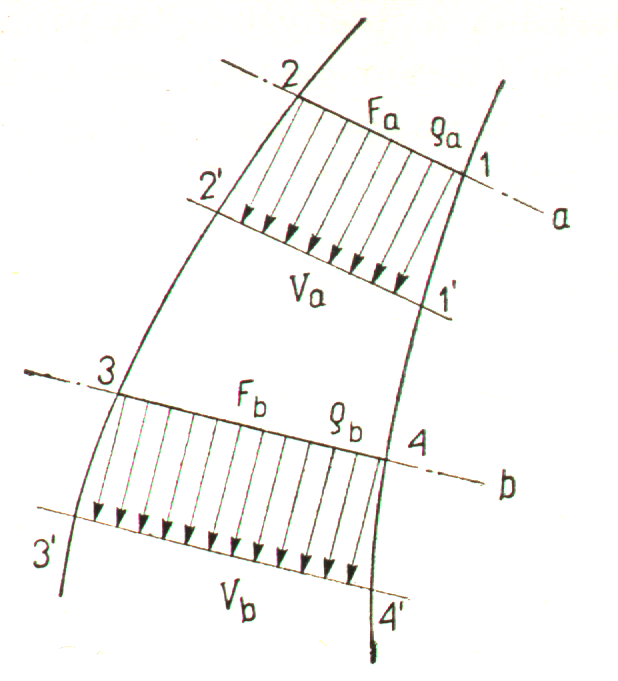
Rozpatrujemy dwa przekroje strugi płynu ściśliwego. Zakładamy, że przekroje te stanowią powierzchnie przez które może przenikać materia; powierzchnie boczne niech będą ściankami nieprzepuszczalnymi (np. rzeczywiste ścianki rury).

Przez przekrój a wpływa do przestrzeni kontrolnej masa ρ_aV_aF_a. W tym samym czasie przez przekrój b wypływa masa ρ_bV_bF_b. Z warunku zachowania masy w objętości kontrolnej wynika, że ρ_aV_aF_a= ρ_bV_bF_b.

Równanie to jest słuszne dla jednowymiarowego przepływu ustalonego czynnika ściśliwego. Z równania tego wynika bardzo ważny wniosek dotyczący przepływów w przewodach o zmiennym przekroju: zmiana średnicy przewodu musi powodować zmiany gęstości płynu oraz jego prędkości. W przypadku płynów nieściśliwych zmiana przekroju przewodu powoduje jedynie zmianę prędkości przepływu.

---