Agnieszka Chojnacka kl 1c/B1
Elementy szczególnej teorii względności
1. Pojęcie układu odniesienia, ruchy w różnych układach odniesienia ( V<C )
Odpowiedni układ odniesienia jest niezbędny do opisu ruchu ciał materialnych, czyli należy wybrać jeden lub kilka ciał, które przyjmiemy za nie zmieniające swej pozycji. Ruchem ciał nazywamy zmiany ich położenia względem obranego uprzednio układu odniesienia.
Układ odniesienia, w którym ciało nie poddane działaniu sił pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym nazywamy układem inercjalnym. Każdy układ poruszający się względem układu inercjalnego ruchem jednostajnym jest też układem inercjalnym.
Prędkość światła dla obserwatora w różnych układach odniesienia, co się dzieje z czasem
Prędkość światła jest niezależna od układu odniesienia.
Ogólnie obowiązuje klasyczne prawo dodawania prędkości.
np.
jeżeli ciało1 porusza się z prędkością 8 m/s, a goni go ciało2 z prędkością 12 m/s, to prędkość ciała1 względem ciała2 wynosi 4 m/s.
W przypadku gdyby ciało1 porusza się naprzeciw drugiego, to ich względna prędkość byłaby sumą prędkości względem podłoża i wynosiłaby 20 m/s. Z tą prędkością zbliżają się do siebie.
Dodawanie prędkości:
c = c - v (1)
c = c + v (2)
W kinematyce nierelatywistycznej obowiązuje:
x' = x - vt t = t' (3)
Natomiast w przypadku kinematyki relatywistycznej wprowadzono współczynnik ၧ
x' =ၧ(x - vt) x = ၧ'(x' + vt') (4)
Skoro nie istnieje wyróżniony układ współrzędnych inercjalnych, to ၧ' = ၧ (4a)
Szukając transformacji czasu
x = ၧ(x' + vt') პ x - ၧ x' = ၧ vt' ->
ale x' = ၧ(x - vt) czyli
(5)
(6)
(7)
(8)
c2ၧ2 - v2 ၧ2 = c2 z tego warunku wynika, że
(9)
Czyli:
(10)
Znając ၧ przekształcamy wzór i otrzymujemy
(11)
Transformuje się czas! To w fizyce klasycznej nie występuje.
Tak otrzymane transformacje relatywistyczne, zwane transformacjami Lorentza, które w przypadku ruchu układu w dodatnim kierunku osi x, mają następującą postać:
x' = ၧ(x - vt)
y' = y
z' = z
ၧ Ⴓ 1, bo v Ⴃ c
Prawu dodawania prędkości nie podlega jednak światło. Potwierdza to doświadczenie Michelsona - Morleya.
Próbowano sprawdzić prędkość rozchodzenia się światła w układzie związanym z Ziemią. Dzięki temu, iż nasza planeta okrąża Słońce z prędkością 30 m/s, to efekt zmiany prędkości światła względem planety powinien dać się zauważyć, gdy:
-światło porusza się zgodnie z ruchem Ziemi
-światło porusza się przeciwnie do ruchu Ziemi
prędkość światła
prędkość Ziemi
prędkość światła
Prędkość względna powinna być sumą prędkości Ziemi i prędkości światła podczas zbliżaniu się Ziemi i światła, za to w sytuacji gdy Ziemia „goni” światło prędkość względna powinna być równa różnicy tych prędkości. Zaistniał niestety pewien problem do rozstrzygnięcia - może górne warstwy powietrza, w których teoretycznie miało rozchodzić się światło poruszają się w którąś stronę? Dałoby się wykryć ewentualny ruch eteru jako zmiany prędkości światła dla różnych kierunków ruchu Ziemi.
Dzięki specjalnie skonstruowanemu urządzeniu zwanym interferometrem Michelsona można było dokonać słynnego doświadczenia wykonanym w 1881 roku. Rozstrzygnął one problem ruchu naszej planety względem górnych warstw powietrza. W sześć lat później doświadczenie zostało powtórzone przez Michelsona wspólnie z Morleyem.. Jego wynik był jednak całkowicie zaskakujący - bez względu na kierunek ruchu Ziemi, porę dnia i roku, kierunek ustawienia ramion interferometru - odczyty wykazywały na to samo - że prędkość światła względem Ziemi ma zawsze tę samą wartość.
Można dlatego powiedzieć, iż wykrywana prędkość światła względem Ziemi jest niezależna od tego, czy jest skierowana zgodnie, czy przeciwnie względem prędkości naszej planety.
Doświadczanie było wielokrotnie powtarzane w różnych warunkach i czy to poruszając się naprzeciw światłu, czy zgodnie z kierunkiem jego prędkości, to zawsze prędkość względna wynosiła dokładnie tyle samo: c = 299792458 m/s - czyli w przybliżeniu 300 tys. km/s. Wykazało to, iż koncepcja eteru jest pozbawiona podstaw fizycznych - eteru nie ma, a światło nie rozchodzi się "w czymś", tylko "względem układu odniesienia".
Dla ciała poruszającego się z szybkością v' w układzie U', którego prędkość w układzie U ma ten sam kierunek i zwrot, co v, szybkość w układzie U jest równa:
v=
Gdy prędkości v i u są zwrócone przeciwnie i u>v', to stosujemy wzór
v=
Wydłużenie czasu.
Po podstawieniu do równania które uległo transformacji danych dla zdarzeń obserwowanych z poruszającego się układu odniesienia, okazuje się że te same zjawiska są widziane tak, jak by zachodziły wolniej. Jest to tzw. wydłużenie czasu w układach poruszających się. Np. jeśli będziemy obserwować zegarek umieszczony na satelicie poruszającej się z dużą prędkością, to stwierdzimy, że zegarek ten spóźnia się względem identycznego, znajdującego się na Ziemi. Nie wynika to z wady zegarka, lecz widziany w obiekcie poruszającym się czas płynie wolniej, czyli dla obserwatora w środku poruszającego się układu, wszystko jest tak, jak było, a dla obserwatora z zewnątrz - zachodzące tam zdarzenia zachodzą wolniej.
Zegar spoczywa w początku układu S. Mierzy odstęp czasu ၄t między zjawiskami, które zaszły w tym samym punkcie układu S' np. x', (t1', t2').
->
Wskazania zegara w układzie S są większe od wskazań w układzie S'.
- Umieszczenie zegarów atomowych na pokładzie samolotu lecącego dookoła świata i na Ziemi. Zauważono wówczas, że zegary, które znajdowały się na pokładzie samolotu, były nieco "młodsze". Pokazywały inny czas niż zegary znajdujące się na Ziemi. Co prawda o milionowe czy nawet miliardowe części sekundy, ale były młodsze...
- Umieszczenie zegarów atomowych w okolicach biegunów i równika. Wiadomo, że Ziemia kręci się dookoła własnej osi, a osią obrotu ziemi są bieguny. Więc prędkość punktu znajdującego się na biegunie jest zerowa, natomiast prędkość punktu znajdującego się na równiku wynosi ok. 1670 km/h, więc zegary znajdujące się na równiku nieco chodzą wolniej.
Skrócenie długości
Odległość widziana w obiekcie poruszającym się będzie skrócona. Zachodzi to tylko w kierunku ruchu.
Podobnym zjawiskiem do wydłużenia czasu jest skrócenie długości.
Można przez to rozumieć zjawisko polegające na tym, iż ciało, które porusza się blisko nas wydaje się być krótsze, niż jest w rzeczywistości. Efekt ten zachodzi jednak tylko w kierunku ruchu - gdyby owe ciało było ustawione prostopadle do prędkości, to zarówno w układzie w którym spoczywa, jak i w tym w którym się porusza - cały czas będzie miała dokładnie taką samą długość. Wynika z tego np. że przelatująca kula zamienia się dla obserwatora widzącego ją w ruchu w elipsoidę.
Pręt spoczywa w układzie S', jego długość spoczynkowa
l0 = x2` - x1' = ၄x'
Obserwator O w układzie S mierzy jednocześnie położenie obu końców pręta.
x2` - x1' = ၧ(x2 - vt) - ၧ(x1 - vt) = ၧ(x2 - x1)
၄x' = ၧ ၄x
ၧ Ⴓ 1 პ ၄x < ၄x'
Długość L mierzona przez obserwatora O w układzie S jest mniejsza niż zmierzona w układzie S'.
Światło - sposób przekazywania informacji
Najlepszym przykładem na zastosowanie światła przy przekazywaniu informacji są światłowody, czyli włókna szklane (ewentualnie tworzywa sztuczne - nie stosowane w telekomunikacji), w których odbywa się propagacja światła, czyli ruch zaburzenia w medium dzięki "całkowitemu" (niewielka ilość przenika przez płaszcz) wewnętrznemu odbiciu.
Światłowody są wykorzystywane jako elementy urządzeń optoelektronicznych, składniki optycznych układów zintegrowanych lub do transmisji sygnałów na duże odległości, jak również do celów oświetleniowych.
Wykorzystują one zjawisko całkowitego wewnętrznego odbicia, które zachodzi dla fal (najbardziej znane dla światła) występujące na granicy ośrodków o różnych współczynnikach załamania. Polega ono na tym, że światło padające na granicę od strony ośrodka o wyższym współczynniku załamania pod kątem większym niż kąt graniczny, nie przechodzi do drugiego ośrodka, lecz ulega całkowitemu odbiciu.
Prawa obowiązujące przy dodawaniu prędkości bliskiej C
Układ S' porusza się z prędkością v wzdłuż osi x. Punkt materialny porusza się z prędkością u w układzie S, a z prędkością u' w układzie S'.
Obliczamy składowe prędkości w układzie S'.
Składowe uy i uz zależą od składowej równoległej do osi x.
Bibliografia:
D. Halliday, Fizyka, wyd 9
J,. Blinowski, W. Zielicz, Fizyka i astronomia, cz. 1, WsiP, Warszawa 2002
http://www.wiem.onet.pl/
1
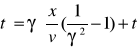
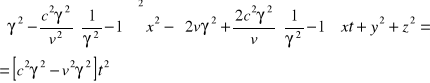
12 m/s
8 m/s
8 m/s
12 m/s
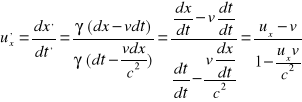
Wyszukiwarka
Podobne podstrony:
9463
9463
9463
9463
więcej podobnych podstron