Magdalena Plęs nr43
Zadania projektowe z Inżynierii bioprocesowej
Projekt I
Zadanie 1.
W izolowanym cieplnie cylindrycznym zbiorniku o średnicy D należy ogrzać ciecz o objętości V od temperatury T1 do T2 . Gęstość cieczy wynosi ၲ, a jej ciepło właściwe c. Do ogrzewania ma być wykorzystana gorąca woda o początkowej temperaturze t1 przepływająca wężownicą zainstalowana w zbiorniku i wykonaną z rury stalowej o średnicy dw/dz. Średnica zwoju wężownicy stanowi połowę średnicy zbiornika D. Doświadczalnie stwierdzono, że współczynnik wnikania ciepła od ścianki wężownicy do cieczy wynosi ၡ2. Mieszadło zapewnia idealne wymieszanie cieczy w zbiorniku, zaś pojemność cieplna układu „zbiornik + mieszadło + wężownica” stanowi 20% pojemności cieczy ogrzewanej.
Należy określić konieczną długość wężownicy L, jeśli czas zagrzewania nie może być dłuższy niż ၴ, zaś prędkość wody w wężownicy wyniesie u.
Dane:
V=9,7 m3
T1=288K
T2=318K
t1=340K
ၲ=1030![]()
c=3,95![]()
dw=40mm
dz=44mm
ၴ=140min
u=0,9![]()
D=1,9m
ၡ2=1050![]()
Dane zmienione ze względu na brak możliwości rozwiązania zadania:
ၴ=200min
1.Obliczam średnice zwoju wężownicy:
Dw=D/2 Dw=1,9/2=0,95m
2.Ponieważ temperatura wody w wężownicy jest różna, wprowadzam
temperaturę średnią, którą obliczam z zależności:
tśr=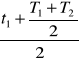
tśr=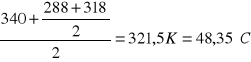
3. Dane fizykochemiczne dla wody, potrzebne do obliczeń, otrzymuję poprzez interpolację poniższych wartości w przedziale 30-60![]()
co 10![]()
T/ |
ၲ/(kg/m3) |
C/(kJ/kg*K) |
ၬ/(W/m*K) |
ၭ/10-4(Pa*s) |
30 |
995,7 |
4,174 |
0,618 |
8,01 |
40 |
992,2 |
4,174 |
0,634 |
6,53 |
50 |
988,1 |
4,174 |
0,648 |
5,49 |
60 |
983,2 |
4,179 |
0,659 |
4,70 |
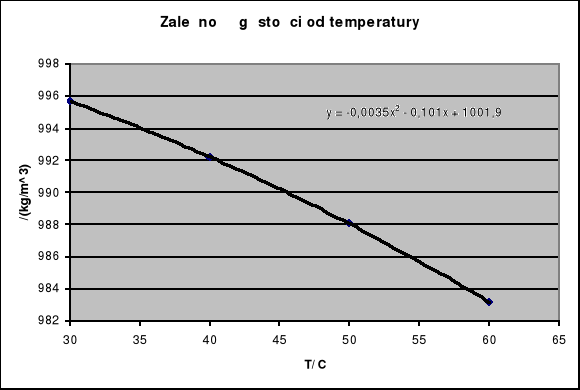
Równanie krzywej:
ၲ=-0,0035T2-0,101T+1001,9 zatem gęstość wody dla temperatury 48,35![]()
wynosi:
ၲ=-0,0035*48,352-0,101*48,35+1001,9=988,8 kg/m3
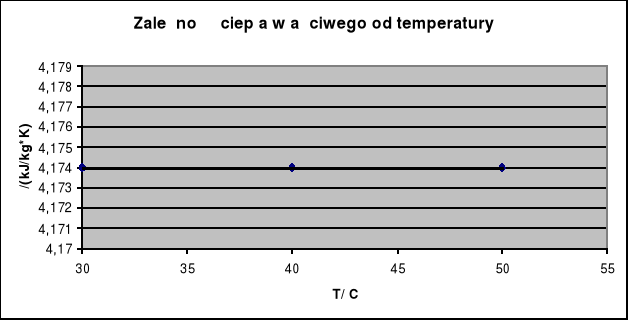
Ciepło właściwe wody dla temperatury 48,35![]()
wynosi 4,174 kJ/kg*K
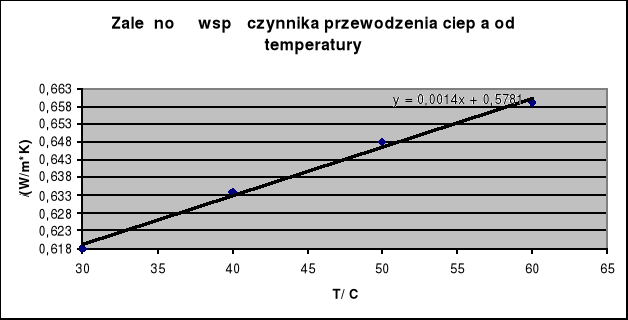
Równanie krzywej:
ၬ=0,0014T+0,5781
Współczynnik przewodzenia ciepła dla wody w temperaturze 48,35![]()
wynosi:
ၬ=0,0014*48,35+0,5781=0,646W/m*K
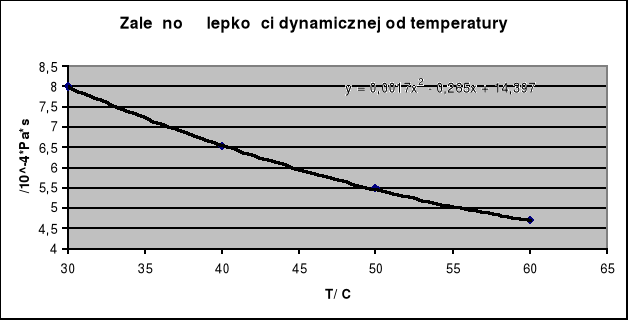
Równanie ma postać:
ၭ=0,0017T2-0,265T+14,375
Lepkość dynamiczna wody w temperaturze 48,35![]()
wynosi:
ၭ=0,0017*48,352-0,265*48,35+14,397=5,56*10-4Pa*s
4. W celu obliczenie współczynnika wnikania dla wody w temperaturze
48,35![]()
obliczam:
-liczbę Prandtla
Pr=![]()
; liczba ta jest jedną z liczb podobieństwa, wyraża stosunek momentu dyfuzyjnego do dyfuzji na drodze termicznej:
Pr=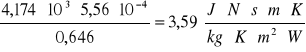
![]()
wielkość bezwymiarowa
-liczbę Reynoldsa
Re=![]()
; liczba ta jest jedną z liczb podobieństwa, wyraża stosunek sił bezwładności do sił lepkości (przedstawia charakter przepływu):
Re=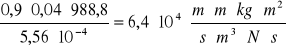
![]()
wielkość bezwymiarowa
-liczbe Nuselta
Nu=![]()
; liczba ta jest jedną z liczb prawdopodobieństwa, wyraża
stosunek szybkości ruchu na drodze wnikania do szybkości ruchu na drodze przewodzenia:
Nu=0,023*(6,4*104)0,8*3,590,4=268,35
Współczynnik wnikania ciepła(dla rury prostej) dla wody w temperaturze 48,35:
![]()
![]()
![]()
Ruch wody grzewczej odbywa się w wężownicy dlatego konieczne jest wprowadzenie poprawki na współczynnik wnikania ciepła:
ၡ1=ၥ1*ၡw
ၥ1=1+3,54![]()
ၡ1=4,334*103*1,149=4,979*103
5.Obliczam grubość ścianki wężownicy:
ၤ=dz-dw=0,044-0,04=0,004m
6.Wielkości wykorzystywane w pózniejszych obliczeniach:
-różnica zastępcza temperatur: ၄tz=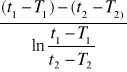
-współczynnik przewodzenia ciepła dla stali: ၬs=58![]()
-średnia logarytmiczna(charakterystyczna dla powierzchni cylindrycznych) powierzchni zewnętrznej i wewnętrznej wężownicy(wprowadzona ze względu na nieznajomość długości wężownicy):
Fm=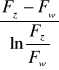
, gdzie
Fz=ၰ*L*dz -powierzchnia zewnętrzna wężownicy
Fw=ၰ*L*dw -powierzchnia zewnętrzna wężownicy
-współczynnik przenikania ciepła kz:
![]()
=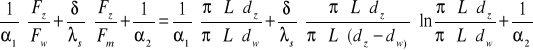
![]()
kz=860![]()
7. Ponieważ temperatury obu płynów(wody i płynu w reaktorze) zmieniają się wraz ze zmianą długości wężownicy, zatem muszę obliczyć średnią temperaturę zastępczą(၄tz), której wzór podałam wyżej. Wyprowadzę jej wartość wykonując kilka przekształceń poniższego wzoru:
dQ=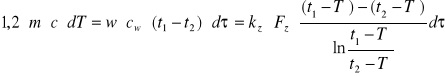
, gdzie:
-pierwszy człon równania oznacza ciepło pobrane przez zbiornik w czasie dၴ, temperatura w zbiorniku zmieniła się wówczas o dT;
-drugi człon równania oznacza ciepło oddane przez wodę znajdującą się w wężownicy cieczy w zbiorniku w różniczkowym czasie dၴ ;
-trzeci człon równania oznacza ciepło, które przeszło przez ściankę wężownicy w różniczkowym czasie dၴ;
Oznaczenia wielkości znajdujących się w równaniu:
m- masa cieczy
![]()
w-natężenie przepływu wody w wężownicy
![]()
c- ciepło właściwe cieczy w reaktorze
cw - ciepło właściwe wody
8.Obliczam masę cieczy i natężenie przepływu wody:
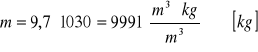
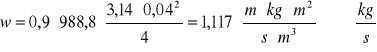
9. Obliczam czas minimalny by sprawdzić czy mój podany czas nie jest za krótki na przebieg procesu:
-porównując:
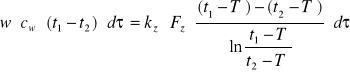
a następnie przekształcając, otrzymuję:
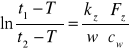
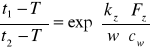
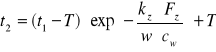
-podstawiając otrzymane wyrażenia na t2 do wyrażenia na ciepło oddane przez wodę w wężownicy w różniczkowym czasie ![]()
otrzymuję:
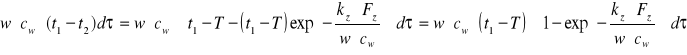
-następnie porównuję wyrażenie na ciepło pobrane przez ciecz w zbiorniku oraz przekształcone równanie na ciepło oddane przez wodę płynącą w wężownicy w różniczkowym czasie ![]()
:
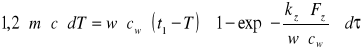
, po przekształceniu
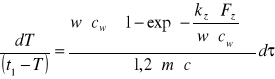
-całkując otrzymane wyrażenie w granicach: ![]()
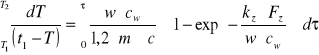
![]()
![]()
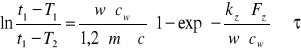
-pomijam wyrażenie 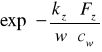
i otrzymuję wyrażenie na czas minimalny:
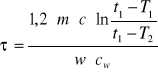
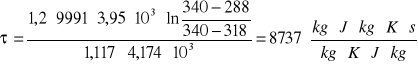
![]()
Obliczony czas minimalny jest większy niż czas podany w zadaniu(ၴ=140min) więc by proces przebiegał prawidłowo wydłużam czas do ၴ=200min.
10. Obliczam powierzchnię zewnętrzną wężownicy, przekształcając odpowiednio powyższe równanie:
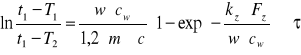
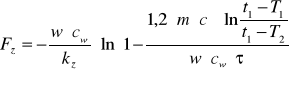

![]()
12. Obliczam długość wężownicy
L=![]()
Zadanie2
W przeponowym wymienniku ciepła należy schłodzić strumień pewnej cieczy od temperatury T1 do temperatury T2. Natężenie przepływu strumienia cieczy wynosi w1, zaś jej ciepło właściwe - c. Ciecz jest chłodzona strumieniem wody o natężeniu w2 i temperaturze początkowej t0. Sumaryczny współczynnik przenikania ciepła wynosi K.
Obliczyć konieczna powierzchnie wymiany ciepła przy zastosowaniu:
przeciwprądu
współprądu
prądu skrzyżowanego.
Dane:
T1=364![]()
T2=324![]()
t0=288![]()
w1=0,134![]()
w2=1,14![]()
c=4,64![]()
K=0,182![]()
Przy wykonywaniu obliczeń będę korzystać z bilansu natężeń przepływu.
a)Powierzchnia wymiany ciepła przy zastosowaniu przeciwprądu:
1.Obliczam ciepło cieczy chłodzącej:
![]()
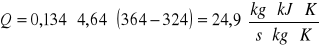
![]()
2.Obliczam t1 korzystając z zależności:
![]()
, gdzie cw oznacza ciepło właściwe wody w temperaturze t0=288K=14,85ႰC, którego wartość otrzymam poprzez interpolację poniższych wartości w przedziale 0-40ႰC ![]()
T/ႰC |
Cw/(kJ/kg*K) |
0 |
4,212 |
10 |
4,191 |
20 |
4,183 |
30 |
4,174 |
40 |
4,175 |
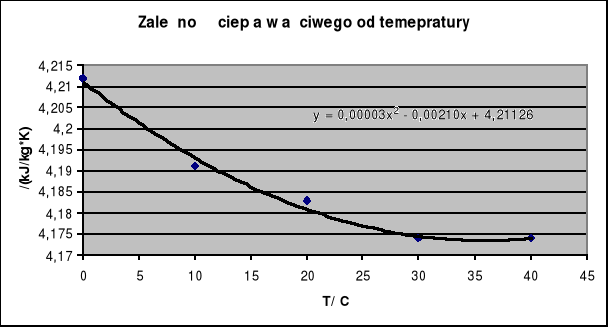
Równanie ma postać:
cw=0,00003*T2-0,0021*T+4,21126
Ciepło właściwe wody w temperaturze 14,85ႰC wynosi:
Cw=0,00003*14,852-0,0021*14,85+4,21126=4,187![]()
![]()
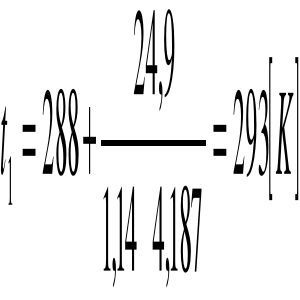
3.Obliczam zastępczą różnicę temperatur dla układu pracującego w przeciwprądzie:
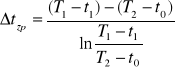
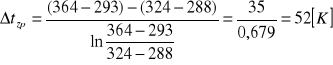
4. Obliczam powierzchnię wymiany ciepła:
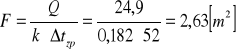
b) Powierzchnia wymiany ciepła przy zastosowaniu współprądu:
1.Ciepło cieczy chłodzącej:
![]()
![]()
2.Tepmeratura t1:
![]()
3.Obliczam zastępczą różnicę temperatur dla układu pracującego we współpradzie:
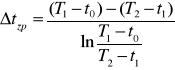
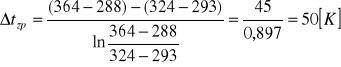
4. Obliczam powierzchnię wymiany ciepła:
![]()
c)Powierzchnia wymiany ciepła przy zastosowaniu prądu skrzyżowanego:
1.Ciepło cieczy chłodzącej:
![]()
![]()
2.Tepmeratura t1:
![]()
3. Aby policzyć zastępczą różnicę temperatur korzystam ze wzoru ![]()
(Y- czynnik poprawkowy) należy wyznaczyć Y.
Wiedząc, że Y = f(X,Z) ,![]()
, ![]()
odnajduję wartość Y na wykresie.
Ponieważ Z=8 , X=0,066 zatem Y=1.
![]()
4.![]()
Zadanie3
W temperaturze t ![]()
w aparacie bełkotkowym przebiega proces napowietrzania płynu fermentacyjnego. Początkowa wysokość cieczy w naczyniu, bez napowietrzania, wynosiła h![]()
. Na dnie umieszczona jest bełkotka mająca n otworów o średnicy d ![]()
. Przepływ gazu wynosi W ![]()
. Należy obliczyć: wielkość pęcherzyków, ich prędkość, powierzchnię międzyfazową oraz porowatość warstwy i jej wysokość, jeżeli średnica aparatu jest równa ![]()
. W obliczeniach przyjąć, że własności cieczy zbliżone są do własności wody.
Dane:
t=40![]()
h=2,8![]()
n=280![]()
d=1,5![]()
W=9![]()
=2,5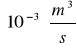
![]()
ρc(40°C)=992,2![]()
ρg=1,128![]()
μc(40°C)=6,53![]()
σ=696*10-4![]()
g=9,81![]()
1. Obliczam przepływ gazu na jeden otwór:
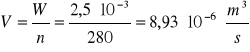
2. Sprawdzam czy mam doczynienia z ruchem laminarnym czy burzliwym.
W tym celu zakładam, ze ruch jest laminarny, obliczam liczbę Reynoldsa i sprawdzam czy jest ona mniejsza lub równa 9 czy też nie:
-obliczam wartość krytyczną przepływu gazu przez jeden otwór:
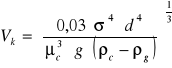
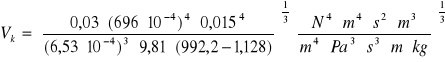
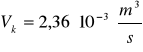
ponieważ Vk>V zatem jest to ruch swobodny
-obliczam średnicę pęcherzyków:
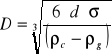
![]()
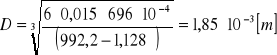
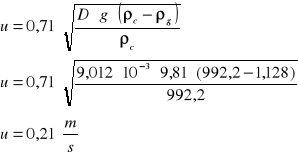
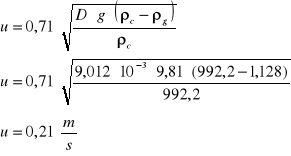
-obliczam prędkość pęcherzyków:
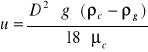
![]()
-obliczam liczbę Reynoldsa:
Re=![]()
![]()
Zatem ruch jest burzliwy.
-obliczam wartość krytyczną przepływu gazu przez jeden otwór:
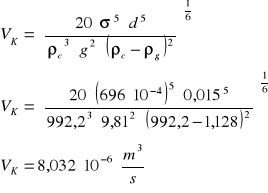
ponieważ V>Vk zatem ruch jest łańcuchowy
-obliczam średnicę pęcherzyków:
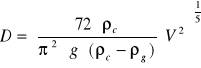
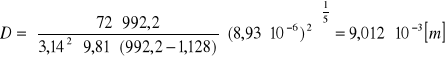
-obliczam prędkość pęcherzyków:
3. Obliczam porowatość warstwy:
![]()
![]()
![]()
6,15![]()
![]()
![]()
4. Obliczam wysokość warstwy:
![]()
![]()
5. Obliczam powierzchnię miedzyfazową, przypadającą na jeden otwór bełkotki i jednostkę wysokości słupa cieczy:
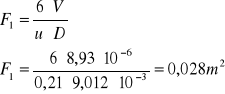
Zadanie 4
Należy obliczyć:
zapotrzebowanie na moc dla mieszadła łapowego o długości łopaty L
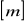
,
wysokości h![]()
, w cylindrycznym zbiorniku o średnicy D![]()
,
zapełnionym do wysokości H![]()
roztworem o właściwościach
zbliżonych do własności wody (roztwór wodny). Mieszadło ma
wykonywać n obrotów na minutę.
jak się zmieni zapotrzebowanie na moc dla tego mieszadła, jeżeli w układzie zostanie zastosowane napowietrzanie z szybkością względną Qg
,jak zmieni się poziom cieczy w zbiorniku w wyniku zatrzymania gazu w układzie
ile wyniesie objętościowy współczynnik przenikania tlenu Kga dla tego układu, oraz jaki będzie strumień absorbowanego tlenu, jeżeli stężenie O2 w cieczy jest o połowę mniejsze niż w stanie nasycenia?
Dane:
T=55![]()
![]()
L=70![]()
h=11,5![]()
D=225![]()
H=405![]()
Qg=0,00800 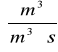
![]()
![]()
Zmieniam dane ze względu na brak możliwości rozwiązania zadania z przydzielonymi wartościami. Dane zmienione:
L= 85![]()
![]()
h=13![]()
1.Obliczam moc dla mieszadła łopatowego:
-obliczam c (stała zależna od geometrii układu):
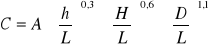
przyjmuję, że A=1
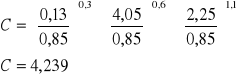
-obliczam liczbę Reynoldsa:
![]()
![]()
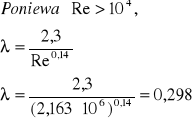
-obliczam moc mieszadła:
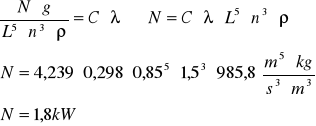
2.Obliczam moc mieszadła podczas napowietrzania:
Kiedy wprowadzimy napowietrzanie z szybkością względną Qg, zmniejszy się zapotrzebowanie na moc mieszadła. Stosunek mocy potrzebnej przy napowietrzaniu do mocy bez napowietrzania jest 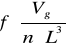
. Stosunek mocy odczytałam z wykresu.
Ng - moc mieszadła gdy układ jest napowietrzany
Vg - natężenie przepływu powietrza doprowadzanego do całego
zbiornika
![]()
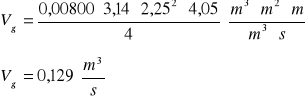
![]()
Z wykresu Ohyamy:
Ng=0,3N
Ng=![]()
3. Obliczam poziom cieczy w zbiorniku:
Aby wyznaczyć wysokość cieczy w zbiorniku po zatrzymaniu gazu, trzeba wyznaczyć współczynnik zatrzymania 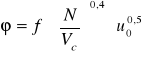
. Współczynnik ten odczytałam z wykresu.
u0-prędkość pozorna gazu w zbiorniku
![]()
![]()
Vc-objętość cieczy w zbiorniku
![]()
![]()
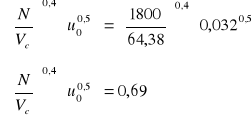
ϕ=0,1%=0,001
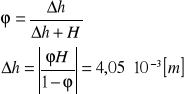
4. Obliczam objętościowy współczynnik przenikania ![]()
dla układu oraz strumień absorbowanego tlenu, jeżeli stężenie O2 w cieczy jest o połowę mniejszy niż w stanie nasycenia.
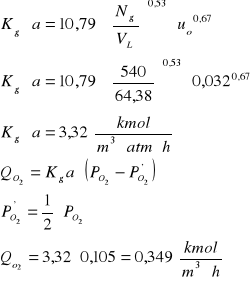
![]()
![]()
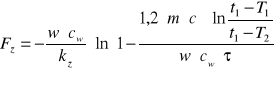
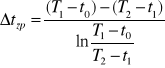
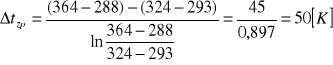
![]()
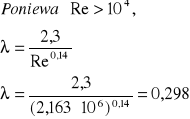
![]()
![]()
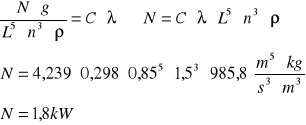
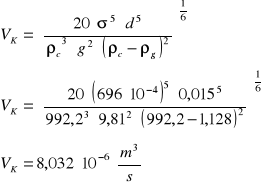
Wyszukiwarka