2. Wybrane zagadnienia statyki pŁynÓw

2.1. Ciśnienie statyczne

Ciśnieniem statycznym (ciśnieniem) nazywamy wielkość fizyczną cha-rakteryzującą działanie siły normalnej na dowolnie zorientowaną powierzchnię znajdującą się wewnątrz płynu, będącego w stanie spoczynku względem pewnego układu odniesienia, i na ścianę naczynia, w którym płyn się znajduje (jest to moduł naprężenia normalnego ściskającego). Ciśnienie w dowolnym punkcie wyznaczamy jako granicę

(2.1)

gdzie
jest siłą parcia otaczającego płynu działającą prostopadle na element po-wierzchni

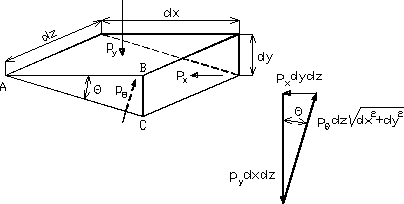
Rys. 2.1

Wykażemy, że ciśnienie w zadanym punkcie płynu nie zależy od kierunku powierzchni (kierunku normalnej do powierzchni). W tym celu rozważmy pryzmatyczny element płynu przedstawiony na rys. 2.1. Na ścianki AB, BC i AC działają siły powierzchniowe. Płyn pozostaje w spoczynku, więc siły powierzchniowe są reprezentowane jedynie składowymi - pochodzącymi od ciśnienia. Ponieważ rozważany element jest mały, możemy pominąć siły grawitacyjne jako znacznie mniejsze od sił ciśnieniowych i znikające w granicy, gdy średnica elementu dąży do zera (siły grawitacyjne są proporcjonalne do objętości elementu, natomiast siły pochodzące od ciśnienia są proporcjonalne do jego powierzchni).

Z warunku równowagi elementu przedstawionego na rys. 2.1 uzyskujemy zależności:

z których wynika, że

(2.2)

Ponieważ kąt θ może przyjmować dowolne wartości - wnioskujemy, że ciśnienie w danym punkcie płynu rzeczywistego, pozostającego w spoczynku, nie zależy od kierunku działania.

2.2. Podstawowe równania równowagi p*ynu

Będziemy badali równowagę płynu, który pozostaje w spoczynku lub porusza się ruchem jednostajnym względem przyjętego układu odniesienia. W tych warunkach nie występuje ruch względny cząstek płynu, a więc siły styczne równają się zeru.

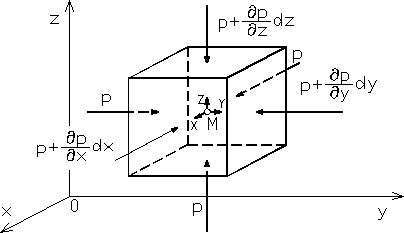
Rys. 2.2

Rozważymy równowagę elementu płynu w kształcie prostopadłościanu o krawędziach
równoległych do odpowiednich osi współrzędnych układu pro-stokątnego x, y, z (rys. 2.2). Na ten element działają siły powierzchniowe normalne (siły ciśnieniowe) oraz siły masowe, określone przez pole jednostkowych sił masowych

(2.3)

Mnożąc rzuty jednostkowej siły masowej X, Y, Z przez masę elementu otrzymamy odpowiednie składowe siły masowej, działającej na elementarny prostopadłościan

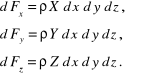
(2.4)

Z warunku równowagi płynu wynika, że suma rzutów sił, działających na element, na dowolnie wybrany kierunek jest równa zeru. Rzutując wymienione siły na kierunek osi x

oraz pisząc analogiczne równanie dla kierunków y i z otrzymamy układ równań różniczkowych

(2.5)

czyli

(2.6)

W najprostszym przypadku, gdy na płyn nie działają siły masowe, tzn. gdy

równanie (2.6) upraszcza się do postaci

(2.7)

Wynik ten jest matematycznym wyrazem prawa Pascala, zgodnie z którym ciśnienie jest stałe w całej masie płynu, jeśli na płyn nie działają siły masowe.

Mnożąc równania (2.5) odpowiednio przez
i dodając je stronami, otrzymamy

(2.8)

Prawa strona tego równania przedstawia różniczkę zupełną ciśnienia
ma-my więc

(2.9)

Sformułujemy obecnie warunki, jakim musi czynić zadość pole sił masowych jednostkowych na to, by znajdujący się w tym polu płyn mógł być w równowadze. Dalsze rozważania ograniczymy do płynów barotropowych , których gęstość jest funkcją wyłącznie ciśnienia

(2.10)

co oznacza, że powierzchnie stałego ciśnienia i powierzchnie stałej gęstości pokrywają się. Płyny, których gęstość zależy nie tylko od ciśnienia nazywane są płynami baroklinowymi .

Dla płynów barotropowych można wprowadzić tzw. funkcję ciśnienia

(2.11)

w związku z czym

(2.12)

Równania równowagi (2.6) przybierają wtedy postać

(2.13)

pole sił masowych jednostkowych
musi być zatem potencjalne; warunek równowagi dla płynów barotropowych jest więc następujący

(2.14)

Płyn barotropowy, a więc również ciecz, może znajdować się w równowadze tylko w potencjalnym polu sił masowych jednostkowych.

Funkcja jest to potencjał sił masowych jednostkowych. Powierzchnie równego potencjału

(2.15)

będziemy nazywać powierzchniami ekwipotencjalnymi .

Składowe siły
(2.4) są pochodnymi potencjału:

zatem równanie (2.9) możemy zapisać w postaci

(2.16)

z której wynika, że między ciśnieniem a potencjałem jednostkowych sił masowych zachodzi zależność liniowa

(2.17)

gdzie C jest stałą całkowania.

Z równania (2.16) wynika także, że powierzchnia ekwipotencjalna jest zarazem powierzchnią jednakowego ciśnienia oraz, że wektor jednostkowych sił masowych jest ortogonalny do powierzchni ekwipotencjalnej w każdym punkcie leżącym na tej powierzchni.

2.3. R*wnowaga cieczy w jednorodnym polu grawitacyjnym

Przypadek równowagi cieczy znajdującej się pod działaniem siły ciężkości, jako jedynej siły masowej w jednorodnym polu grawitacyjnym, jest przypadkiem bardzo ważnym dla praktyki.

Ciecz znajduje się w nieruchomym naczyniu związanym z prostokątnym układem współrzędnych, w sposób pokazany na rys. 2.3. Skladowe jednostkowej siły masowej w dowolnym punkcie wynoszą:

X = 0, Y = 0, Z = g. (2.18)

Podstawiając te wartości do równania (2.9) otrzymujemy różniczkowe równanie rozkładu ciśnienia w obszarze cieczy

(2.19)

i następnie równanie algebraiczne

(2.20)

w którym iloczyn
nazywany jest ciśnieniem hydrostatycznym .

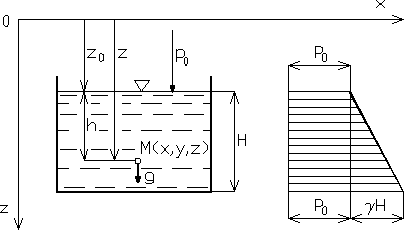
Rys. 2.3

Na powierzchni swobodnej
ciśnienie wynosi
co zezwala na wyznaczenie stałej C

ciśnienie w dowolnym punkcie M wyraża się zatem wzorem

(2.21)

lub też wzorem

(2.22)

gdzie
jest głębokością punktu M.

Jeżeli na swobodnej powierzchni panuje ciśnienie atmosferyczne, wówczas równanie (2.22) przyjmuje postać tzw. wzoru manometrycznego

(2.23)

Powierzchnie jednakowego ciśnienia wyznaczamy ze wzoru (2.19) dla
Są one więc płaszczyznami poziomymi z = const, prostopadłymi do kierunku działania siły ciężkości.

Występujące w równaniu (2.23) ciśnienie p nazywamy ciśnieniem bezwzględnym . Różnicę ciśnienia bezwzględnego i ciśnienia atmosferycznego
nazywamy nadciśnieniem , gdy różnica ta jest dodatnia; podciśnieniem - gdy jest ujemna.

2.4. Parcie cieczy na powierzchnie p*askie

Parciem hydrostatycznym nazywamy siłę powierzchniową, jaką wywiera ciecz będąca w stanie spoczynku na powierzchnię dowolnie zorientowaną w przestrzeni. Jest ona skierowana normalnie do rozpatrywanej płaszczyzny.

Rozważmy parcie cieczy na dowolną powierzchnię σ, znajdującą się na płaskiej ścianie, nachylonej pod kątem α do powierzchni swobodnej (rys. 2.4).

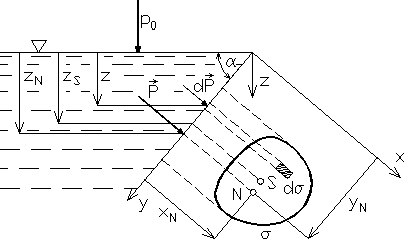
Rys. 2.4

Obieramy ukośny układ współrzędnych w taki sposób, że oś x leży na krawędzi przecięcia się ściany płaskiej z powierzchnią swobodną, oś y prostopadle do osi x w płaszczyźnie ściany oraz oś z pionowo w dół. Obracając ścianę płaską dookoła osi y wykonamy kład rozważanej powierzchni σ na płaszczyznę rysunku.

Zgodnie ze wzorem (2.22) elementarne parcie
działające na element powierzchni
o współrzędnych jego środka x, y, z wynosi

(2.24)

Wypadkowa tych sił, czyli napór cieczy na płaską powierzchnię σ jest zatem równa

(2.25)

gdzie
jest zagłębieniem środka geometrycznego
pola σ pod zwierciadłem cieczy.

Z powyższego wzoru wynika tzw. paradoks hydrostatyczny Pascala , odnoszący się do parcia na poziome dno zbiornika: parcie na poziome dno zbiornika zależy tylko od pola powierzchni dna i od odległości od zwierciadła cieczy, a nie zależy od objętości cieczy zawartej w zbiorniku.

Oznaczmy przez N punkt o współrzędnych
- nazywany środkiem parcia - w którym przyłożona jest siła parcia (2.25). Przyjmując, że ciśnienie na zewnątrz ściany jest równe
czyli rozpatrując parcie netto

(2.26)

z równania momentów względem osi x mamy

(2.27)

Po uwzględnieniu zależności:

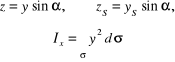
oraz wykorzystaniu twierdzenia Steinera, wyrażającego moment bezwładności przez moment bezwładności pola σ względem osi przechodzącej przez środek ciężkości S i równoległej do osi x

otrzymujemy

(2.28)

Środek parcia na ścianę pochyłą lub pionową leży więc zawsze poniżej środka ciężkości, gdyż

W podobny sposób obliczamy współrzędną środka parcia N, pisząc równanie momentów względem osi y

z którego wyznaczamy

(2.29)

2.5. Parcie cieczy na powierzchnie zakrzywione

Rozważmy prosty przypadek powierzchni cylindrycznej AB, której tworzące są prostopadłe do płaszczyzny
(rys. 2.5a). Oś x obieramy wzdłuż powierzchni swobodnej cieczy, a oś z pionowo w dół.

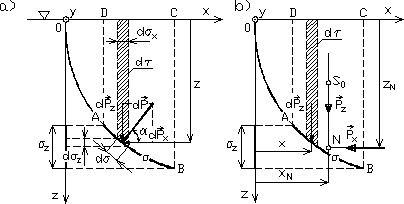
Rys. 2.5

Na powierzchni σ obieramy element
znajdujący się na głębokości z pod zwierciadłem cieczy. Parcie elementarne, normalne do tej powierzchni będzie równe

którego rzuty na kierunki osi współrzędnych x i z wyrażają się wzorami:

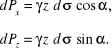
Oznaczmy przez
i
rzuty powierzchni elementu
na płaszczyznę poziomą i płaszczyznę pionową. Po uwzględnieniu zależności:

otrzymamy wyrażenia:

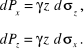
Ich całki po całej powierzchni σ określają składowe: poziomą i pionową parcia cieczy:

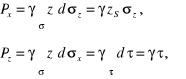
(2.30)

w których z_S jest głębokością środka ciężkości S rzutu pionowego powierzchni
- momentem statycznym powierzchni względem zwierciadła cieczy, a 
przedstawia objętość słupa cieczy znajdującej się nad elementem

Składowa pozioma parcia na powierzchnię zakrzywioną równa jest więc par-ciu na rzut tej powierzchni na płaszczyznę pionową, zaś składowa pionowa rów-na się ciężarowi cieczy znajdującej się w obszarze ABCD, ograniczonym od dołu rozpatrywaną powierzchnią.

Współrzędną środka parcia N (rys. 2.5b) obliczamy ze wzoru (2.28)

(2.31)

Natomiast współrzędną  kierunku działania składowej pionowej parcia obliczamy z równania momentów względem osi y

z którego, po uwzględnieniu zależności
oraz
, uzyskamy

(2.32)

Ze wzoru tego wynika, że parcie pionowe przechodzi przez środek geometryczny obszaru cieczy ABCD.

W zależności od kształtu powierzchni zakrzywionej rozróżniamy dwa rodzaje parcia pionowego:

- dodatnie (skierowane w dół), gdy ciecz wypełnia obszar nad powierzchnią zakrzywioną,

- ujemne (skierowane do góry), gdy obszar ten nie jest wypełniony cieczą.

2.6. Prawo Archimedesa i r*wnowaga cia* zanurzonych

Wyznaczymy siłę wywieraną przez ciecz na ciało stałe całkowicie w niej zanurzone bądź też pływające na swobodnej powierzchni cieczy (rys. 2.6).

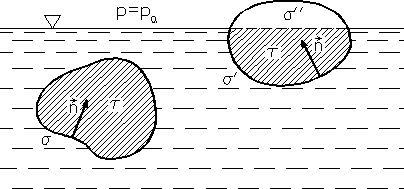
Rys. 2.6

Wypadkowa parć elementarnych wyraża się całką

(2.33)

obliczoną dla całej powierzchni zamkniętej σ - ograniczającej ciało stałe, przy czym
jest normalną zewnętrzną względem ciała.

Z twierdzenia Gaussa-Ostrogradskiego (14.33) mamy

(2.34)

gdzie τ jest obszarem przestrzennym ograniczonym powierzchnią σ; znak minus wynika z faktu przyjęcia normalnej wewnętrznej za dodatnią. Na mocy wzorów (2.13) i (2.18) jest

stąd

(2.35)

gdzie
jest ciężarem wypartego płynu.

W przypadku ciała pływającego ciężar wypartego powietrza możemy pominąć i przyjąć, że

, (2.36)

gdzie
jest ciężarem wypartej cieczy; możemy więc rozważać powierzchnię σ - składającą się z powierzchni zwilżonej i płaskiego odcinka
stanowiącego przekrój ciała zwierciadłem cieczy.

Uzyskany wynik jest treścią znanego prawa Archimedesa, zgodnie z którym wypadkowa parcia cieczy na ciało zanurzone w niej jest wektorem przeciwnym do ciężaru cieczy wypartej przez ciało.

W zagadnieniach pływania ciał parcie nazywane jest wyporem i jest oznaczane literą
Z rozważań przedstawionych w rozdziale 2.5 wynika, że linia działania siły wyporu
przechodzi przez środek ciężkości zanurzonej objętości ciała, traktowanej jako bryła jednorodna.

Warunek stateczności pływania ciała całkowicie zanurzonego jest warunkiem typu jakościowego i może być sformułowany następująco: ciało całkowicie zanurzone pływa statecznie, gdy jego środek wyporu SW znajduje się powyżej środka ciężkości SC tzn. punktu przyłożenia ciężaru
(rys. 2.7a). W tym przypadku po wychyleniu ciała o niewielki kąt α powstaje moment sił
i
który przywróci ciało do pierwotnego stanu równowagi, a środki ciężkości i wyporu znajdą się znowu na tej samej osi pionowej.

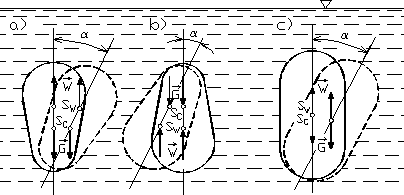
Rys. 2.7

Jeżeli środek ciężkości leży powyżej środka wyporu (rys. 2.7b), wówczas siła ciężkości i wypór utworzą moment, który zwiększy początkowe wychylenie określone kątem α - jest to więc stan równowagi chwiejnej ciała pływającego. Jeśli środek ciężkości pokrywa się ze środkiem wyporu (rys. 2.7c), to siły
i
są w równowadze - ciało po wychyleniu nie zmieni więc swego położenia, czyli znajduje się w stanie równowagi obojętnej.

2.7. R*wnowaga cia* p*ywających

Warunki równowagi ciał pływających na powierzchni cieczy są zupełnie odmienne od warunków równowagi ciał całkowicie zanurzonych, które pływają statecznie tylko w przypadku, gdy środek ciężkości leży poniżej środka wyporu. Ciało pływające na powierzchni cieczy może być również w stanie równowagi trwałej wtedy, gdy środek ciężkości leży nad środkiem wyporu. Jest to związane z faktem zmiany kształtu zanurzonej objętości ciała przy jego wychyleniu i przesuwaniu się środka wyporu SW .

Zagadnienie stateczności dla przypadku gdy środek ciężkości znajduje się powyżej środka wyporu jest szczególnie istotne w praktyce budowy statków i łodzi. Załóżmy zatem, że rozpatrujemy ciało o budowie symetrycznej (rys. 2.8a). Przy wychyleniu ciała o elementarnie mały kąt dookoła osi x - prostopadłej do rysunku (rys. 2.8b), siła ciężkości
i środek ciężkości SC nie zmieniają swego położenia względem ciała. Siła wyporu
nie zmienia swojego modułu , co wynika z warunku równowagi sił w kierunku pionowym, zmienia się natomiast jej linia działania, przechodząca przez przesunięty środek wyporu .

Siła
jest równoważna ciężarowi cieczy zawartej w objętości reprezentowanej przez przekrój A-B-C-D, a siła
przez przekrój A'-B'-C-D. Siły te różnią się tylko wyporami reprezentowanymi przez kliny AOA' oraz BOB'. Oznaczając je odpowiednio przez
i
mamy

(2.37)

Z faktu równości wyporów W i wynika równość wyporów
i
; siły
i
tworzą zatem parę sił.

Wyznaczając moment M siły
względem punktu otrzymujemy

(2.38)

gdzie l jest odległością między siłami
i
,
, a d - odległością między siłami
i

Wartość momentu wyznaczymy teraz za pomocą wielkości geometrycznych ciała pływającego. Przekrój otrzymany z przecięcia statku płaszczyzną lustra cieczy

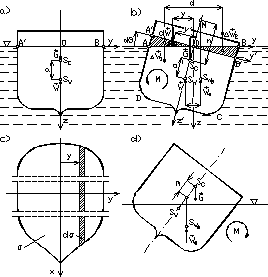
Rys. 2.8

nazywamy płaszczyzną pływania ; pole tej płaszczyzny niech wynosi σ (rys. 2.8c). W celu obliczenia tego momentu podzielimy objętość klinów na elementarne słupki o podstawach
w płaszczyźnie pływania i o wysokościach równych
Elementarny wypór wynosi
a elementarny moment wywołany wyporem tego słupka względem osi x jest równy:
Stąd mamy

(2.39)

36