Laboratorium z Fizyki

Sprawozdanie z ćwiczenia nr 16

Temat: ”Pomiar przyspieszenia ziemskiego przy pomocy wahadła rewersyjnego”

Wykonał:

Paweł Waskian

I Elektronika

Grupa laboratoryjna nr 3

1. Cel ćwiczenia

Celem doświadczenia jest wyznaczenie przyspieszenia ziemskiego za pomocą wahadła rewersyjnego.

2. Część teoretyczna

Ruch drgający może wykonywać każde ciało sztywne, zawieszone tak, aby mogło poruszać się wokół stałej osi O , która nie przechodzi przez jego środek masy S (rys. 1) . Ciało takie nazywamy wahadłem fizycznym .

Ruch wahadła fizycznego podlega drugiej zasadzie dynamiki dla ruchu obrotowego wokół stałej osi .

M.- Moment siły powodujący ruch względem

osi przechodzącej przez punkt zawieszenia

I-moment bezwładności względem tej osi - przyspieszenie kątowe

Siłą działającą na wahadło jest siła ciężkości G zaczepiona w środku masy S . Stąd na podstawie rysunku mamy:

Wartość liczbowa wektora momentu obrotowego M wynosi więc

m - masa

- kąt nachylenia wahadła

Znak minus pochodzi stąd , że moment obrotowy M. jest skierowany przeciwnie niż wektor reprezentujący wychylenie .

Drugą zasadę dynamiki dla ruchu obrotowego wokół stałej osi możemy też zapisać w postaci skalarnej

Dla małych kątów wychylenia wahadła , wobec tego

, a ponieważ , więc

Po podstawieniu otrzymujemy

Jest to równanie różniczkowe ruchu harmonicznego dla wahadła fizycznego , przy czym wielkością , która drga jest kąt wychylenia . Ponieważ droga środka masy , więc ruch środka masy jest także ruchem harmonicznym , podobnie jak ruch dowolnego punktu wahadła fizycznego.

Moment siły dla ( w mierze łukowej ) nazywamy momentem kierującym i oznaczamy przez D , gdzie

Równanie różniczkowe ruchu harmonicznego wahadła fizycznego możemy zatem napisać w postaci

Ponieważ , to na okres drgań wahadła fizycznego przy niewielkich wychyleniach otrzymujemy wyrażenie:

Zależność okresu drgań wahadła fizycznego od położenia punktu zawieszenia.

Zgodnie z twierdzeniem Steinera moment bezwładności wahadła względem osi przechodzącej przez punkt zawieszenia wyraża się wzorem

, gdzie

I₀- moment bezwładności względem osi równoległej do osi zawieszenia przechodzącej przez środek ciężkości

h - odległość obu osi ( odległość środka ciężkości od punktu zawieszenia )

Moment bezwładności względem środka masy ma postać

, gdzie

r_b - ramię bezwładności

Zatem

Stąd okres drgań wahadła fizycznego wynosi

Ze wzoru tego wynika , że dla h0 T, tzn. gdy odległość punktu zawieszenia od środka masy wahadła maleje , to okres jego drgań rośnie. Dla malejącego h okres T , a w miarę wzrost h okres maleje i osiąga minimum dla h = r_b , wtedy

, a dla hr_b okres T znowu rośnie.

Dla danego punktu zawieszenia można podać trzy jeszcze inne punkty zawieszenia dla których wahadło ma ten sam okres drgań . Rozpatrzymy punkty zawieszenia dla obu punktów znajdujące się po obu stronach środka masy wahadła w odległości h i h₁ od niego.

Wzory na okresy drgań dla wahadła zawieszonego w tych punktach będą się przedstawiały następująco:

,

Po obustronnym podniesieniu do kwadratu i odjęciu stronami otrzymujemy

Stąd widać , że okres drgań wahadła zawieszonego w punktach a i c odległych od środka masy o h i h₁ , jest równy okresowi drgań wahadła matematycznego o długości l = h + h₁

Punkt c nazywa się środkiem drgań dla punktu zawieszenia a . Porównując wzory

= otrzymujemy wzór

, z którego możemy wyznaczyć odległość środka drgań od środka masy wahadła ,jeżeli znamy odległość h punktu zawieszenia od środka masy.

Wahadło zawieszone w punkcie a ma ten sam okres drgań co wahadło zawieszone w środku drgań c , przy czym odległość tych punktów ( h + h₁ ) jest równa długości wahadła matematycznego, które ma ten sam okres drgań co dane wahadło fizyczne . Tę długość nazywamy długością zredukowaną wahadła fizycznego.

Rozważania te można zastosować do tzw. wahadła rewersyjnego , które zbudowane jest z pręta mogącego się wahać względem dwóch stałych osi przechodzących przez punkty A i B ( pryzmaty ostrzami skierowane do siebie ) odległe o l . na pręcie zamocowane są dwa ciężarki , które możemy swobodnie przesuwać ; jeden między punktami A i B ; drugi powyżej punktu A . ciężarki przesuwa się tak długo , aż okresy drgań przy zawieszeniu wahadła w punktach A i B będą równe . wtedy l jest długością zredukowaną wahadła . Ponieważ długość l i okres drgań T można wyznaczyć z dużą dokładnością , więc wahadło rewersyjne służy do dokładnych pomiarów przyspieszenia ziemskiego korzystając ze wzoru na okres wahadła matematycznego

3.Część praktyczna

a) Tabela pomiarów

Lp	lz	t1	T1	t2	T2	Tśr
	[m]	[s]	[s]	[s]	[s]	[s]
1	15	12,350	1,2350	12,380	1,2380
2	25	12,176	1,2176	12,199	1,2199
3 4	36 40	12,036 11,868	1,2036 1,1868	12,062 11,890	1,2062 1,1890	1,2031
5	46	11,685	1,1685	11,633	1,1633

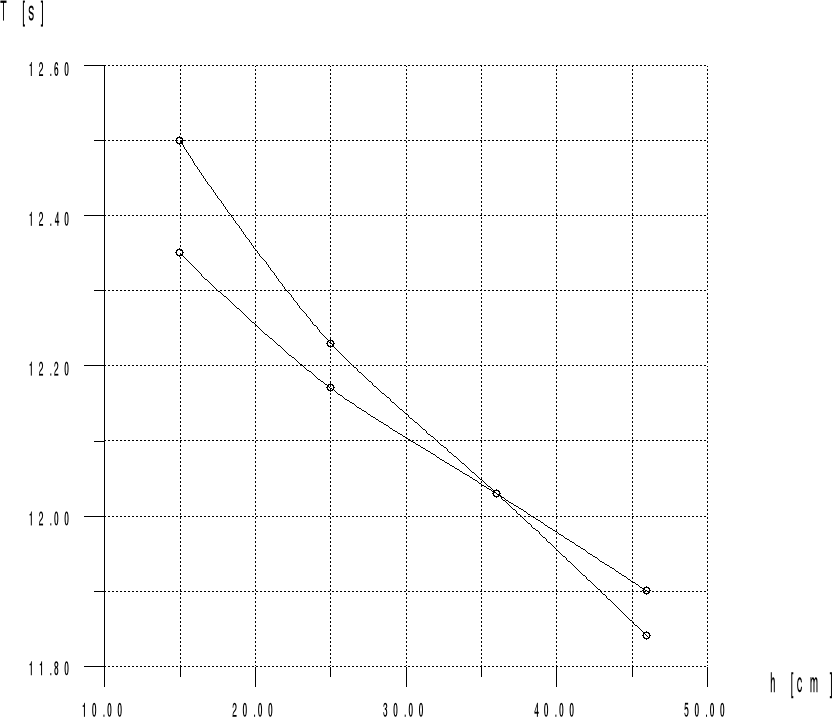
Na podstawie powyższej tabeli został sporządzony wykres, z którego łatwo odczytać zbliżoną wartość długości zredukowanej wahadła .

Lp	n	T	lz	lz śr	lz
		[s]	[m]	[m]	[m.]
1	10	0,03389	0,38		0,02
2	10	0,01592	0,37		0,01
3	10	0,00183	0,36	0,36	0,00
4	10	0,01570	0,35		0,01
5	10	0,03650	0,34		0,02

Metoda liczenia błędów wykonana wg przedziałów ufności

dla

Błąd względny liczymy metodą logarytmiczną

Błąd względny wynosi:

Przyśpieszenie ziemskie wyznaczamy ze wzoru:

Błąd bezwzględny :

Ostatecznie otrzymujemy :

Wnioski :

Ćwiczenie to polegało na wyznaczeniu przyspieszenia ziemskiego za pomocą wahadła rewersyjnego. Głównym celem było znalezienie długości zredukowanej, czyli odległości między dwoma punktami zawieszenia , dla których okresy drgań wahadła były jednakowe. W tym celu stopniowo przesuwaliśmy odważnik na wahadle mierząc okresy drgań na dla obu punktów zawieszenia. Jak wiemy z założeń teoretycznych wahadło matematyczne o długości równej długości zredukowanej ma, także ten sam okres drgań. Wyznaczając doświadczalnie owy okres łatwo już wyliczyć przyspieszenie ziemskie ze wzoru na okres drgań wahadła matematycznego. W ćwiczeniu zaobserwowaliśmy również zależność pomiędzy odległością ciężarka od punktu zawieszenia, która była odwrotnie proporcjonalna do okresu drgań.

Powstały błąd pomiaru może wynikać z niezbyt dobrej stabilności układu pomiarowego oraz braku wypoziomowania. Wyznaczony wynik przyspieszenia ziemskiego jest bardzo bliski rzeczywistemu przyspieszeniu.

---