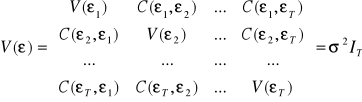II. Funkcja produkcji o stałej elastyczności substytucji (CES lub SMAC):
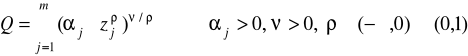
lub 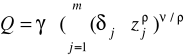
gdzie 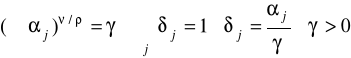
dla ρ→1 CES odpowiada doskonałej substytucyjności (wykres - prosta)
dla ρ→0 CES odpowiada funkcji Cobb-Douglasa (wykres hiperboliczny)
dla ρ→-∞ CES odpowiada technologii Leontieffa (doskonała komplementarność - wykres L)
Produkcyjność krańcowa i-tego czynnika: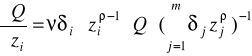
Elastyczność względem i-tego czynnika: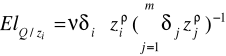
Efekt skali (suma elastyczność jak w modelu Cobb-Douglasa): 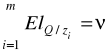
Krańcowa stopa substytucji: 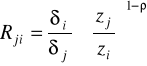
Elastyczność substytucji: 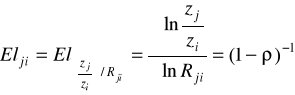
dla Cobba-Douglasa stała i równa 1,
Informuje w przybliżeniu o ile procent wzrasta zj/zi jeśli Rji wzrasta o 1% (mówi o ile powinno wzrosnąć techniczne uzbrojenie pracy, aby krańcowa stopa substytucji wzrosła o 1%)
Metoda Kmenty - historyczna i nienajlepsza, ale pozwalająca oszacować punkty startowe do algorytmu Gaussa-Newtona:
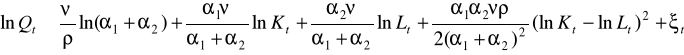
jeżeli oznaczymy kolejno paramtry od beta 0 do beta 3 i oszacujemy zwykłą MNK to otrzymamy punkty startowe:
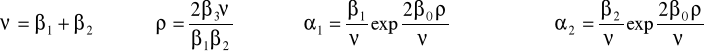
III. Translogarytmiczna funkcja produkcji (Translog)
Liczba swobodnych parametrów:![]()
Funkcja translogarytmiczna nie jest jednorodna ! (brak globalnego efektu skali)
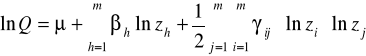
Dwa pierwsze składniki sumy odpowiadają technologii Cobba-Douglasa
Elastyczności najlepiej liczyć z pochodnej logarytmicznej i analogicznie współczynnik efektu skali (sumy elastyczności)
Podobnie produkcyjności krańcowe i elastyczności substytucji:
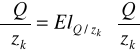
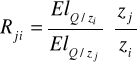
Estymacja funkcji produkcji: - na podstawie danych przekrojowych lub szeregów czasowych
Do Cobba-Douglasa i Translogu wystarczy MNK i KMRL, do CES należy stosować metodę Kmenty i algorytm Gaussa-Newtona
W przypadku CES i Translogu należy jeszcze zweryfikować hipotezę, że model Cobba-Douglasa jest wystarczający:
CES) ![]()
- test t-Studenta dla regresji nieliniowej
wystarczy C-D CES
Translog) ![]()
- test F dla układu współczynników regresji
wystarczy C-D Translog
W przypadku szeregów czasowych bierze się jeszcze pod uwagę postęp techniczno-organizacyjny
![]()
gdzie ⋅ - informuje w przybliżeniu o ile % wzrasta prdukcja z okresu na okres wyłącznie na skutek usprawnień techniczno-organizacyjnych (neutralnego postępu techniczno-organizacyjnego)
Zmienna objaśniająca losowa - stosujemy zwykłą MNK
Regresja liniowa dla danych czasowych - nie można stosować zwykłej MNK dla autokorelacji, ani dla modeli wielorównaniowych, natomiast można zwykłą MNK szacować proces autoregresyjny ze względu na zmienną objaśniającą:
Model autoregresyjny rzędu 1 (AR(1)): ![]()
Modele wielorównaniowe:
Statyczne (bez opóźnień) i dynamiczne (z opóźnieniami)
Yt - wektor zmiennych łącznie współzależnych
Xt - wektor zmiennych ustalonych z góry (wraz z wyrazami wolnymi - kolumna 1)
Ut - wektor równoczesnych składników losowych wszystkich równań
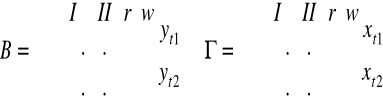
Rodzaje modeli wielorównaniowych:
Proste - macierz B jest macierzą jednostkową; brak bezpośrednich zależności funkcyjnych między bieżącym zmiennymi endogenicznymi
Rekurencyjne - równoczesne składniki losowe róznych równań nie są pomiędzy sobą skorelowane i macierz B jest niejednostkową macierzą trójkątną (lub daje się sprowadzić do trójkątnej prze zamianę numeracji równań i zmiennych i tylko w ten sposób); modeluje wyłącznie jednokierunkowe zależności między bieżącymi zmiennymi endogenicznymi
O równaniach współzależnych - nie jest ani prosty ani rekurencyjny; opisuje dwukierunkowe powiązania między bieżącymi zmiennymi endogenicznymi
Estymacja prostych i rekurencyjnych modeli - zwykła MNK (estymator jest zgodny asymptotycznie)
Postacie modeli:
Strukturalna - układ równań
Zredukowana
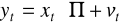
gdzie:
Badanie identyfikalności modelu:
Otrzymujemy układ równań z przemnożenia:
![]()
i - nr kolumny (równania)
Elementy macierzy pi traktujemy jako parametry, parametry modelu jako zmienne
Ze względu na ilość rozwiązań tego układu równań otrzymujemy, że równanie:
Nieidentyfikowalne (układ ma nieskończenie wiele rozwiązań - więcej zmiennych niż równań) - niemożna go estymować
Jednoznacznie identyfikowalne (układ ma dokładnie 1 rozwiązanie - liczba zmiennych jest równa liczbie równań) - pośrednia MNK (jako szczególny przypadek 2MNK)
Niejednoznacznie identyfikowalne (układ jest sprzeczny - więcej równań niż zmiennych) - 2MNK
Pośrednia MNK:
Szacuje się: ![]()
, a parametry równań oblicza się z powyższego układu równań (będą zależne od elementów macierzy
Podwójna MNK:
Dla danego równania wyprowadzamy postać:
![]()
gdzie Y,X,,γ są odpowiednimi macierzami i wektorami tych X,Y,,γ które występują w równaniu, analogicznie składnik losowy; Y ma wymiar T x mi X ma wymiar T x ki
Wyprowdzamy teoretyczne Y: ![]()
tworzymy macierz z: ![]()
Wektor parametrów przy X i Y: 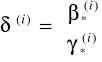
i szacujemy go: ![]()
Błędy średnie szacunku z macierzy: ![]()
a wariancja: 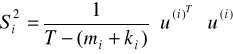
Przy czym teorytyczny składnik losowy jest liczony z równania oryginalnego: ![]()
Można to zapisać gotowymi wzorami:
Analiza mnożnikowa
Uogólniony model regresji liniowej (UMRL)
Copyright SGP
Ekonometria
Rachunek macierzowy:
Mnożenie macierzy (schemat Falka)
Macierz symetryczna (iloczyn transponowany jest zawsze symetryczny)
Macierz diagonalna (na przekątnej liczby, poza nią zera)
Macierz jednostkowa (jw. na przekątnej jedynki)
Macierz trójkątna (pod lub nad przekątną same zera)
Macierz nieosobliwa (gdy wyznacznik macierzy jest różny od zera)
Macierz ortogonalna (gdy iloczyn transponowany równy jest macierzy jednostkowej)
Macierz idenpotentna (gdy kwadrat macierz jest jej równy)
Macierz określona dodatnio (gdy wszystkie minory główne są dodatnie
Trace (ślad) macierzy (suma elementów na przekątnej
Rząd macierzy
Klasyczny model regresji linowej (KMRL):
Założenia normalnie zapisane |
Założenia w rachunku macierzowym |
|
|
|
|
|
|
Składniki losowe poszczególnych obserwacji są między sobą nieskorelowane: |
Szacowanie wartości w KMRL:
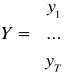
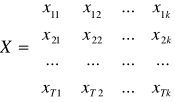
- znane nam 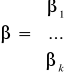
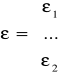
- nieznane
Macierze X,Y dla specyficznych modeli:
Model wielomianowy (może być wyższa potęga niż 2): ![]()
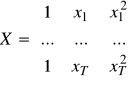
Y - bez zmian
Model hiperboliczny: ![]()
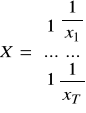
Y - bez zmian
Modele potęgowe i wykładnicze należy zlogarytmować obustronnie i podastawić - dalej regresja liniowa.
Twierdzenie Gaussa i Markowa (estymacja metodą MNK):
^ ^
![]()
z macierzą kowariancji ![]()
^ ^ ^ ^ ^ ^ ^
![]()
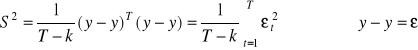
^
przyjmuje się, że: ![]()
błędy ocen parametrów: ![]()
korelacja: 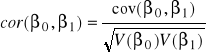
- wartości z macierzy V()
współczynnik zbieżności: 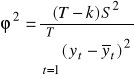
współczynnik determinacji R2=1-2
Klasyczny model normalnej regresji liniowej: (KMNRL):
KMRL + założenie 6: ε ma wielowymiarowy rozkład normalny (Gaussa)
Budowa przedziałów ufności dla parametrów regresji:
^ ^ ^ ^
![]()
gdzie t to rozkład t-studenta o T-k stopniach swobody (![]()
)
Uzyskany przedział liczbowy jest realizacją najkrótszego przedziału o końcach losowych w którym z zadanym prawdopodobieństwem (1-) zawiera się nieznany parametr
Testowanie istotności parametrów regresji:
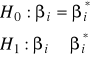
(najczęściej testuje się dla i* = 0 - testowanie istotności wpływu zmiennej objaśniajacej na objaśnianą)
sprawdzian testu: 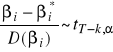
- jeżeli moduł sprawdzianu testu (statystyki) jest większy od wartości krytycznej (t) to odrzucamy H0 na korzyść H1, jeżeli statystyka jest mniejsza od wartości krytycznej to brak podstaw do odrzucenia H0 (zdarzenie wysoce prawdopodobne przy H0); uwaga: dotyczy: testu dwustronnego
Testowanie istotności układu współczynników regresji:
Macierz X dzielimy na dwie części: X=[X1, X2] o wymiarach k1 i k2 (k1+k2=k), analogicznie macierz na (1) i (2)
Model ma wówczas postać: ![]()
![]()
- w H1 zakładamy, że przynajmniej jedna zmienna objaśniająca z X2 ma wpływ na zmienna objaśnianą (Y)
sprawdzian testu: ![]()
- SSEi - suma kwadratów reszt dla Hi, reszta analogicznie
Przypadek szczególny: - model regresji z wyrazem wolnym (macierz X ma kolumnę jedynek)
Testujemy wszystkie parametry regresji z wyjątkiem wyrazy wolnego (k2=k-1) - H0, H1 - jw.
sprawdzian testu: 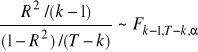
Testowanie stałości wariancji:
Obserwacje, w których spodziewamy się mniejszej S2 grupujemy w Y(1) (wymiary T1 x 1) i odpowiadające im X1 (T1 x k)
Obserwacje, w których spodziewamy się większej S2 grupujemy w Y(2) (wymiary T2 x 1) i odpowiadające im X2 (T2 x k)
Jeżeli T>T1+T2 to pozostałe obserwacje tworzą zbiór środkowy, jeżeli są sobie równe - brak zbioru środkowego
Budujemy dwa modele regresji i szacujemy ich parametry zwykłą MNK oraz liczymy S2 dla obu grup obserwacji.
![]()
sprawdzian testu: 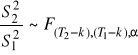
Regresja nieliniowa - algorytm Gaussa - Newtona:
Punkty startowe dobieramy arbitralnie (w praktyce korzystając z jakiegoś przybliżenia)
W kolejnych krokach obliczamy kolejne przybliżenia parametrów:
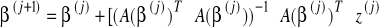
gdzie: 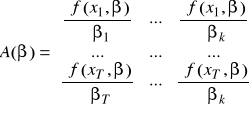
- macierz pochodnych cząstkowych,
a ![]()
- wektor reszt, przy czym 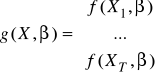
- wektor funkcji rzeczywistych
Sprawdzamy za każdym razem kryterium stopu:
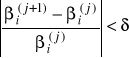
δ - przyjęte kryterium stopu (ustalona mała liczba)
![]()
- bo nie ma różnicy j czy j+1 jeżeli zatrzymaliśmy się na kryterium stopu - statystycznie nierozróżnialne
^ ^ ^ ^ ^ ^
![]()
i ![]()
, gdzie cii = V(); testowanie jak KMRL
I funkcja Törquista (krzywa Engla dla dobra podstawowego):
![]()
po przekształceniach: ![]()
, > 0
dobór punktu startowego:![]()
lub ![]()
elastyczność: ![]()
mówi o ile procent zmieni się Dt przy gdy Mt wzrośnie o 1%
w tym przypadku: ![]()
- interpretacja 2; interpretacja 1 - poziom nasycenia
II funkcja Törquista (krzywa Engla dla dobra wyższego rzędu):
![]()
- poziom nasycenia, γ - poziom od którego można nabyć dane dobro
III funkcja Törquista (krzywa Engla dla dobra luksusowego):
![]()
γ - poziom od którego można nabyć dane dobro, asymptoty ukośne
Ekonometryczne funkcje produkcji:
Definicje charakterystyczne dla procesu produkcji:
Produkcyjność krańcowa i-tego czynnika produkcji
![]()
- informuje nas o ile jednostek wzrasta produkcja (Q), gdy nakład i-tego czynnika (zi) wzrasta o jednostkę przy ustalonych nakładach pozostałych czynników
Powinna spełniać dwa postulaty: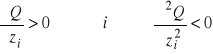
Elastyczność produkcji względem nakładu i-tego czynnika
![]()
- informuje nas w przybliżeniu o ile procent wzrośnie produkcja (%), jeżeli nakład i-tego czynnika produkcji wzrośnie o 1% przy ustalonych nakładach pozostałych czynników
Lokalny współczynnik efektu skali
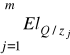
- informuje nas o ile w przybliżeniu wzrośnie produkcja (%), jeżeli nakłady wszystkich czynników produkcji wzrosną naraz o 1%
dla funkcji jednorodnych stopnia lokalny współczynnik efektu skali jest równy globalnemu: 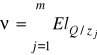
Izokwanty (krzywe / powierzchnie jednakowego produktu) - wszystkie te kombinacje czynników produkcji, które dają w efekcie tę samą produkcję
Krańcowa (techniczna stopa substytucji)
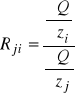
- informuje w przybliżeniu ile dodatkowych jednostek nakładu czynnika j należy zaangażować, aby wycofać jednostkę czynnika i nie zmieniając produkcji (przy ustalonych nakładach pozostałych czynników) - w książce jest odwrotnie R i / j
Funkcje produkcji:
Funkcja Cobba i Douglasa
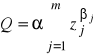
lub 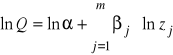
Elastyczność:![]()
Produkcyjność krańcowa: ![]()
Efekty skali (globalny równy lokalnemu): 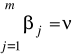
- efekt skali i elastyczności są niezmienne
>1 - rosnący 1 - stały 1 - malejący efekt skali
Izokwanta: 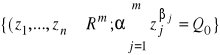
Krańcowa stopa substytucji: 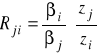
Postać jawna izokwanty dla pracy i kapitału: 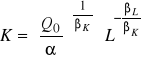
Funkcja o stałej elastyczności substytucji (CES / SMAC)
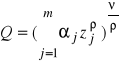
lub 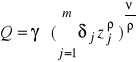
gdzie j>0, η>0, ρ<1 (ρ nie może być zerem) lub 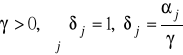
dla ρ=1 - doskonała substytucyjność (prosta)
dla ρ→ funkcja Cobba i Douglasa (![]()
, krzywa)
dla ρ→−∞ - technologia Leontieffa (doskonała komplementarność, wykres - L)
K
L
Zależności w analizie przepływów międzygałęziowych dla gospodarki zamkniętej
popyt pośredni (zużycie pośrednie)
popyt końcowy (równanie podziału)
koszt materiałowy
koszt materialny
całkowity koszt produkcji
zysk
wartość dodana
równanie kosztów
równanie równowagi ogólnej
Tablica PM dla gospodarki zamkniętej
i |
Xi |
1 |
2 |
... |
n |
Yi |
1 |
X1 |
x11 |
x12 |
... |
x1n |
Y1 |
2 |
X2 |
x21 |
x22 |
... |
x2n |
Y2 |
... |
... |
... |
... |
|
... |
... |
n |
Xn |
xn1 |
xn2 |
... |
xnn |
Yn |
|
amortyzacja |
xn+2,1 |
xn+2,2 |
... |
xn+2,n |
|
|
xoj |
x01 |
x02 |
... |
x0n |
|
|
Zj |
Z1 |
Z2 |
... |
Zn |
|
|
Xj |
X1 |
X2 |
... |
Xn |
|
Przykładowa tablica PM
i |
Xi |
1 |
2 |
3 |
Yi |
1 |
500 |
50 |
195 |
0 |
255 |
2 |
300 |
100 |
0 |
90 |
110 |
3 |
150 |
80 |
45 |
15 |
10 |
|
amortyzacja |
15 |
30 |
10 |
|
|
x0j |
200 |
30 |
15 |
|
|
Zj |
55 |
0 |
20 |
|
|
Xj |
500 |
300 |
150 |
|
Tablica PM dla gospodarki otwartej
i |
Xi |
1 |
2 |
... |
n |
Yi(1) |
Yi(2) |
Yi(3) |
Yi(4) |
1 |
X1 |
x11 |
x12 |
... |
x1n |
Y1(1) |
Y1(2) |
Y1(3) |
Y1(4) |
2 |
X2 |
x21 |
x22 |
... |
x2n |
Y2(1) |
Y2(2) |
Y2(3) |
Y2(4) |
... |
... |
... |
... |
|
... |
... |
... |
... |
... |
n |
Xn |
xn1 |
xn2 |
... |
xnn |
Yn(1) |
Yn(2) |
Yn(3) |
Yn(4) |
n + 1 |
import |
xn+1,1 |
xn+1,2 |
... |
xn+1,n |
xn+1(1) |
xn+1(2) |
xn+1(3) |
xn+1(4) |
n + 2 |
amort. |
xn+2,1 |
xn+2,2 |
... |
xn+2,n |
|
|
|
|
|
x0j |
x01 |
x02 |
... |
x0n |
|
|
|
|
|
Zj |
Z1 |
Z2 |
... |
Zn |
|
|
|
|
|
Xj |
X1 |
X2 |
... |
Xn |
|
|
|
|
Oznaczenia:
xn+j,j - koszt materiałów importowanych zużytych w j-tej gałęzi,
Yi(1) - wartość spożycia produktów i-tej gałęzi,
Yi(2) - wartość produktów i-tej gałęzi przeznaczonych na inwestycje,
Yi(3) - wartość produktów i-tej gałęzi przeznaczonych na zapasy,
Yi(4) - wartość eksportu produktów i-tej gałęzi,
xn+1(1) - wartość spożycia produktów z importu,
xn+1(2) - wartość produktów z importu przeznaczonych na inwestycje,
xn+1(3) - wartość produktów z importu przeznaczonych na zapasy,
xn+1(4) - a co to oznacza?
Zależności w analizie przepływów międzygałęziowych dla gospodarki otwartej
koszt materiałowy
koszt materialny
całkowity koszt produkcji
zysk
wartość dodana
równanie kosztów
równanie podziału
równanie równowagi ogólnej
Rachunek dochodu narodowego
amortyzacja
saldo handlu zagranicznego
dochód narodowy wytworzony brutto
dochód narodowy wytworzony netto
dochód narodowy podzielony brutto
dochód narodowy podzielony netto
Wskaźniki efektywności gospodarki
Oznaczenia:
Lj - liczba pracowników zatrudnionych w j-tej gałęzi,
STj - wartość produkcyjnych środków trwałych w gałęzi j-tej.
materiałochłonność
materiałochłonność gospodarki
importochłonność
rentowność
pracochłonność produkcji
wydajność pracy
majątkochłonność produkcji
produktywność majątku trwałego
techniczne uzbrojenie pracy
Model Leontiewa
współczynniki kosztów
macierz struktury kosztów
macierz Leontiewa
model Leontiewa
prognoza I rodzaju lub
prognoza II rodzaju lub
Wprowadzenie do ekonometrii.
Model ekonomiczny i ekonometryczny.
Klasyfikacja modeli ekonometrycznych.
Klasyfikacja ekonometrycznych modeli wielorównaniowych.
1. Czym jest ekonometria?
Ekonometria - zastosowanie metod statystycznych i matematycznych do analizy danych empirycznych, w celu dostarczenia teoriom ekonomicznym materiału empirycznego oraz weryfikacji lub obalenia tych teorii.
2. Prawo popytu
Teoria ekonomiczna: krzywa popytu jest nachylona ujemnie.
Formalizacja teorii ekonomicznej:
q = a + bp, b < 0 lub
q = apb, b < 0, gdzie
q - wielkość popytu, p - cena.
Plaga bogactwa form!
3. Modelowanie
Model - uproszczone przedstawienie rzeczywistych procesów.
Jak szczegółowy powinien być model?
prosty,
złożony.
W praktyce: uwzględniamy w modelu wszystkie czynniki, które uważamy za ważne dla naszego problemu, a pomijamy wszystkie pozostałe.
4. Model ekonomiczny i ekonometryczny
Model ekonomiczny - zbiór założeń, które w przybliżeniu opisują zachowanie się gospodarki.
Model ekonometryczny - formalny opis stochastycznej zależności wyróżnionego zjawiska ekonomicznego (wyróżnionych zjawisk) od czynników, które je kształtują, a wyrażony w formie pojedynczego równania bądź układu równań.
zbiór równań opisujących zachowanie zjawiska ekonomicznego wyprowadzonych z modelu ekonomicznego,
stwierdzenie, czy występują błędy w obserwacjach,
specyfikacja rozkładu prawdopodobieństwa „zakłóceń” oraz ewentualnych błędów w obserwacjach.
5. Prawo popytu
Równanie opisujące zachowanie popytu:
q = a + bp + e,
gdzie e jest czynnikiem zakłócającym.
Specyfikacja rozkładu prawdopodobieństwa e, np. stwierdzenie, że ma rozkład normalny z wartością oczekiwaną 0 i stałą wariancją.
6. Cele ekonometrii
Formułowanie modeli ekonometrycznych, czyli formułowanie modeli ekonomicznych w formie pozwalającej je empirycznie testować.
Estymowanie i testowanie modeli ekonometrycznych na danych obserwacjach.
Wykorzystanie modeli do celów prognostycznych oraz w kreowaniu polityki gospodarczej.
7. Analiza ekonometryczna
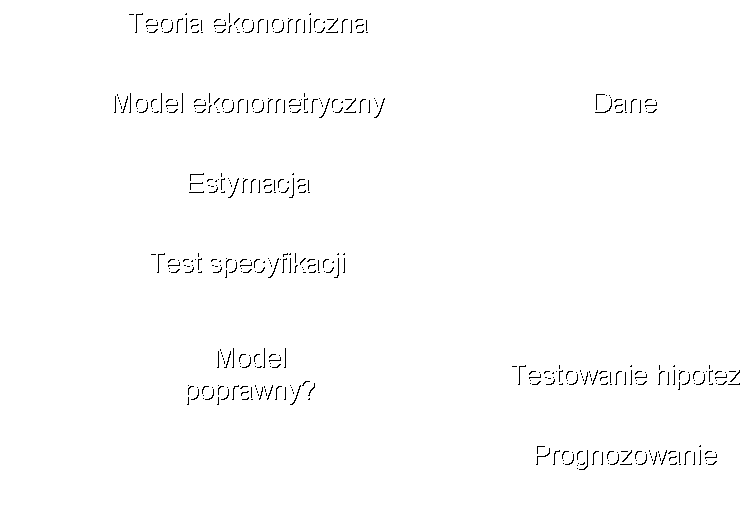
7. Analiza regresji jest narzędziem do opisu i oszacowania ilościowego związku między daną zmienną objaśnianą (zależną), a jedną lub więcej zmiennymi objaśniającymi (niezależnymi).
zmienne objaśniające: x1, x2, ..., xk.
zmienna objaśniana: y
Jeśli k = 1: regresja prosta.
Jeśli k > 1: regresja złożona.
8. Cele stosowania analizy regresji
Analiza efektów zmian wartości pojedynczych zmiennych objaśniających (x'ów).
Prognoza wartości zmiennej objaśnianej (y) dla danego zestawu wartości zmiennych objaśniających (x'ów).
Badanie, czy jakakolwiek zmienna objaśniająca ma istotny wpływ na zmienną objaśnianą.
9. Typy zależności
Funkcyjna zależność y od x:
y = f(x),
gdzie f jest funkcją x.
Zależność
deterministyczna,
stochastyczna.
Zależność liniowa, tj. f(x) jest funkcją liniową:
f(x) = a + bx.
Zależność stochastyczna:
f(x) = a + bx + e,
gdzie e jest „składnikiem losowym” o znanym rozkładzie prawdopodobieństwa.
Dla wielu zmiennych objaśniających:
y = a + a1x1 + a2x2 + ... + akxk + e, gdzie
czynnik deterministyczny: a + a1x1 + a2x2 + ... + akxk,
czynnik stochastyczny: e,
parametry strukturalne: a, a1, a2, ... , ak.
10.Dlaczego uwzględniamy składnik losowy?
Postępowanie podmiotów ekonomicznych cechuje indeterminizm. Oznacza to, że np. ten sam konsument, postawiony wobec takiego samego wyboru w takich samych warunkach, może podjąć każdorazowo nieco inną decyzję.
Pomiar zjawisk jest niedoskonały i niedokładny. Składnik losowy zawiera w sobie różnice wynikające z błędów obserwacji.
Sam model może być wadliwie skonstruowany i w jego specyfikacji brakować może ważnych zmiennych objaśniających lub/i postać funkcyjna może być niepoprawna.
11. Dane do modelu
Podstawowe źródła danych:
publikacje GUS (Roczniki i Biuletyny Statystyczne),
publikacje NBP,
dane finansowe przedsiębiorstw, giełdowe, ...
Szereg czasowy - zestaw liczb odpowiadających wartościom, jakie przybrało rejestrowane zjawisko w kolejnych, jednakowo odległych, momentach czasu (np. latach, kwartałach, miesiącach).
Szereg przekrojowy - dane wyrażające stan zjawiska w ustalonym okresie czasu, ale w odniesieniu do różnych obiektów.
Model ekonometryczny (zapis dla obserwacji):
yt = a + a1tx1 + a2tx2 + ... + aktxk + et, t = 1,...,n
12. Inflacja - szereg czasowy
13. Mieszkania - dane przekrojowe
14. Klasyfikacja zmiennych
Podział na:
A - zmienne endogeniczne: bieżące i opóźnione (wyjaśniane przez model),
B - zmienne egzogeniczne: bieżące i opóźnione (nie wyjaśniane przez model).
Ze względu na rolę pełnioną w modelu:
C - zmienne objaśniane,
D - zmienne objaśniające.
15.Klasyfikacja zmiennych- przykład
Model wielorównaniowy:
PKBt = a0 + a1Zt + a2It-1 + a3It-2 + et1
It = b0 + b1PKBt + et2
Klasyfikacja zmiennych:
A = {PKB, I} B = {Z}
C = {PKBt, It} C = {Zt, It-1, It-2, PKBt}
16.Klasyfikacja modeli ekonometrycznych
KRYTERIUM 1. Liczba równań w modelu:
modele jednorównaniowe,
modele wielorównaniowe.
KRYTERIUM 2. Postać analityczna modelu:
modele liniowe,
modele nieliniowe.
KRYTERIUM 3. Czynnik czasu w modelu:
modele statyczne,
modele dynamiczne.
KRYTERIUM 4. Ogólnopoznawacze cechy modelu:
modele przyczynowo-opisowe,
modele symptomatyczne.
KRYTERIUM 5. Powiązania w modelach wielorównaniowych:
modele proste,
modele rekurencyjne,
modele o równaniach łącznie współzależnych.
17. Dobór zmiennych objaśniających do modelu ekonometrycznego
Y - zmienna objaśniana,
X = {X1, X2, ..., Xm} - zbiór „kandydatek” na zmienne objaśniające,
rij - współczynnik korelacji liniowej Pearsona między „kandydatkami” na zmienne objaśniające,
rj - współczynnik korelacji liniowej Pearsona między zmiennymi Xj i Y,
s = 1, 2, ..., 2m-1 - numer niepustych kombinacji zmiennych ze zbioru X,
Cs - zbiór numerów zmiennych tworzących s-tą kombinację.
18. Metoda Hellwiga
indywidualna pojemność informacyjna nośnika Xj w s-tej kombinacji:
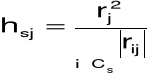
integralna pojemność informacyjna s-tej kombinacji:
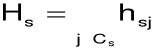
reguła decyzyjna:
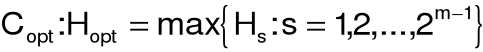
Metoda Najmniejszych Kwadratów (MNK)
Współczynnik determinacji
Koincydencja
Kataliza
Współliniowość zmiennych
1. Jednorównaniowy model ekonometryczny
Y = a0 + a1X1 + a2X2 + ... + akXk + e
yt = a0 + a1x1t + a2x2t + ... + akxkt + et, t = 1,...,n
y = Xa + e
2. Estymatory MNK
wartości teoretyczne:
![]()
![]()
reszta:
![]()
![]()
układ równań normalnych:
XTXa = XTy
estymatory MNK:
a = (XTX)-1XTy
3. Założenia MNK
zmienne objaśniające Xi są nielosowe i nieskorelowane ze składnikiem losowym,
rz(X) = k + 1 £ n,
E(e) = 0,
D2(e) = E(eeT) = s2I, s2 < ¥,
et: N(0,s2), t = 1,2,...,n,
informacje zawarte w próbie są jedynymi, na podstawie których estymuje się parametry strukturalne modelu.
4. Własności estymatorów MNK
Tw. Gaussa - Markowa:
Estymator a wektora parametrów a modelu ekonometrycznego wyznaczony MNK jest estymatorem: liniowym, zgodnym, nieobciążonym i najefektywniejszym w klasie liniowych i nieobciążonych estymatorów.
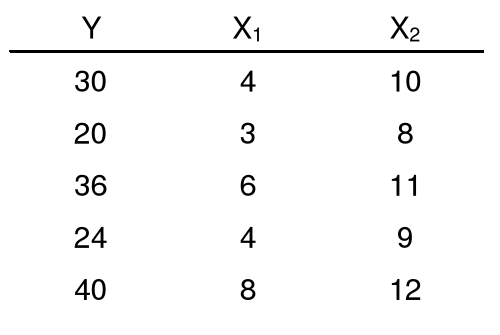
5. Estymator MNK - przykład

![]()
Oszacowanie modelel:
Y - roczna pensja (tysiące $)
X1 - lata nauki po zakończeniu szkoły średniej
X2 - staż pracy w przedsiębiorstwie
6. Własność koincydencji
Model jest koincydentny, jeśli dla każdej zmiennej objaśniającej modelu spełniony jest warunek:
sgn ri = sgn ai
Para korelacyjna:
para (R,R0)
Regularna para korelacyjna: para (R,R0), gdy współczynniki korelacji spełniają warunek:
0 < r1 £ r2 £ ... £ rk
7. Zapis korelacyjny modelu ekonometrycznego
X, Y - dane wystandaryzowane,
R = (1/n)*XTX,
R0 = (1/n)*XTY,
zapis korelacyjny: R0 = Ra + Re,
estymatory: a = R-1R0,
współczynnik determinacji: R2 = R0TR-1R0.
8. Koincydencja - przykład
współczynnik korelacji X1 i X2: r12 = 0,949
model nie jest koincydentny, gdyż
sgn a1 ¹ sgn r1
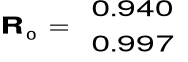
9.Miary jakości modelu
Współczynnik determinacji:
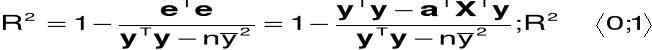
Skorygowany współczynnik determinacji
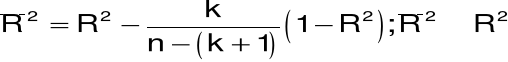
Niescentrowany współczynnik determinacji (model bez wyrazu wolnego)
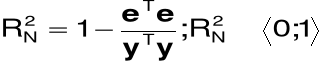
10.Interpretacja R2
Część zmienności zmiennej objaśnianej, która jest wyjaśniana przez model.
Warunki poprawnej interpretacji:
zależność między zmienną objaśnianą, a zmiennymi objaśniającymi jest liniowa,
parametry modelu oszacowane zostały MNK,
model zawiera wyraz wolny.
11.Efekt katalizy
Efekt katalizy - możliwość otrzymania wysokiej wartości współczynnika determinacji mimo, że charakter i siła powiązań zmiennych objaśniających i zmiennej objaśnianej nie uzasadniają takiego wyniku.
Efekt katalizy może mieć miejsce, gdy występuje zmienna - katalizator:
dla regularnej pary korelacyjnej, zmienna Xi z pary (Xi,Xj) jest katalizatorem, jeżeli
rij < 0 lub rij > ri/rj
12.Pomiar zjawiska katalizy
Natężenie zjawiska katalizy:
h = R2 - H,
gdzie H jest integralną pojemnością informacyjną zestawu zmiennych objaśniających.
Względne natężenie efektu katalizy:
Wh = h / R2 x 100%
13. Współliniowość zmiennych
Współliniowość jest wadą próby statystycznej, polegającą na tym, że szeregi reprezentujące zmienne objaśniające są nadmiernie skorelowane.
Konsekwencje występowania współliniowości:
niemożliwy staje się pomiar oddziaływania poszczególnych zmiennych objaśniających,
oceny wariancji estymatorów MNK, związanych ze skorelowanymi zmiennymi, są bardzo duże,
oszacowania parametrów są bardzo wrażliwe na dodanie lub usunięcie z próby niewielkiej liczby obserwacji.
Ale estymatory MNK są BLUE!!!
14. Dokładna współliniowość
Dokładna współliniowość - podzbiór zmiennych objaśniających jest związany zależnością liniową.
rz(X) < k + 1 Þ macierz XTX jest osobliwa i nie istnieją estymatory MNK!
W praktyce: przybliżona współliniowość.
15. Przybliżona współliniowość - co robić?
nie robić nic,
zmienić zakres próby statystycznej,
rozszerzyć model o dodatkowe równania,
nałożyć dodatkowe warunki na parametry,
usunąć zmienną lub zmienne,
wykorzystać wyniki innych badań,
dokonać transformacji zmiennych,
zastosować metodę estymacji grzbietowej,
zastosować metodę głównych składowych.
Weryfikacja statystyczna modelu ekonometrycznego
błędy szacunku parametrów,
istotność zmiennych objaśniających,
autokorelacja,
heteroskedastyczność.
Zmienne zero-jedynkowe
1. Weryfikacja statystyczna modelu
Badanie liniowości modelu
Badanie normalności rozkładu składnika losowego
Badanie autokorelacji składnika losowego
Badanie homoskedastyczności składnika losowego
Badanie istotności zmiennych objaśniających
2. Błędy szacunku parametrów
Macierz kowariancji estymatora a:
D2(a) = s2(XTX)-1
Estymator wariancji s2 składnika losowego:
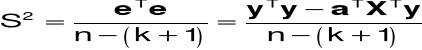
Estymator macierzy kowariancji estymatora a:
![]()
Średni błąd szacunku parametru aj:
![]()
Średni względny błąd szacunku parametru aj:
![]()
3. Przykład
Oszacowany model:
![]()
Oszacowanie wariancji składnika losowego:
S2 = 0.75 S = 0.87
Średnie błędy szacunku dla zmiennej
X1: 0.68
X2: 0.87
Oszacowany model:
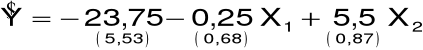
Średnie względne błędy szacunku dla zmiennej
X1: 272%
X2: 16%
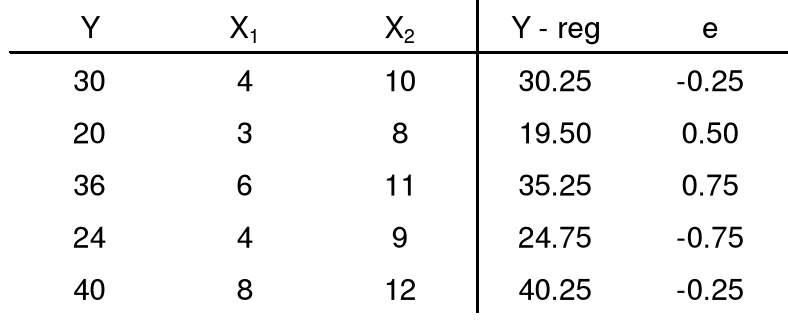
4. Przykład
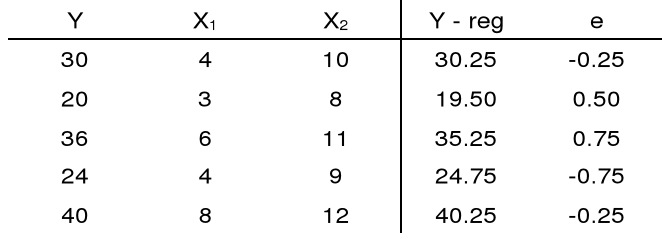
5. Istotność zmiennych objaśniających
Badanie, czy dana zmienna objaśniająca lub zbiór zmiennych objaśniających mają istotny wpływ na zmienną objaśnianą.
Istotność pojedynczej zmiennej - test t-Studenta:
Para hipotez:
H0: aj = 0,
H1: aj ¹ 0.
Statystyka testowa
![]()
: ma rozkład t-Studenta z n = n - (k + 1) stopniami swobody.
Wnioskowanie:
jeśli |t| > ta,n Þ odrzucamy H0 Þ zmienna Xj jest istotna,
jeśli |t| £ ta,n Þ nie ma podstaw do odrzucenia H0 Þ zmienna Xj jest nieistotna
6. Przykład
Oszacowany model:
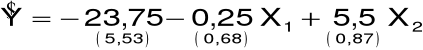
Liczba stopni swobody: n = 2.
Poziom istotności: a = 0,05.
Wartość krytyczna: t0.05;n = 4,3027.
Wartości testowe:
X1: -0,37,
X2: 6,35.
Zmienne istotne: tylko X2.
7. Istotność zmiennych objaśniających
Istotność zmiennych - test F:
Para hipotez:
H0: a1 = a2 = ... = ak = 0,
H1: a1 ¹ 0 lub a2 ¹ 0 lub ... lub ak ¹ 0.
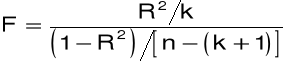
Statystyka testowa:
ma rozkład F-Snedecora z r1 = k i r2 = n - (k + 1) stopniami swobody.
Wnioskowanie:
jeśli F > Fa,r1,r2 Þ odrzucamy H0 Þ przynajmniej jedna zmienna objaśniająca
jest istotna,
jeśli F £ Fa,r1,r2 Þ nie ma podstaw do odrzucenia H0 Þ żadna zmienna
objaśniająca nie jest istotna.
8. Przykład
Liczba stopni swobody licznika: r1 = 2.
Liczba stopni swobody mianownika: r2 = 2.
Wartość krytyczna: F0,05;2;2 = 19,00
Statystyka testowa: F* = 180,33.
Wniosek: R2 jest istotne.
9. Autokorelacja składników losowych
model standardowy, ale D2(e) = F = s2W.
Autokorelacja składników losowych - sytuacja, gdy składniki losowe dotyczące różnych obserwacji są skorelowane, a więc gdy macierz W nie jest diagonalna.
Przyczyny autokorelacji:
natura niektórych procesów gospodarczych,
psychologia podejmowania decyzji,
niepoprawna postać funkcyjna modelu,
wadliwa struktura dynamiczna modelu,
pominięcie w specyfikacji modelu ważnej zmiennej,
zabiegi na szeregach czasowych
10. Schemat autoregresyjny pierwszego rzędu: AR(1)
Założenia:
stacjonarny proces stochastyczny,
homoskedastyczność.
Macierz kowariancji składników losowych
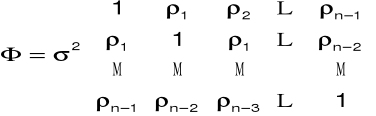

11. Schemat autoregresyjny pierwszego rzędu: AR(1)
Założenie:
et = ret-1 + ht, gdzie
r - współczynnik autokorelacji,
h - składnik losowy spełniający: E(h) =0, D2(h) = sh2I.
Wariancja składnika losowego:
D2(et) = s2 = sh2/(1 - r2)
Macierz kowariancji składników losowych:
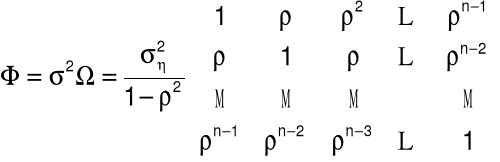
12. Skutki autokorelacji
Estymator MNK jest nieefektywny, ale jest nieobciążony.
Estymator wariancji estymatorów MNK jest obciążony.
Średnie błędy szacunku są niedoszacowane.
Wartości statystyk t są przeszacowane.
Przeszacowany jest współczynnik determinacji.
13. Uogólniona MNK
Założenie: D2(e) = s2W i wszystkie parametry są znane.
Estymator UMNK (estymator Aitkena) jest BLUE:
a = (XTW-1X)-1XTW-1y
W przypadku procesu AR(1):

14. Estymatory współczynnika autokorelacji
współczynnik korelacji reszt
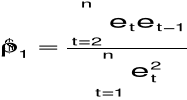
skorygowany współczynnik korelacji reszt:
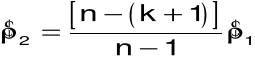
estymator nieobciążony
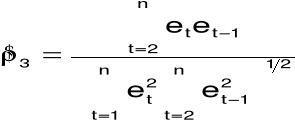
15. Testowanie zjawiska autokorelacji
Test Durbina-Watsona
Para hipotez:
H0: r = 0,
H1: r > 0 (jeśli est. r > 0) lub r < 0 (jeśli est. r < 0).
Statystyka testowa:
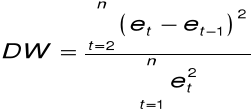
16. Przykład
Statystyka testowa: DW = 2,083.
0
dL = 0,946
dU = 1,543
4 - dU = 2,457
4 - dL = 3,054
4
Wniosek: brak autokorelacji.
17. Heteroskedastyczność
Heteroskedastyczność - zjawisko polegające na niejednorodności wariancji składników losowych w obrębie próby. Elementy leżące na głównej przekątnej macierzy F = D2(e) nie są jednakowe.
Skutki heteroskedastyczności:
estymatory MNK są nieefektywne, ale nieobciążone i zgodne,
obciążone są estymatory wariancji estymatorów parametrów strukturalnych.
18. Testowanie heteroskedastyczności
Test Goldfelda - Quandta
Para hipotez:
H0: s12 = s22,
H1: s12 ¹ s12.
Statystyka testowa:
19. Przykład
Pierwsza podpróba: obserwacje 1 - 15 i 35 - 50.
Druga podpróba: obserwacje 16 - 34.
Ocena wariancji I: 277100,40.
Ocena wariancji II: 1739,40.
Statystyka testowa: 159,31.
Wartość krytyczna: 2,15.
Wniosek: wariancje w podpróbach są istotnie różne, zatem występuje heteroskedastyczność.
20. Zmienne zero - jedynkowe
Zmienna zero -jedynkowa - zmienna, która przyjmuje tylko dwie wartości jeden lub zero.
Wykorzystywane są do:
zastępowania zmiennych niemierzalnych,
wyróżniania pewnych okresów,
...
UWAGA: Możliwa dokładna współliniowość!
Prognozowanie na podstawie jednorównaniowego modelu ekonometrycznego
prognoza punktowa,
prognoza przedziałowa.
Modele nieliniowe.
Funkcja produkcji.
1. Klasyfikacja prognoz
Prognozowanie ekonometryczne - wnioskowanie o przyszłych wartościach zmiennej endogenicznej na podstawie modelu wyjaśniającego kształtowanie się tej zmiennej.
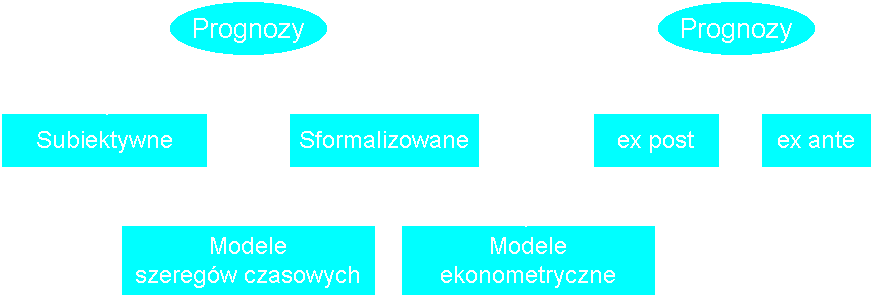
2. Prognoza punktowa
Oszacowany model ekonometryczny
![]()
Okres prognozy: t > n.
Wektor wartości zmiennych objaśniających dla okresu prognozy:
![]()
Prognoza punktowa:
![]()
Średni błąd predykcji ex ante:
![]()
Względny średni błąd predykcji ex ante:
![]()
3. Przykład
Oszacowany model:
![]()
Okres prognozy: t = 6.
Wartości zmiennych objaśniających:
x16 = 5,
x26 = 12.
Prognoza punktowa:
![]()
Średni błąd predykcji ex ante:
![]()
Względny średni błąd predykcji ex ante: v6 = 2,24%
4. Prognoza przedziałowa

Przedział ufności:
![]()
![]()
Prognoza punktowa w przypadku autokorelacji
(t = n + s):
![]()
5. Przykład
Poziom istotności: a = 0,05.
Liczba stopni swobody: u = 2.
Wartość krytyczna: t0,005;2 = 4,303.
Prognoza przedziałowa: (37,04 ; 44,96)
6. Dokładność prognoz ex post
średni absolutny błąd predykcji:
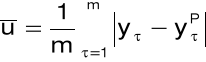
współczynnik Theila:
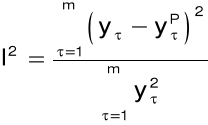
7. Modele liniowe
mają prostą interpretację,
często stanowią dobrą aproksymację relacji nieliniowych,
są łatwe w estymacji oraz weryfikacji statystycznej,
są postacią modeli nieliniowych po ich linearyzacji.
8. Nieliniowości modeli
Modele nieliniowe względem zmiennych:
np. Y = a0 + a1X + a2X2 + e,
proste, bo podstawiamy Z = X2 i Y = a0 + a1X + a2Z + e.
Modele nieliniowe względem parametrów
np. Y = a0 + a12X + a2Z + e,
trudne metody estymacji,
czasami pomaga linearyzacja modelu,
sprawdzian: jeśli każda pochodna cząstkowa zmiennej Y względem parametrów modelu jest niezależna od wszystkich parametrów modelu, to taki model jest liniowy względem parametrów.
9. Typowe modele nieliniowe
Model wielomianowy:
Y = a0 + a1X + a2X2 + ... + akXk + e.
Model logarytmiczny: Y = a0 + a1lnX + a2lnZ + e.
Model hiperboliczny: Y = a0 + a1/X + a2Z + e.
Model z interakcjami:
Y = a0 + a1X + a2Z + a3XZ + e.
![]()
Model potęgowy:
Model wykładniczy:
![]()
Model S-krzywej:
![]()
10. Funkcja produkcji
Funkcja produkcji - zależność między nakładami czynników produkcyjnych w pewnym procesie, a wielkością wytworzonego produktu.
Ekonometryczna funkcja produkcji - model jednorównaniowy, w którym zmienną objaśnianą jest produkcja Y, a zmiennymi objaśniającymi są nakłady J czynników produkcji Xj:
Y = f(X1,X2,...,XJ)
Nakłady:
kapitału:K,
pracy: L.
11. Założenia o funkcji produkcji
Funkcja produkcji: Y = f(K,L).
Założenia:
Y > 0, K > 0, L > 0,
izokwanty produkcji (linie stałego produktu), tj. linie którym odpowiada ta sama wartość produkcji, czyli Y0 = f(K,L), są wypukłe,
funkcja produkcji jest ciągła i dwukrotnie różniczkowalna.
12. Własności funkcji produkcji
Produkcyjność krańcowa czynnika produkcji jest dodatnia:
fK > 0, fL > 0.
Produkcyjność krańcowa czynnika jest malejąca:
fKK < 0, fLL < 0.
Krańcowa produkcyjność jednego czynnika wzrasta w miarę zwiększania nakładów drugiego czynnika:
fKL > 0, fLK > 0.
12. Własności funkcji produkcji
Funkcja f jest jednorodna:
f(lK,lL) = lrf(K,L),
r = 1 - stałe korzyści skali,
r > 1 - rosnące korzyści skali,
r < 1 - malejące korzyści skali.
Czynniki produkcji są wzajemnie zastępowalne:
KSS = dK/dL = - fL/fK - substytucja pracy przez kapitał.
13. Funkcja Cobba - Douglasa
Wieloczynnikowa funkcja produkcji Cobba - Douglasa:
![]()
Dwuczynnikowa funkcja produkcji Cobba - Douglasa:
Y = aKbLce, a > 0, b > 0, c >0,
produkcyjności krańcowe są dodatnie:
fK = abKb - 1L > 0, fL = acKbLc -1 > 0,
produkcyjności krańcowe są malejące:
fKK = ab(b - 1)Kb -2Lc < 0, fLL = ac(c -1)KbLc - 2 < 0,
produkcyjność jednego czynnika rośnie przy zwiększaniu nakładów drugiego: fKL = fLK = abcK b - 1 L c - 1 > 0,
14. Dwuczynnikowa funkcja produkcji Cobba - Douglasa
funkcja jest jednorodna stopnia b + c:
f(lK,lL) = l b + c f(K,L), 1 - alfa
krańcowa stopa substytucji:
KSS = - c/b * K/L,
efektywność produkcji względem nakładów czynników produkcji są stałe:
EKY = b, ELY = c.
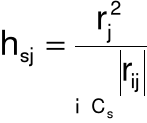
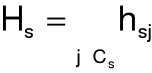
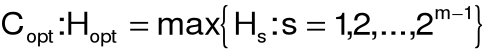
![]()
![]()
![]()
![]()
![]()
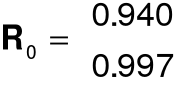
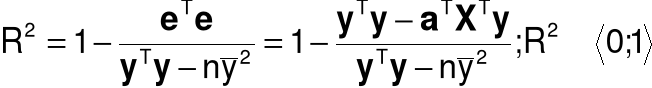
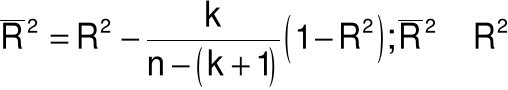
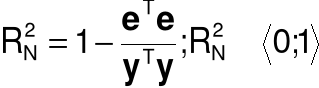
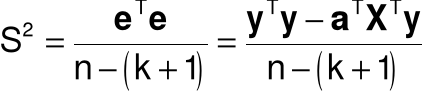
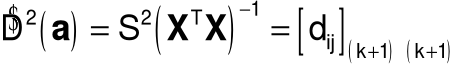
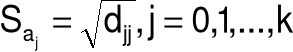

![]()
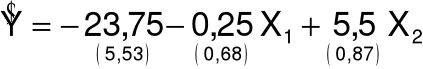
![]()
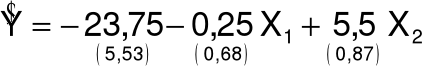
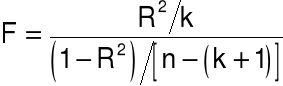
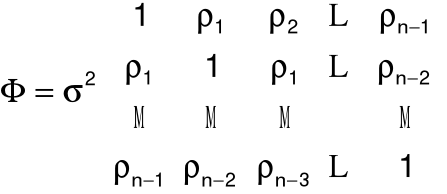
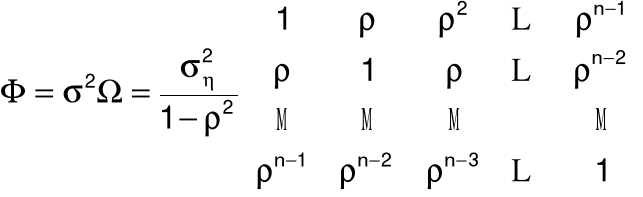

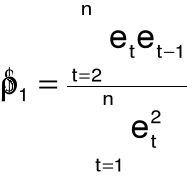
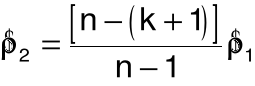
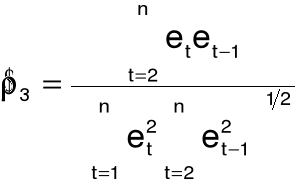
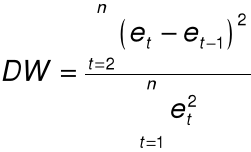
![]()
![]()
![]()
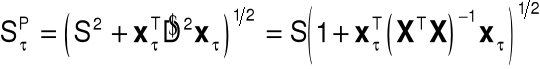
![]()
![]()
![]()
![]()

![]()
![]()
![]()
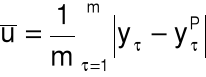
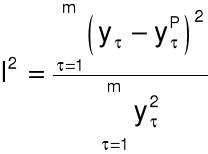
![]()
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
Ekonometria wzory cz.1, EKONOMETRIA
ekonomia wzory
ekonometria wzory 2, Ekonometria
ekonometria, Ekonometria-wzory2, EKONOMETRIA - WZORY
EKONOMETRIA WZORY 3 STR , Inne
EKONOMETRIA WZORY KOLOS II
Geografia ekonomiczna - testy, Szkoła, wypracowania, ściągi
analiza ekonomiczna ściąga, SZKOŁA, FINANSE i rachunkowość, finanse
Analiza ekonomiczna wzory
ekonometria - wzory (3 str), Ekonomia, ekonomia
geografia ekonomicznaPierwsze 16stron, SZKOŁA, szkola 2011
Analiza ekonomiczna - wzory
więcej podobnych podstron