Wstęp:

Efekt Halla polega na powstawaniu poprzecznego pola elektrostatycznego do kierunku natężenia prądu I przepływającego przez np. półprzewodnik, który został umieszczony w polu magnetycznym o indukcji B prostopadłej do kierunku płynącego prądu I. W wyniku powstawania poprzecznego pola elektrycznego następuje spadek potencjału poprzeczny do kierunku przewodzenia, co w konsekwencji doprowadza do utworzenia tzw. napięcia Halla.

Cel ćwiczenia:

- zbadanie efektu Halla w germanie

- wyznaczenie stałej Halla, koncentracji i ruchliwości nośników prądu w badanej próbce

- określenie typu przewodnictwa w badanej próbce

Sprzęt wykorzystany do pomiarów:

- obwód zasilania badanej próbki

- miernik natężenia prądu

- miernik napięcia Halla

- elektromagnes

- sonda do pomiaru indukcji B ( Hallotron)

- miernik indukcji pola magnetycznego (Teslametr)

Przebieg doświadczenia:

Po zapoznaniu się z elementami układu pomiarowego, przystąpiłem razem z zespołem do przeprowadzenia czterech pomiarów wartości natężenia I oraz napięcia Halla przy stałej indukcji B pola magnetycznego.

Wyniki pomiarów zostały przedstawione w poniższych tabelach oraz na wykresach:

B	[mT]	100
I	[mA]	-30	-25	-20	-15	-10	-5	0	5	10	15	20	25	30
UH	[mV]	94	89	83	78	74	68	62	57	52	47	42	36	32

a = -1,0428572 Tm² ∆ a = 0,007372 Tm²

B	[mT]	250
I	[mA]	-30	-25	-20	-15	-10	-5	0	5	10	15	20	25	30
UH	[mV]	127	117	107	95	86	76	63	52	44	33	23	13	3

a = -2,081319 Tm² ∆ a = 0,014921 Tm²

B	[mT]	-100
I	[mA]	-30	-25	-20	-15	-10	-5	0	5	10	15	20	25	30
UH	[mV]	50	52	54	56	58	60	61	63	65	67	68	70	72

a = 3,604396 x 10^-1 Tm²
∆ a = 0,048696 x 10^-1 Tm²

B	[mT]	-250
I	[mA]	-30	-25	-20	-15	-10	-5	0	5	10	15	20	25	30
UH	[mV]	20	26	34	40	46	54	61	68	74	81	88	94	99

a = 1,343956 Tm² ∆ a = 0,011644 Tm²

Następnie przystąpiłem z zespołem do pomiarów wartości indukcji B pola magnetycznego oraz napięcia Halla dla czterech róznych wartości natężenia prądu I przepływającego przez badaną próbkę.

Wyniki pomiarów przedstawione zostały w poniższych tabelach oraz na wykresach:

I	[mA]	30
B	[mT]	-250	-200	-150	-100	-50	0	50	100	150	200	250
UH	[mV]	101	91	81	71	62	52	42	32	22	13	4

a = -1,949091 x 10^-1 Tm²
∆ a = 0,008485 x 10^-1 Tm²

I	[mA]	15
B	[mT]	-250	-200	-150	-100	-50	0	50	100	150	200	250
UH	[mV]	81	76	71	66	62	57	52	47	43	38	34

a = -9,436364 x 10^-2 Tm²

∆ a = 0,071453 x 10^-2 Tm²

I	[mA]	-15
B	[mT]	-250	-200	-150	-100	-50	0	50	100	150	200	250
UH	[mV]	40	45	50	56	62	67	73	79	84	90	95

a = 1,116364 x 10^-1 Tm²

∆ a = 0,007273 x 10^-1 Tm²

I	[mA]	-30
B	[mT]	-250	-200	-150	-100	-50	0	50	100	150	200	250
UH	[mV]	20	30	41	51	61	73	83	94	105	116	127

a = 2,143636 x 10^-1 Tm²

∆ a = 0,010825 x 10^-1 Tm²

Opracowanie wyników pomiarów

• Wyznaczanie stałej Halla, koncentracji i ruchliwości nośników prądu w badanej próbce dla :

a) B=const.

b) I=const.

a)

- B=100 mT:

- B=250 mT:

- B= -100 mT:

- B= -250 mT:

b)

- I= 30 mA

- I=15 mA

- I= -15 mA

- I= -30 mA

• Wyznaczanie ∆R_h ze wzoru:

1. dla B = const.:

gdzie:

R_H = -0,069 m³*C^-1

a = -0,355 Tm²

∆a = 0,0207 Tm²

S = 1,0*10^-5 m²

∆S = 0,1*10^-5 m²

B_śr.= 0 mT

∆B_śr.= 0 mT

d = 1,0*10^-3 m

∆d = 0,1*10^-3 m

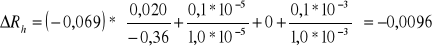
2. dla I = const.:

gdzie:

R_H = -0,0685 m³*C^-1

a = 1,036*10^-2 Tm²

∆a = 8,432*10^-4 Tm²

S = 1,0*10^-5 m²

∆S= 0,1*10^-5 m²

I_{śr .}= 0 mA

∆I_śr. = 0 mA

d = 1,0*10^-3 m

∆d = 0,1*10^-3 m

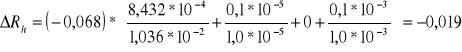
Średnia arytmetyczna:

m³*C^-1

• Wyznaczanie średniej wartości stałej Halla:

a) dla B = const.

Wartość stałej Halla	Rh
1.	-0,104
2.	-0.083
3.	-0,036
4.	-0,054

Średnia wartość R_h = (-0,069
0,014) m³ *C^-1

b) dla I = const.

Wartość stałej Halla	Rh
1.	-0,065
2.	-0,063
3.	-0,075
4.	-0,071

Średnia wartość R_h = (-0,068
0,014) m³ *C^-1

Średnia arytmetyczna:

m³ *C^-1

Wynik końcowy:

• Wyznaczanie średnich i błędów średnich pomiarów metodą Studenta-Fishera:

a) koncentracji nośników prądu:

- dla B=const.

Współczynnik n	n
1.	0,59*10^20
2.	0,75*10^20
3.	1,72*10^20
4.	1,15*10^20

Średnia wartość n = (1,05*10²⁰
0,60) m^-3

α = 0,9 poziom istotności

S_n = 0,25173

∆ n = S_n*k_α

∆ n = 0,25173 *2,353 = 0,60 m^-3

- dla I=const.

Współczynnik n	n
1.	0,96*10^20
2.	0,99*10^20
3.	0,83*10^20
4.	0,83*10^20

Średnia wartość n = (0,90*10²⁰
0,10) m^-3

α = 0,9 poziom istotności

S_n = 0,04230
∆ n = S_n*k_α

∆ n = 0,4230 *2,353 = 0,10 m^-3

Śrenia arytmetyczna

m^-3

m^-3

Wynik końcowy:

n = (0,98*10²⁰
0,35) m^-3

b) ruchliwości nośników prądu:

- dla B=const.

Współczynnik μ	μ
1.	3,92
2.	3,12
3.	1,36
4.	2,04

Średnia wartość μ = (2,61
1,34)

α = 0,9 poziom istotności

S_μ = 0,567421
∆ μ = S_μ *k_α

∆ μ = 0.567421*2,353 = 1,34

- dla I=const.

Współczynnik μ	μ
1.	2,45
2.	2,38
3.	2,83
4.	2,84

Średnia wartość μ = (2,63
0,28)

α = 0,9 poziom istotności

S_μ = 0,122099
∆ μ = S_μ *k_α

∆ μ = 0,122099*2,353 = 0,28

Średnia arytmetyczna:

Wynik końcowy:

=(2,62
0,81)

Wnioski:

Napięcie Halla jest wprost proporcjonalne zarówno do natężenia prądu przepływającego przez badaną próbkę jak i do wektora indukcji B pola magnetycznego, w którym próbka została umieszczona. Ujemny znak przed wartością stałej Halla, którą wyznaczyłem wraz z zespołem sygnalizuje że nośnikami prądu w badanej próbce są elektrony, dlatego moim zdaniem badana próbka jest metalem.

---