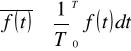
8. Wielkości charakteryzujące sygnały okresowe

1. Wartością chwilową sygnału nazywamy wartość, jaką przyjmuje sygnał w danej chwili (np. f(t), i(t), u(t)).

2. Wartością średnią całookresową sygnału okresowego o okresie T nazywamy średnią arytmetyczną tego sygnału obliczoną dla jednego okresu T.

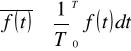
3. Wartością skuteczną sygnału okresowego o okresie T nazywamy pierwiastek kwadratowy z wartości średniej kwadratu sygnału obliczonej dla jednego okresu T.

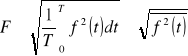
4. Wartością wyprostowaną nazywamy średnią z modułu sygnału.

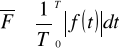
5. Współczynnikiem szczytu sygnału okresowego nazywamy stosunek wartości maksymalnej (szczytowej)
sygnału do jego wartości skutecznej F.

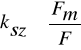
np: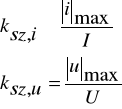

6. Współczynnikiem kształtu sygnału okresowego nazywamy stosunek wartości skutecznej sygnału F do jego wartości średniej
.

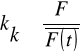
np: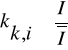

Współczynniki szczytu oraz kształtu prądu i napięcia sinusoidalnego

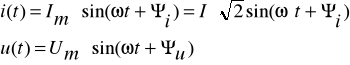
Wartości skuteczne: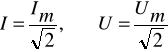

Wartości wyprostowane: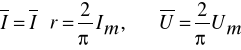

Stąd:

Współczynniki szczytu, oraz współczynnik kształtu

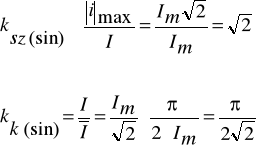
Zadanie 1. Oblicz wartość prądu: średnią, skuteczną i wyprostowaną oraz wartości współczynnika szczytu i współczynnika kształtu dla funkcji okresowej przedstawionej na poniższym rysunku.

równanie prostej

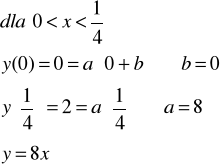
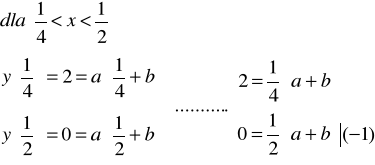
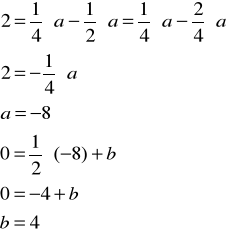
Stąd

dla

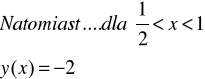
- Wartość średnia prądu:

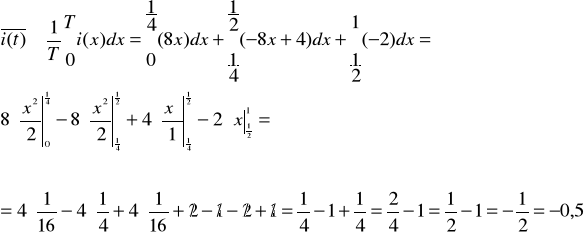
I - Wartość skuteczna prądu:

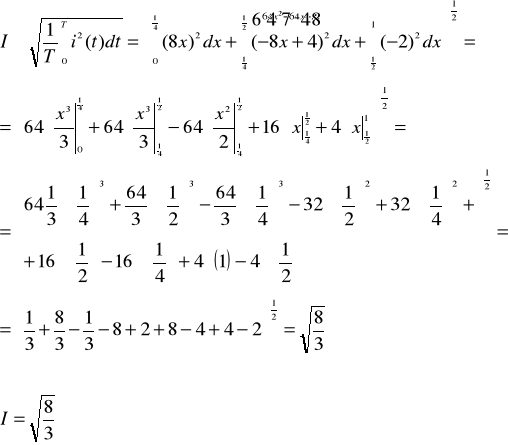
- Wartość wyprostowana prądu

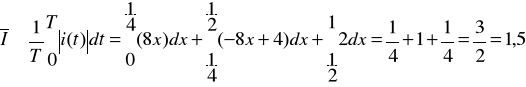
- Współczynnik szczytu prądu

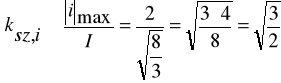
- Współczynnik kształtu prądu

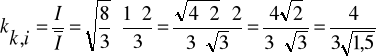
II Wersja:

Wartość średnia prądu

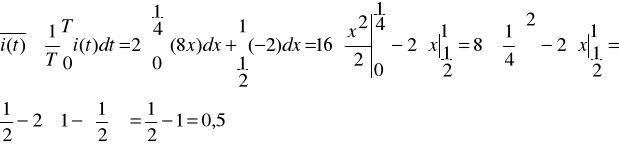
Wartość skuteczna prądu

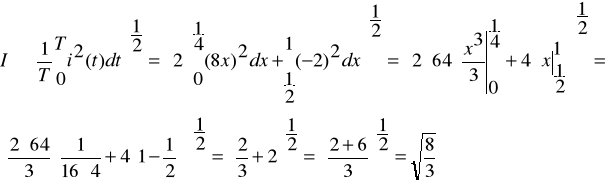
Wartość wyprostowana prądu

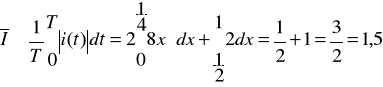
- Współczynnik szczytu prądu

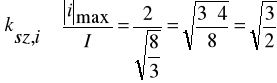
- Współczynnik kształtu prądu

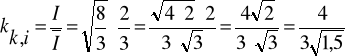
Zadanie 2. Oblicz wartość napięcia: średnią, skuteczną i wyprostowaną oraz wartości współczynnika szczytu i współczynnika kształtu dla funkcji okresowej przedstawionej na poniższym rysunku.

Wartość średnia napięcia

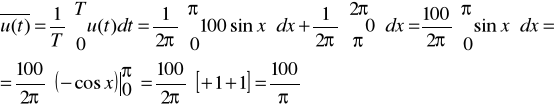
Wartość skuteczna napięcia

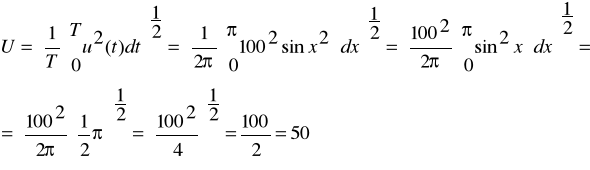
Ponieważ

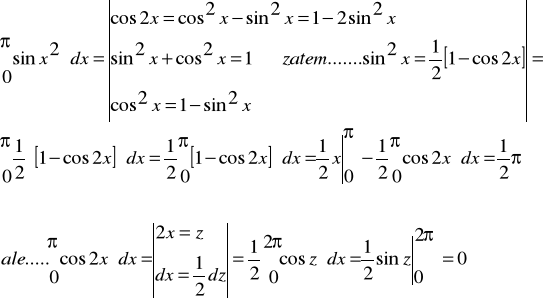
x	0	π
z	0	2 π

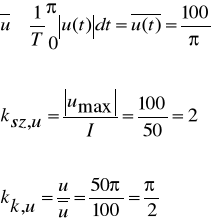
Zadanie 3. Oblicz wartości napięcia: skuteczne i średnie półokresowe oraz wartości szczytu i kształtu dla funkcji okresowej przedstawionej na poniższym rysunku.

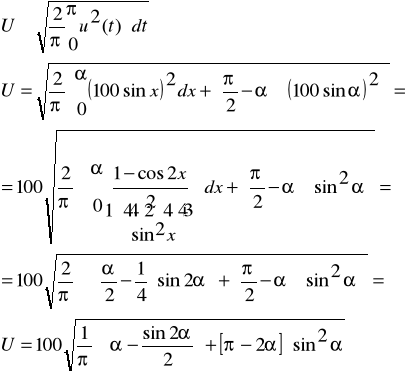
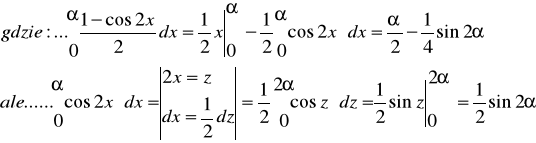
x	0	α
z	0	2 α

Zadanie 4. Oblicz wartości skuteczne i wartości wyprostowane oraz wartości współczynników szczytu i kształtu dla funkcji okresowej przemiennej przedstawionej na poniższym rysunku.

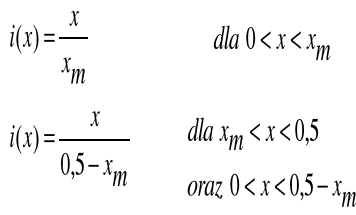
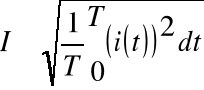
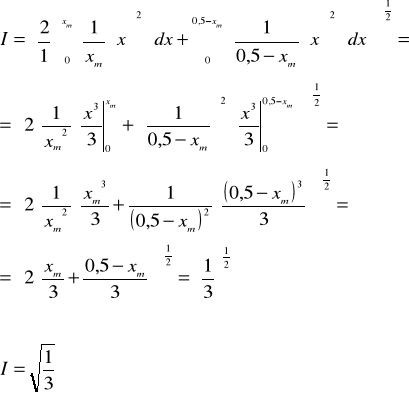
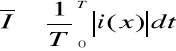
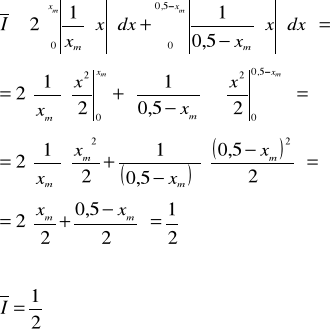
- Współczynnik szczytu

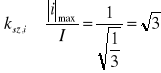
- Współczynnik kształtu

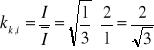
Wniosek:

Parametr x_m nie wpływa na

Zadanie 5. Oblicz wartości skuteczne, wartości średnie półokresowe oraz wartości współczynnika szczytu i kształtu dla funkcji okresowej antysymetrycznej przedstawionej na poniższym rysunku.

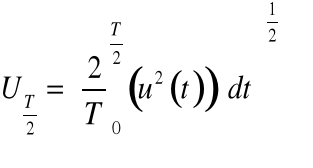
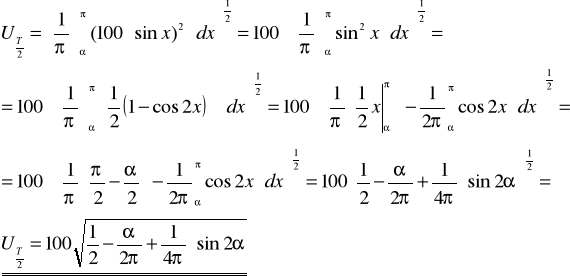
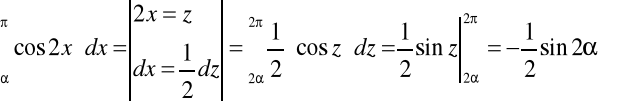
x	α
z	2 α	2

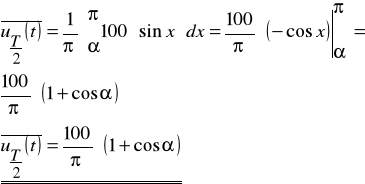
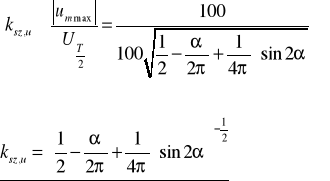
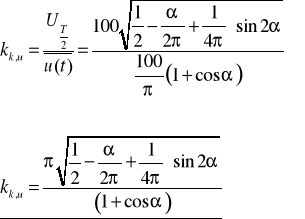
Zadanie 6. Oblicz wartość skuteczną, wartość średnią półokresową oraz wartość współczynnika szczytu i kształtu dla funkcji okresowej antysymetrycznej przedstawionej na poniższym rysunku.

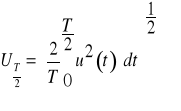
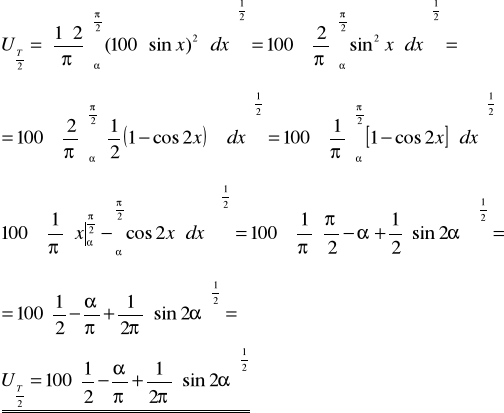
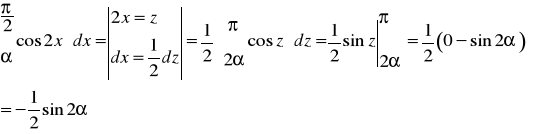
x
z	2

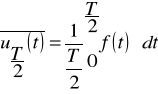
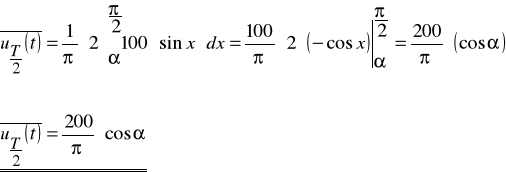
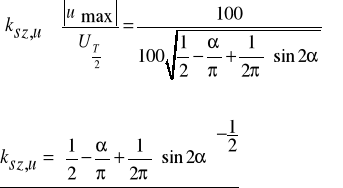
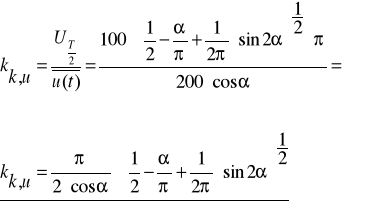
9. Dwójniki prądu sinusoidalnego

Przebiegi sinusoidalne prądu i napięcia dwójników zapisuje się w postaci

i(t) = Im sin(ωt + Ψi) gdzie: i(t) - wartość chwilowa prądu, Im - wartość maksymalna prądu, Ψi - kąt przesunięcia fazowego prądu gdzie: u(t) - wartość chwilowa napięcia, Um - wartość maksymalna napięcia, Ψu - kąt przesunięcia fazowego napięcia gdzie: - wartość chwilowa mocy

Rachunek symboliczny

gdzie: X - reaktancja,

X_L - reaktancja indukcyjna,

X_C - reaktancja pojemnościowa.

dla f=50Hz

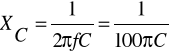
Zadanie 1. Wyznacz przebiegi czasowe prądu dwójnika i(t) oraz narysuj wykresy wskazowe jeżeli dane są wartości elementów i napięcie zasilające.

Dane: R = 50Ω, L = 92mH = 92*10^-3H,

,
,
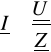
V

,....
,
,

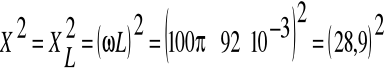
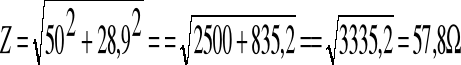
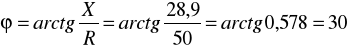
czyli

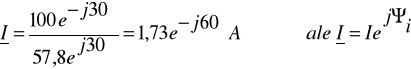
Zadanie 2. Wyznacz przebiegi czasowe prądu dwójnika i(t) oraz narysuj wykresy wskazowe jeżeli dane są wartości elementów i napięcie zasilające.

Dane: R = 50Ω, C = 36,8μF = 36,8*10^-6F,

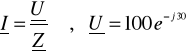
V

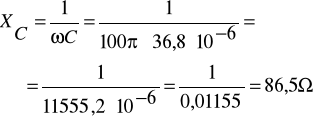
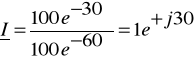
A
[A]

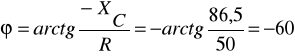
Zadanie 3. Wyznacz przebiegi czasowe prądu dwójnika i(t) oraz narysuj wykresy wskazowe jeżeli dane są wartości elementów i napięcie zasilające.

Dane: R = 50Ω, L = 92mH = 92*10^-3H, C=36,8μF = 36,8*10^-6F,

,

,
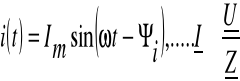
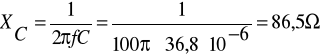
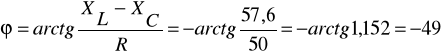
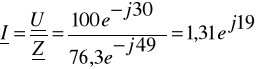
[A],
[A]

Zadanie 4. Dane są wartości elementów R = 50Ω, X_L = 28,9 Ω i X_C = -57,6 Ω tworzących dwójnik (układ gałęzi równoległych), oraz przebieg czasowy występującego na nim napięcia
. Wyznacz przebiegi czasowe: i₁(t), i₂(t) oraz i(t).

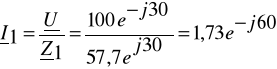
[A]

[A]

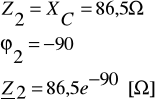
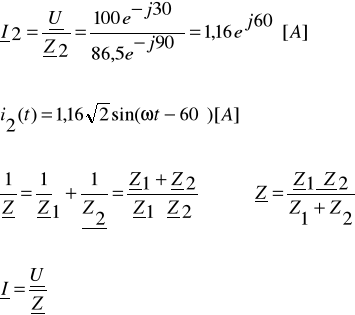
cos(-30º)=cos30º sin(-30º)=-sin30º

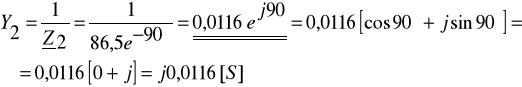
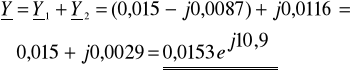
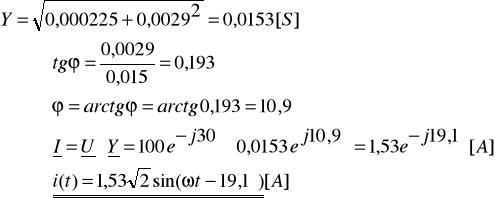
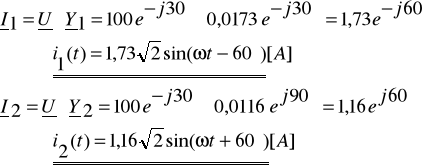
Zadanie 5. Dane są wartości elementów R₁ = 50Ω, R₂ = 50Ω, X₁ = X_L = 28,9Ω i X₂ = X₂- 57,6 Ω tworzących dwójnik (układ gałęzi równoległych), oraz przebieg czasowy występującego na nim napięcia
, f=50Hz. Wyznacz przebiegi czasowe prądów i₁(t), i₂(t), i(t). Narysuj wykresy wskazowe.

[A]

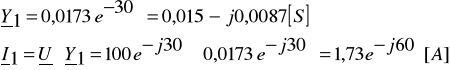
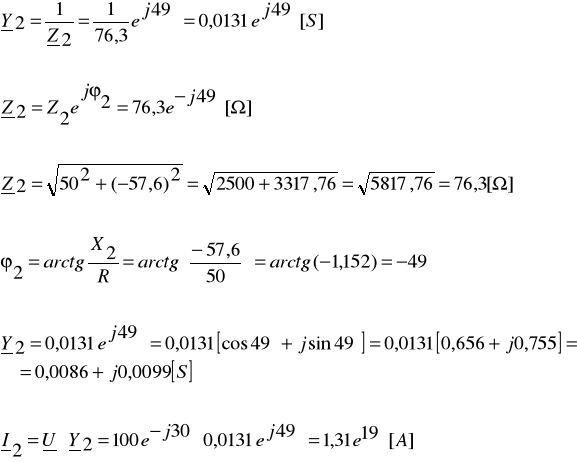
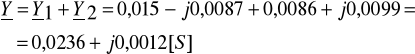
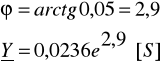
Zadanie 6. Dane są wartości rezystancji R₁ = 30Ω, R₂ = 40Ω i reaktancji X_L = 40Ω, X_C = 30Ω elementów dwójnika (układ równoległy) oraz przebieg czasowy prądu całkowitego
. Określ przebiegi czasowe prądu i₁(t), i₂(t) oraz i(t) wykorzystując wzory dla dzielnika prądu.

analogicznie

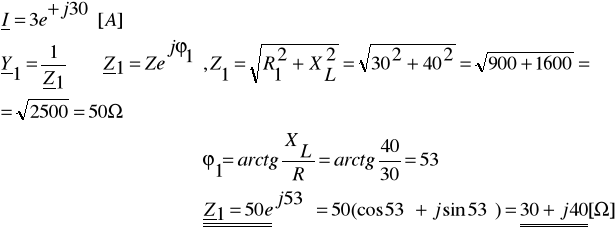
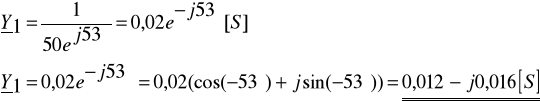
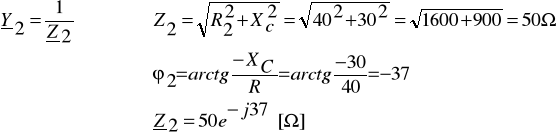
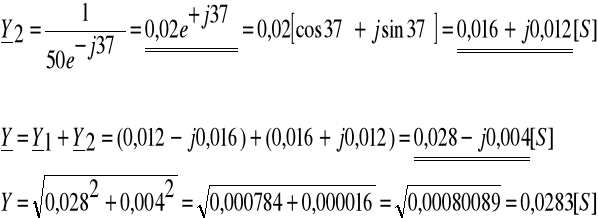
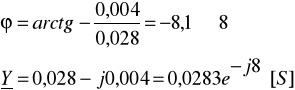
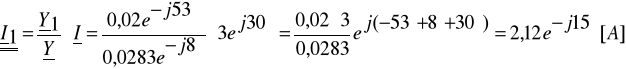
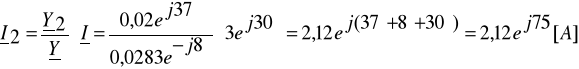
10. Obwody jednofazowe

Zadanie 1. Cewka o rezystancji R i indukcyjności L oraz kondensator o pojemności C połączono równolegle i zasilono napięciem u. Oblicz wartości symboliczne prądów I₁, I₂ i I, oraz wartości mocy zespolonych S₁, S₂ oraz S. Narysuj wykres wskazowy napięcia i prądów oraz wykresy trójkątowe: admitancji i mocy.

Dane:
, R = 50Ω, L = 0,1H, F = 50Hz, C =1 01,4μF.

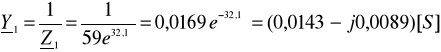
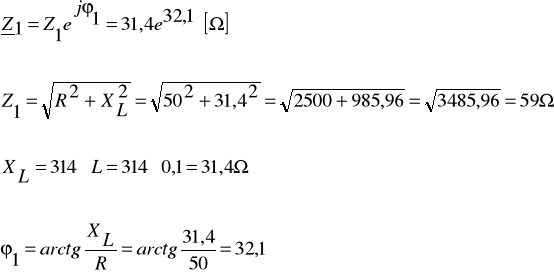
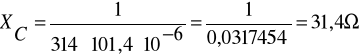
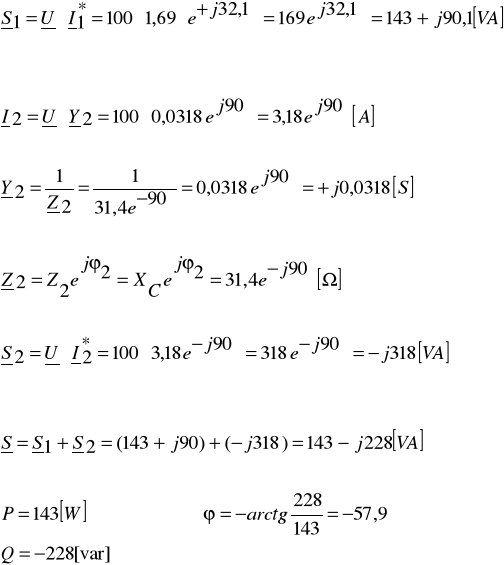
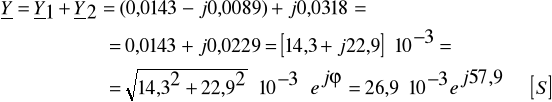
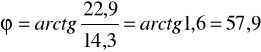
	Wykres wskazowy napięcia i prądów
	Wykres trójkątowy admitancji
	Wykres trójkątowy mocy

Zadanie 2. Cewkę o rezystancji R i indukcyjności L połączono równolegle z kondensatorem o takiej pojemności C, że występuje rezonans prądów. Oblicz wartość pojemności kondensatora C, wartości symboliczne prądów:I₁, I₂ i I oraz wartości mocy: S, P, Q₁ i Q_2. Narysuj wykres wskazowy napięcia i prądów oraz wykresy trójkątowe: admintancji i mocy.

Dane:
L = 0,1H, R = 50Ω, f = 50Hz.

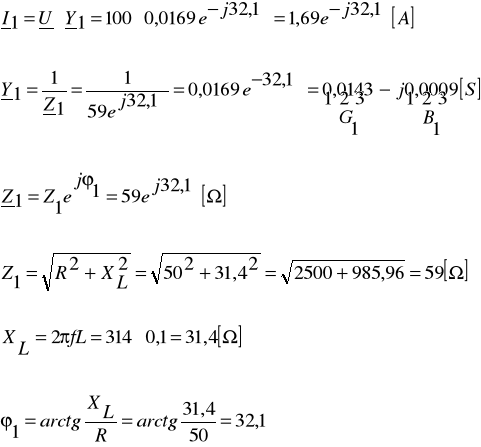
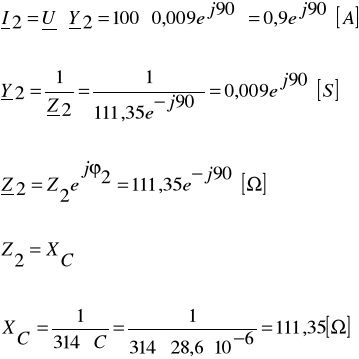
Warunek rezonansu prądu - susceptancja wypadkowa = 0

B=B₁+B₂=0

stąd B₁=-B₂

ale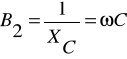

zatem

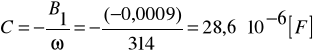
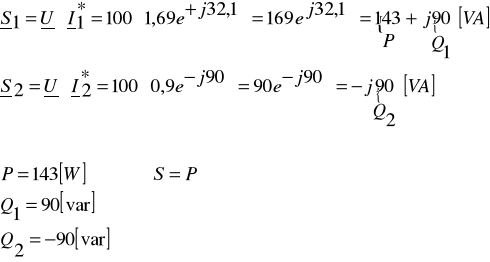
	Wykres wskazowy napięcia i prądów
	Wykres trójkątowy admitancji
	Wykres trójkątowy mocy

Zadanie 3

Cewkę o rezystancji R i indukcyjności L połączono szeregowo z kondensatorem o pojemności C. Obwód zasilono napięciem sinusoidalnym u(t). Kondensator ma taką wartość, że występuje rezonans napięć. Oblicz wartość C, wartość prądu I w obwodzie, wartości napięć U₁ na cewce i kondensatorze U₂ oraz wartości mocy: czynnej P, biernej Q i pozornej S, pobieranej przez dwójnik i przez jego elementy. Narysuj wykres prądu i napięć oraz wykresy trójkątowe impedancji i mocy.

Dane: R=50Ω

L=0,1H

f=50Hz

Rezonans napięcia jest to taki stan pracy obwodu elektrycznego, w którym reaktancja wypadkowa obwodu X jest równa zeru.

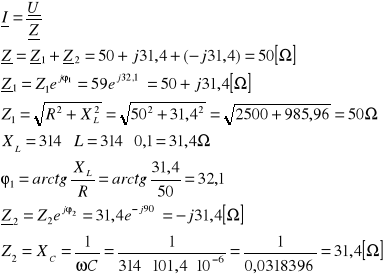
ale

czyli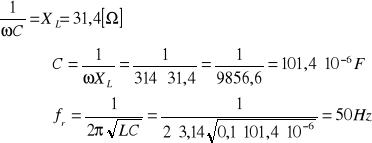

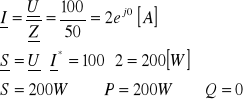
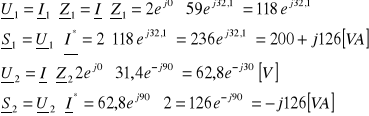
Zadanie 10.10

Określ wskazania przyrządów (I₁, I₂, I₃, U₁, U₂,P) w przedstawionym układzie odbiornika jednofazowego. Oblicz wartość mocy zespolonej (S) odbiornika oraz wartość mocy zespolonej gałęzi (S₁, S₂). Narysuj wykres wskazowy napięć (U₁, U₂, U) i prądów (I₁, I₂ i I₃ przyjmując I₁=I) oraz wykresy mocy (S₁, S₂, S₃ i S).

Dane:

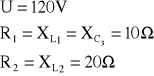
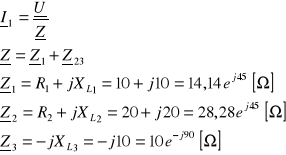
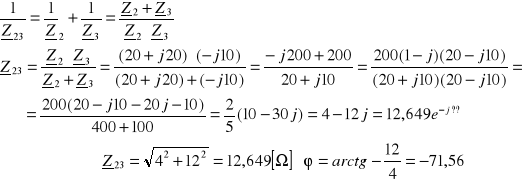
Zadanie 5

Oblicz rozpływ prądów (I₁₂, I₁₃, I₂₃, I₂₄, I₃₄) metodą przekształcenia obwodu w przedstawionym układzie odbiornika jednofazowego.

Dane:

Z₁₂ = 1 - j2 [Ω], Z₁₃ = 3 - j2 [Ω], Z₂₃ = 4 + j2 [Ω], Z₂₄ = 6 - j [Ω], Z₃₄ = 10 + j3 [Ω], U = 50 [V].

(
₁₂₃
Y₁₂₃):

Zamiana układu rezystorów liniowych trójkąt - gwiazda

(analogicznie impedancji oraz impedancji zespolonych)

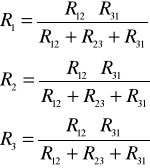
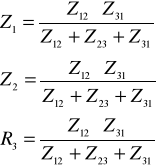
po zamianie (
₁₂₃
Y₁₂₃):

Obliczam impedancje po przekształceniu (
₁₂₃
Y₁₂₃):

,

,

,

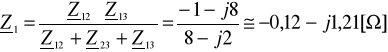
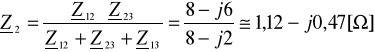
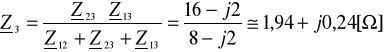
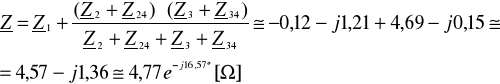
Obliczam prądy I, I₁₂, I₁₃, I₂₃, I₂₄, I₃₄

,

,

,

,

,

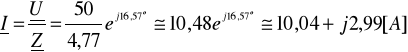
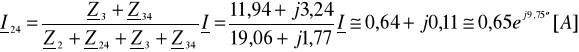
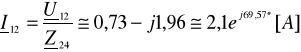
19

x=t/T

3

2

1

-2

-1

1

3/4

1/2

1/4

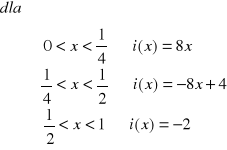
x=ωt

u(t)

100

100sinx

u(t)=100sinx

i(t)

u(x)

x=ωt

π

π

π

x=t/T

x_m

x`

0,5-x_m

0,5

1,0

1

)

0

100

π+α

u(t)=100sin

u(t)

x=ωt

α<π

2π

α

α

100

α

2π

U_L

π

100sinx

π

u(t)

x=ωt

I

U_L

U₂

A₃

φ

A₂

U

U_L

U_R

U

R

L

i

.

U_L

U_R

.

   

U

-30º

-60º

φ=30º

I

U_C

U_R

R

C

i

I

.

30º

-30º

U

U_C

.

U_R

U_L

U_R

R

L

i

C

U_C

I

φ=-49º

19º

-30º

   

U

(U_C - U_L

.

U_R

U_C

U_L

i₁

i₂

U

R

L

C

i

-30º

I₂

60º

19,1º

-30º

-60º

U

φ=10,9º

I₁

i₁

i₂

U

R₁

X₁

X₂

i

R₂

i₁

i₂

U

R₁

X_C

X_C

R₂

I₁

I₂

U

R

L

C

I

I

I₂

φ=90º

φ=57º,9º

U

φ₁=-32,1º

I₁

Y₂

Y

φ=90º

φ=57,9º

U

φ₁=-32,1º

Y₁

S₁

φ₁=32,1º

φ₂=-90º

φ=-57,9º

S

S₂

I₁

I₂

U

R

L

C

I

I₁

I₂

U

G₁

B₁

B₂

I

(B=B₁ +B₂=0)

U

G₁

I

S=P

-90º

φ=32,1º

S₂

S

Y₁

Y₂

φ₁

Y

I₁

I₂

φ₁

U

I

φ₂

U_L

U_R

R

L

I

C

U_C

U

U₁

φ₁=32,1º

U₂

U

φ₂=-90º

I

Z₁

Z₂

Z

S₁

S₂

S

W

A₁

R₁

L₁

I₂

I₃

V₂

A₃

A₂

U₂

R₂

C₃

L₂

V₁

U₁

U

I₁

cosx

π

x

A₁

W

I₂

I₃

C₃

L₂

I₁

R₂

U

V₂

R₁

L₁

V₁

Z₂₃

Z₁₃

Z₁₂

Z₃₄

Z₂₄

I₁₂

I₂₃

I

I₂₄

I₃₄

I₁₃

W

U

2

3

4

1

P

Z₄

Z₂₄

Z₃

Z₂

Z₁

U

I

U₁₂

Z₁ I

Z₂ I₂₄

Z₂₄I₂₄

Z₃I₃₄

Z₃₄I₃₄

1

1

3

2