004 3

6

Poziom energetyczny swobodnego elektronu jest dwukrotnie zdegenerowa-ny spinowo; jest to tzw. dublet Kramersa. Spinowe stany elektronu są opisane funkcjami spinowymi |a> i |/?> o różnych wartościach rzutu spinu na wybraną oś (tradycyjnie na oś z):

s‘» = l/2|oc>,    = -1/2 UJ>    (3.1)

Właśnie te dwa stany spinowe odgrywają zasadniczą rolę w opisie zjawiska EPR. Powstaje pytanie, jaka będzie energia stanów |a> i j/f>, jeśli elektron znajdzie się w stałym polu magnetycznym. Ze spinowym momentem pędu elektronu jest związany wektor (operator) momentu magnetycznego:

k =    (3.2)

gdzie: Ś oznacza operator (wektorowy) momentu spinu, g_B — magneton Bohra.

Współczynnik liczbowy g, nazywany czynnikiem rozszczepienia spektroskopowego, można obliczyć na podstawie elektrodynamiki kwantowej i jego wartość dla swobodnego elektronu wynosi 2,00232. Korzystając z mechaniki klasycznej możemy oddziaływanie momentu spinowego z polem magnetycznym zapisać operatorowo:

(3.3)

Wzór klasyczny na energię został zastąpiony wzorem operatorowym. We wzorze (3.3) znak kropki między wektorami oznacza ich iloczyn skalarny (ogólnie P-Q = P_xQ_x + P_yQ_y+ P_: Q_z). Ostateczna postać operatora, który będziemy nazywać hamiltonianem spinowym, jest następująca:

H, = _gfi_BBŚ.    (3.4)

W celu uproszczenia obliczeń, wybiera się układ współrzędnych tak, aby oś z była zgodna z kierunkiem indukcji pola magnetycznego. W tak wybranym układzie współrzędnych składowe pola magnetycznego B_x oraz B_y są równe zeru i hamiltonian (3.4) przyjmuje postać:

H, = gg»BŚ„ gdzie B s B,.    (3.5)

Działając tym operatorem na funkcje spinowe |a> i )/?> i korzystając ze wzorów (3.1) otrzymamy:

= 1/2 gg_BB\a,y,    = -1/2    (3-6)

Widać stąd, że funkcje |oc> i j/J> są również funkcjami własnymi operatora energii oddziaływania spinu elektronu z polem magnetycznym.

Wartości własne energii wynoszą:

^£a=l/2    E_p = -1(2 gn_BB_t    (3.7)

/

a więc różnica energii między poziomami [a) i |/ł> jest równa

=    (3.8)

Widzimy więc, że w polu magnetycznym następuje rozszczepienie poziomów energetycznych, co przedstawia rys. 3.1.

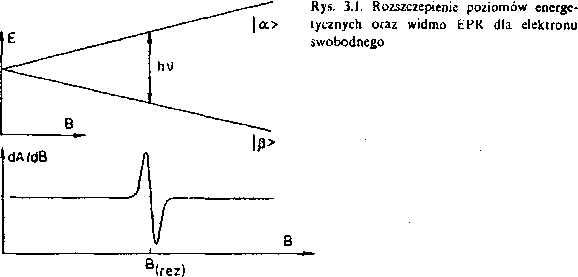
Jeśli elektron znajduje się również w polu elektromagnetycznym (wytworzonym przez klistron i falowodem doprowadzonym do rezonatora) o ustalonej energii kwantu hv, to warunek rezonansu {AE — /iv) ma postać

gti_BB = hv.    (3.9)

Warunek rezonansuj[3.9), dla stałej częstości promieniowania elektromagnetycznego v, jest^pełniony, jeśli indukcja magnetyczna osiąga wartość

£₍r«> - hv/gfi_B.    (3.10)

Aby odpowiedzieć na pytanie, czy rzeczywiście przy polu B_{(tz) wystąpi przejście między poziomami energetycznymi, należałoby obliczyć (na podstawie mechaniki kwantowej) prawdopodobieństwo przejścia między stanami |a) i |/f> pod wpływem pola elektromagnetycznego. Ogólnie z obliczeń takich wynika, że prawdopodobieństwo przejścia jest różne od zera, jeśli:

1)    kierunek promieniowania (lub jego składowej) jest prostopadły do kierunku stałego pola magnetycznego; jest to spełnione przez odpowiednią konstrukcję aparatu EPR;

2)    zmiana rzutu spinu na kierunek z-wynosi (zlSJ = U jest to tzw. reguła wyboru.

Przedstawione obliczenia dla elektronu swobodnego są dokładne, w miarę proste i wskazują metodę postępowania przy teoretycznym opisie zjawiska EPR. Hamiltonian spinowy dla rzeczywistych układów jest bardziej skomplikowany, co powoduje trudności w obliczeniu funkcji i wartości własnych hamiltonianu.