DFS

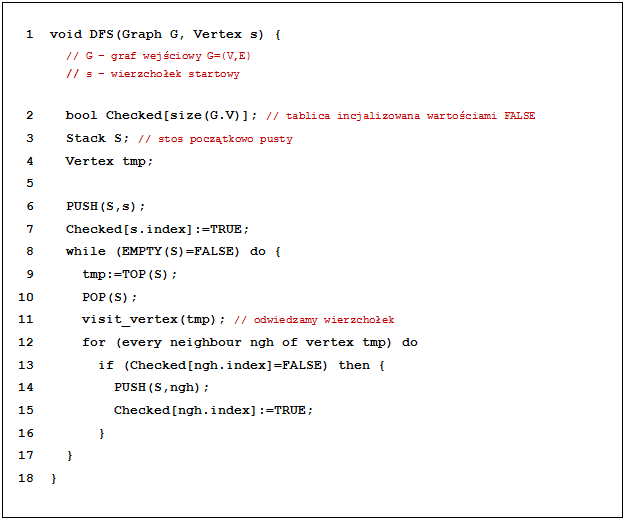
1    void DFS(Graph G, Vertex s) {

// G - graf wejściowy G=(V,E)

// s - wierzchołek startowy

2    bool Check.ed[size (G.V) ] ; // tablica incjalizowar.a wartościami FAL SE

3    Stack. S; //    stos    początkowo pusty

4    Vertex tmp;

5

6    PUSH(S,s);

7    Checked[s.index]:=TRUE;

8    while (EMPTY(S)=FALSE) do {

9    tmp:=TOP(S);

10    POP(S);

11    visit_vertex (tmp)    ;    //    odwiedzamy wierzchołek

12    for (every neighbour    ngh    of    vertex    tmp) do

13    if (Checked[ngh.index]=FALSE) then {

14    PUSH(S_fngh);

15    Checked[ngh.index]:=TRUE;

16    }

17    }

18    }