Image038

2.1.4. Szesnastkowy system liczbowy

Szesnastkowy system liczbowy jest to taki system pozycyjny, którego podstawa p — 2⁴. Do przedstawienia liczb w tym systemie potrzebnych jest 16 znaków. Dziesięć znaków stanowią cyfry arabskie, a pozostałe 6 znaków pierwsze litery alfabetu: A reprezentuje 10, B reprezentuje 11, F reprezentuje 15.

Liczba wyrażona w systemie szesnastkowym (N_lc) składająca się z ^-cyfrowej części całkowitej i m-cyfrowej części ułamkowej o postaci:

tyn— l&n-2    l#—2 •*• m]l6

gdzie a_t e {0,1,2, 3,4, 5, 6, 7, 8,9, A, B, C, Z>, £, F}, ma wartość:

Nie —    16"”¹+a_n_₂16^n_2-f ... +a₁16¹+a₀16° +

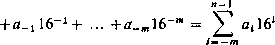
Kilka wybranych liczb szesnastkowych przedstawiono w czwartej kolumnie tablicy 2.2.

Niech liczba wyrażona w systemie szesnastkowym ma postać:

F3A, C8_l6

Równoważną jej liczbą dziesiętną jest liczba o postaci:

(15x 16²) + (3x 16¹) + (10x 16°) + (12x 16~¹) + (8x 16"²) = 4898,78125₁₀ Konwersji dziesiętno-szesnastkowej można dokonać na drodze wielokrotnego dzielenia na 16 części całkowitej oraz mnożenia przez 16 części ułamkowej przetwarzanej liczby dziesiętnej.

Przykład 1. Niech 2V₁₀ = 2527,78125₁₀ 2527:16 = 157 reszta 15₁₀ = F (LSD)

157:16 =    9    13₁₀ = D |

9:16-    0

9₁₀ = 9 (MSD)

2527₁₀ - 9DF₁₆

0,78125 x 16 = 12,5 = 0,5 nadmiar 12₁₀ = C (MSD)

0,5 x 16 = 8,0 = 0 nadmiar 8₁₀ = 8 (LSD)

0,78125₁₀ = C8₁₆

Wynik konwersji: 2527,78125₁₀ = 9£>F,C8_l6 Liczba przedstawiona w systemie dwójkowym może być bezpośrednio przetworzona na liczbę przedstawioną w systemie szesnastkowym. W tym celu należy liczbę dwójkową podzielić na grupy czterobitowe (tetrady) poczynając od przecinka w lewo i w prawo, i zastąpić otrzymane tetrady ekwiwalentnymi cyframi szesnastkowymi.

Przykład 2. Niech N₂ = 11010101000,1111010111

0110    1010    1000,    1111    0101    1100

6    A    | 8, F 5 C

MSD    LSD

Zatem 11010101000,1111010111₂ = 6/18,F5C_U

48