img034

34

3.4. Matematyczne aspekty procesu uczenia sieci

Wzór ten wygodnie będzie zapisać w postaci

q = Y,^Q(i)

gdzie oczywiście

Q⁰⁾ = \ (-^<J) - y⁽ⁱ⁾f

Ponieważ Q = Q(W), zatem poszukiwanie minimum może być dokonywane metodą gradientową. Skupiając uwagę na i-tej składowej wektora W, możemy więc zapisać:

XV: — Wi = Au?,- = — 11--

OWi

Wzór ten można interpretować w sposób następujący: poprawka Au;,- jakiej powinna podlegać i-ta składowa wektora W, musi być proporcjonalna do i-tej składowej gradientu funkcji Q. Znak - w omawianym wzorze wynika z faktu, że gradient Q wskazuje kierunek najszybszego wzrastania tej funkcji, podczas gdy w omawianej metodzie zależy nam na tym, by zmieniać W w kierunku najszybszego malenia blcdu popełnianego przez sieć, czyli w kierunku najszybszego malenia funkcji Q. Współczynnik proporcjonalności ij określa wielkość kroku Atu i może być w zasadzie wybierany dowolnie. W rzeczywistości jednak podlega on pewnym ograniczeniom. Przyjmując, że uczenie jest procesem stochastycznym (co znajduje uzasadnienie w stochastycznym charakterze ciągu uczącego U), możemy stwierdzić, że wartości r; powinny być zależne od numeru pokazu j, a zatem powinny tworzyć ciąg <    Uwzględniono to we wzorze wprowadzającym regułę uczenia, pisząc

zamiast ij. Z teorii aproksymacji stochastycznej można wyprowadzić wniosek, że powinny spełniać warunki

*)^U) - °°

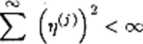
oraz

j=i

W najprostszym wypadku warunki te spełnia ciąg

ale szybkie malenie r/^ ze wzrostem j jest w tym wariancie czynnikiem zbyt silnie ogra-niczjącym efektywny czas uczenia (już dla niewielkich numerów j wartości stają się niniejsze od dokładności numerycznej używanego komputera i w kolejnych pokazach proces uczenia praktycznie zatrzymuje się, gdyż i/¹-'¹ = 0). Z tego względu, a także w celu ograniczenia'¹ wzrostu modułu wektora W, proponuje się niekiedy w charakterze ciągu r/U) wartości obliczane ze wzoru

¹Ogranicenie wzrostu modułu W jest celowe, ponieważ nieograniczcnic rosnące bezwzględne wartości składowych w, prowadzą do trudności z ich praktyczną realizacją zarówno przy symulacji komputerowej (pro-