img069

WIL gr. 7, 8,9 r. ak. 2010/11 Dynamika - przykłady zadań Ruch pod wpływem stałej siły

1. Ciało o masie m jest wciągane silą F na równię o kącie nachylenia a. Współczynnik tarcia wynosi p. a) Narysować wektory sil działających na klocek, b) Napisać wektorowe równanie ruchu oraz równania skalarne dla osi x i y. c) Wyznaczyć wartość siły F dla przypadku, gdy klocek porusza się ruchem jednostajnym.

2. Dane: masy Mj= 4kg, M₂ =lkg, kąt nachylenia równi a = 30°, współczynnik tarcia klocka o równię p=0.1, g=10m/s²

a)    Narysować wektory sil działających na klocki

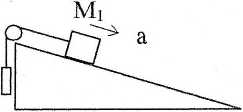
b)    Napisać wektorowe równanie ruchu (II zasadę dynamiki Newtona) oraz równania skalarne dla obu mas.

c)    Wyliczyć przyśpieszenie układu

d)    Wyliczyć wartość naprężenia nici.

M₂

Układ nieinercjalny

3.    Ciało o masie m spada swobodnie w windzie o wysokości h.

a)    Winda jest nieruchoma .

-    napisać II zasadę dynamiki Newtona dla ciała,

-    wy znaczyć czas t o spadku z wysokości h.

b)    Winda porusza się w dół z przyspieszeniem au=0.5 g.

-    napisać II zasadę dynamiki Newtona dla ciała,

-    wyznaczyć czas t spadku z wysokości h w ruchomej windzie.

c)    Winda porusza się w górę z przyspieszeniem a_u=0.5 g.

-    napisać II zasadę dynamiki Newtona dla ciała,

-    wyznaczyć czas t spadku z wysokości h w ruchomej windzie.

4.    Wahadło o masie m=0.2kg wisi swobodnie w poruszającym się wózku. Znaleźć kąt a nici z pionem oraz jej naprężenie N gdy:

a)    wózek porusza się z prędkością poziomą v = const

b)    wózek porusza się z przyspieszeniem poziomym a=5m/s²

Całkowanie równań ruchu.

Ruch pod wpływem sity zależnej od czasu.

5*. Punkt materialny o masie m porusza się wzdłuż osi x pod wpływem siły zgodnie z równaniem F(t)=A+Bt². Znaleźć zależność a(t), v(t), x(t) dla warunków początkowych: v(0)= 0, x(0)=0.

6*. Punkt materialny o masie m porusza się wzdłuż osi x pod wpływem siły zgodnie z równaniem F(t)=qEcosoi>t. Znaleźć zależność a(t), v(t), x(t) dla warunków początkowych; v(0)=0, x(0)=0.

Ruch pod wpływem sity zależnej-od prędkości

7*. Na samochód o masie m działa siła oporu F = -bmv . Prędkość początkowa samochodu v₀ (v₀,0). Znaleźć zależność prędkości i położenia samochodu w funkcji czasu. /r₀ = (0,0) /

8*. Cząstkę o masie m rzucono pionow'0 do góry (lub pionowo w dól) z prędkością początkową v₀ (0, v₀). Na cząstkę działa siła oporu F =-kv. Znaleźć zależność prędkości i położenia cząstki w^r funkcji czasu. ?₀ = (0,0).