MAT24

24

lim \A*)dx,

to granicę tę nazywamy całką niewłaściwą funkcji/w przedziale [a,b[ i oznaczamy ją symbolem

Podobnie określamy całkę niewłaściwą funkjci/określonej na przedziale ]a,b]. W takim przypadku,

= Jim jy(.x)rfx.

Przykłady

1.    Aby obliczyć całkę J zauważmy, że w tym przypadku jedynym punktem osobliwym funkcj

o

podcałkowej jest górna granica całkowania, tzn. +oo. Zatem, zgodnie z definicją,

+00    P

[ —= lim f —= lim Tarcta/- arctgOl =

J 1 + .x1    /»-+*> J 1 + X¹ P-^-^L    J 2

o    o

!

2.    W całce | funkcja podcałkowa ma jeden punkt osobliwy a = 0. Zatem,

7*

(" -&r = lim I" -4=- = lim^yT -2/o') = 2.

J /x e-o* j Vx a-O-k ^v /

Uwaga. Jeśli funkcja/ma dwa punkty osobliwe, jeden na początku, drugi na końcu przedziału ]o,ó[. to obieramy wewnątrz przedziału dowolny punkt c i obliczamy sumę całek niewłaściwych w przedziałach ]«,c] i [c,6[.

Przykłady

1. Funkcja wymierna | ma na prostej R tylko dwa punkty osobliwe a = -co i b = -fco. Dlatego też

-K»    O    +=0    O    P

dx

f_śk_₌ f_dx_ f_ijx__{= lim} f_rfx__{+ n} f _

j .X¹ + 4x + 9 j .x¹ + 4.x + 9 j .X¹ + 4.x + 9    J ,x¹ + 4.x + 9    P-™ i .x¹ + 4.x + 9

o

+ Hm -Ę-

Js J p~* 5

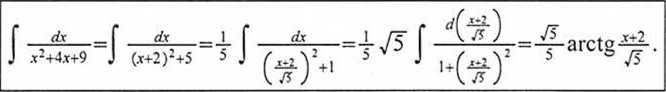
= lim -/P- ( arct- arctg ^u t/ I + Jim arctg-arctg

2_

^v&75

75

2

⁶ 75

TL

5

arctg—---
L 75	\ 2 J

75 J

₌ JL_n

5

1

Funkcja -- ¹ ma w przedziale ]0,1 [ dwa punkty osobliwe O i 1. Dlatego też

Opracował: Marian Malec