skanuj0001

30

lub

A £?JAJ^sin(^{tOt +} a*)⁼⁰ '    ^(2J0)

Ml,m> *-1

13 prawo Kirchhoffa - dla obwodów o napięciach i prądach zmiennych w czasie, zawierających rezystory, cewki i kondensatory - w celu uzyskania jednoznacznego sformułowania wymaga określenia dodatkowych założeń. Należy przyjąć, że obwód jest ekranowany od wpływu obcych strumieni elektrycznych i magnetycznych, a więc że nie indukują się dodatkowe ładunki w kondensatorach ani dodatkowe siły elektromotoryczne w cewkach (inaczej, że obwód nie jest sprzężony pojemnościowo i indukcyjnie z innymi obwodami). Ponadto zakłada się, że w stosunku do napięć występujących na cewkach złożonych z dużej liczby zwojów można pominąć siły elektromotoryczne indukcji własnej i wzajemnej indukowane w konturach oczek obwodu, będących pojedynczymi zwojami. Jeżeli spełnione są wymienione założenia, to II prawo Kirchhoffa dla napięć zmiennych w czasie przybiera postać:

A £V**=o,    (²¹¹>

ie{l,m) k-l

gdzie m jest liczbą wszystkich możliwych oczek (konturów) w obwodzie.

IW każdym zamkniętym konturze suma (po wszystkich gałęziach obwodu) napięć pomnożonych przez współczynniki i>_tt jest równa zero.

Współczynniki są zdefiniowane następująco:

(+1, gdy gałąź k ma orientację zgodną z orientacją oczka i,

-1, gdy gałąź k ma orientację przeciwną do orientacji oczka i,

0, gdy gałąź k nie należy do oczka i.

Przez orientację oczka rozumie się przyjęty kierunek obiegu. W rozważaniach nietopo-logicznych można orientację gałęzi opierać na napięciu. Przy rozważaniach topologicznych gałęzie są zorientowane prądami i należy pamiętać, że wszystkie gałęzie aktywne i pasywne mają napięcia zastrzałkowane przeciwko prądom.

Spośród wszystkich m możliwych do utworzenia oczek jest tylko n oczek niezależnych. Z rozważań topologicznych wynika, że

n -g-w* 1 .    (2.12)

Aby uniknąć sprzeczności w funkcjonowaniu II prawa Kirchhoffa, należy wykluczyć występowanie konturów złożonych wyłącznie z idealnych źródeł napięciowych.

Dla obwodów o wymuszeniach sinusoidalnych w stanie ustalonym każde napięcie w obwodzie ma postać u_k = | U_mh \ sin(cof + (3_k), więc II prawo Kirchhoffa przybiera postać:

A    (2.13)

2.3. Liniowe obwody elementarne przy wymuszeniu sinusoidalnym 2.3.1. Idealny rezystor

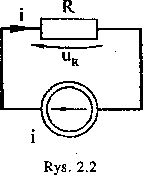
Idealny rezystor (rys. 2.2) jest to element bezinduk-cyjny i bezpojemnofciowy, dla którego pomija się zjawisko naskórkowości (skin effect ^!), czyli zakłada się R = const bez względu na wartość pulsacji to.

Dla dowolnych przebiegów związek między prądem i napięciem w rezystorze ma postać

u_R=Ri.    (2.14)

Dla prądowego wymuszenia sinusoidalnego

(2.15)

*' = |/Jsin(cor+t|0 ,    =

otrzymuje się

M_JJ=f?i=/?|/_m|sin(cot+ili)= li/^lśmlcot+ij;) , t|i_B = i|t ,    (2.16)

a więc dla rezystora przy sinusoidalnym wymuszeniu prądowym otrzymuje się odpowiedź napięciową'też sinusoidalną, przy czym amplituda napięcia

(2-12)

jest proporcjonalna do amplitudy prądu. Współczynnikiem proporcjonalności jest rezystancja R. Po podzieleniu równania (2.17) obustronnie przez -fi otrzymuje się związek dla wartości skutecznych

i^i    (2.i8)

a więc wartość skuteczna napięcia na rezystorze jest proporcjonalna przez współczynnik R do wartości skutecznej prądu płynącego przez rezystor. Jest to prawo Ohma dla wartości

) Zjawisko polega na wypieraniu prądu do zewnętrznych warstw przewodu. Prąd płynie mniejszym przekrojem. Uwidacznia się to jako zwiększenie się rezystancji wraz ze wzrostem pulsacji.