skanuj0008

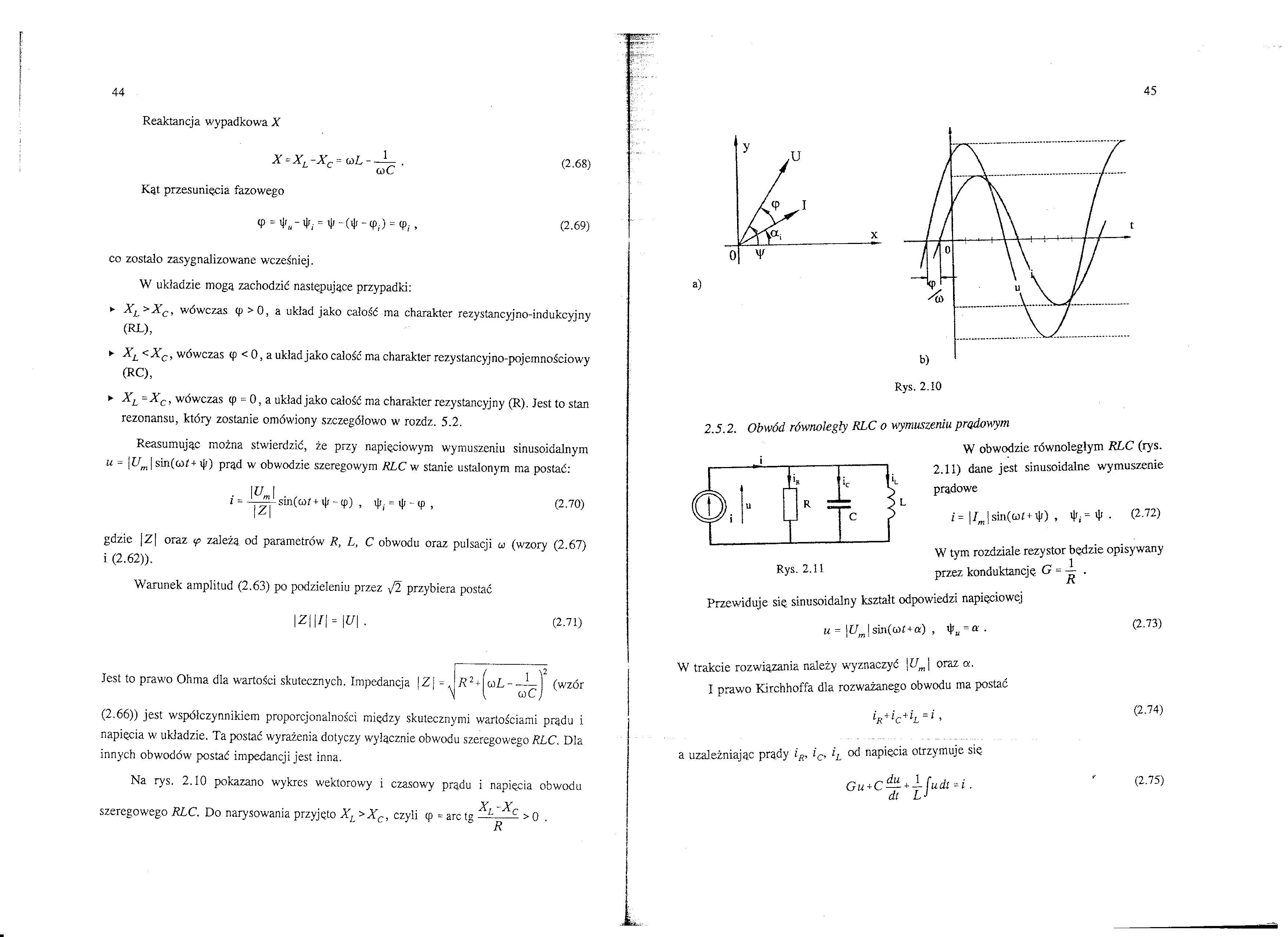
44

Reaktancja wypadkowa X

X - X_L ~X_C = coL- — .    (2.68)

G)C

Kąt przesunięcia fazowego

<P =='ł'-('l'-<P_;) = <P; >    (2-69)

co zostało zasygnalizowane wcześniej.

W układzie mogą zachodzić następujące przypadki:

►    X_L>X_C, wówczas tp >0, a układ jako całość ma charakter rezystancyjno-indukcyjny

(RL),

►    X_L < X_c, wówczas cp < 0, a układ jako całość ma charakter rezystancyjno-pojemnościowy (RC),

► X_L = X_c, wówczas tp = 0, a układ jako całość ma charakter rezystancyjny (R). Jest to stan rezonansu, który zostanie omówiony szczegółowo w rozdz. 5.2.

Reasumując można stwierdzić, że przy napięciowym wymuszeniu sinusoidalnym u = \U_m | sin(wt+ tj/) prąd w obwodzie szeregowym RLC w stanie ustalonym ma postać:

1 uj

\z\

sin(toi+1|/ - tp)

'I'/ = ł - <P

(2.70)

gdzie \Z\ oraz zależą od parametrów R, L, C obwodu oraz pulsacji co (wzory (2.67) i (2.62)).

Warunek amplitud (2.63) po podzieleniu przez -Jl przybiera postać

(2.71)

R² + \wL~ (wzór

coC

Jest to prawo Ohma dla wartości skutecznych. Impedancja \Z\

(2.66)) jest współczynnikiem proporcjonalności między skutecznymi wartościami prądu i napięcia w układzie. Ta postać wyrażenia dotyczy wyłącznie obwodu szeregowego RLC. Dla innych obwodów postać impedancji jest inna.

Na rys. 2.10 pokazano wykres wektorowy i czasowy prądu i napięcia obwodu

szeregowego RLC. Do narysowania przyjęto X_L>X_C, czyli tp = arctg

x_L-x_t

R

>0

b)

Rys. 2.10

2.5.2. Obwód równoległy RLC o wymuszeniu prądowym

i

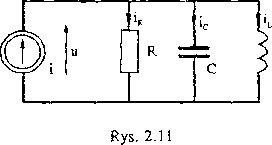
W obwodzie równoległym RLC (rys. 2.11) dane jest sinusoidalne wymuszenie prądowe

i= |/_m|sin(G)£ + t|r) , ty,. = t)i .    (2.72)

W tym rozdziale rezystor będzie opisywany

przez konduktancję G = -i .

K

Przewiduje się sinusoidalny kształt odpowiedzi napięciowej

u = jC/_OT|sin(tót+a) , rjr_u = et .    (2.73)

W trakcie rozwiązania należy wyznaczyć \U_m\ oraz a.

I prawo Kirchhoffa dla rozważanego obwodu ma postać

i_R + i_c+i_L=i,    (2-74)

a uzależniając prądy i_R, i_c, i_L od napięcia otrzymuje się

(2.75)

Gu+C — i- — fudt - i. dt LJ