skanuj0095

,_hli | I i-i: i-j li,,, I,li,. Uli NI 1,1 U nJ.U,U M ......................

190

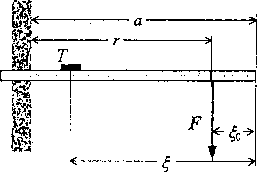
Rys.3. Schemat zamocowania płaskownika (2"- tensometr)

l*~ * —*	^Z1 1
—	....
tensometr)

Mocujemy teraz pręt w imadle - pod wpływem ciężaru własnego odkształca się i galwanometr wychyla się z położenia zerowego. Aby go doń z powrotem sprowadzić, należy przesunąć styk do położenia x\.

Teraz obciążamy pręt ciężarem F i ponownie notujemy położenie styku na drucie oporowym, przy którym mostek jest w równowadze.

Pomiary przeprowadzamy dla różnych długości ramienia r, na którym zawieszony jest ciężar i⁷.

Wyniki pomiarów wpisujemy do tabeli 1.

Tabela 1

k=....... E=....... Rs^=....... Ro ^=....... r_2E Rs _ k (R0+±R5)L
początkowe położenie styku x0 =......cm
r m	X i cm	Ax, - x,-x0 cm	cr N/m^2
obciążenie własne belki

Naprężenia obliczamy ze wzoru (8), w którym M₃ zastępujemy wyrażeniem (5). Wzór ten do obliczeń wygodnie jest przekształcić do postaci:

2M₃ E

r₃ T

1E_

k

*5

(R₀+$R_S)L

■ Ax = C • (x - x₀).

(9)

Wyniki obliczeń wpisujemy do tabeli 1.

Dla jednego pomiaru liczymy niepewność maksymalną a Sporządzamy wykres naprężenia w funkcji długości ramienia działania siły r, cr(r).

Zadanie 2 (dla studentów bardziej zaawansowanych)

Obliczyć wielkość naprężenia w tym samym miejscu zginanej belki, korzystając ze wzoru teorii sprężystości; porównać obliczoną wartość naprężenia z wartością uzyskaną z pomiaru.

Naprężenie belki dane jest wzorem:

M ■ z

gdzie: M jest momentem gnącym, tzn. sumą momentów sił zewnętrznych, działających na rozpatrywaną część belki, obliczoną względem środka ciężkości rozważanego przekroju, z - odległością rozpatrywanego punktu od osi obojętnej belki (u nas: z=h/2), J₀ - momentem bezwładności prostokątnego

ń-/i³

12

przekroju pręta względem poziomej osi symetrii: Ą = —— (rys.3).

Na moment gnący M składa się moment siły F: i moment własnego ciężaru belki Mi. Jeżeli długość belki (od zamocowania do swobodnego końca) oznaczamy przez a, a jej ciężar przez Q, to: