skanuj0099

j_:j j i; {i i|r i ................. IllUiul ................ii.......ii.WiUULiL.MI......

98

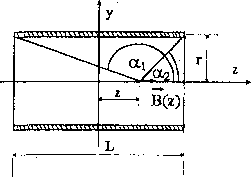
K ys.4. Schemat solenoidu wraz z oznaczeniami stosowanymi we wzorze (3)

Znając parametry geometryczne solenoidu oraz natężenie płynącego przezeń prądu I_s można stosunkowo łatwo obliczyć indukcję pola magnetycznego dla punktów leżących na jego osi, korzystając z prawa Biota-Savarta, co prowadzi do wzoru:

B,

JU₀I,N cosa₂-cosa_t

(3)

-{LI 2+z)

h =-7==== , 4r^{1 2}+{L/2 + zf

{LI 2-z)

Vr² + {L/2-z)² ’

(4)

- >*,<ninic z oznaczeniami według rys.4. Dla z= 0 (środek solenoidu) otrzymujemy:

(5)

ł. Wykonanie ćwiczenia

'

/ u il n u i e 1    ;

W yznaczyć zależność napięcia Halla od natężenia prądu zasilającego hallo- i Inni ! i'_n -f{I) w stałym polu magnetycznym.

2. Pomiary wykonać dla ok. 10 różnych natężeń Ih prądu zasilającego hallo-tron. Dla każdej wartości I_H odczytać najpierw napięcie asymetrii U_R (przy wyłączonym polu magnetycznym), a następnie włączyć na chwilę prąd zasilający solenoid i odczytać na woltomierzu cyfrowym napięcie U. Jako napięcie Halla U_H przyjąć różnicę U-U_R- Wyniki ująć w tabeli 2.

Tabela 2

Lp.	Ih mA	Ur mV	U mV	UH^U-UR mV

Zadanie 2

Wyznaczyć zależność napięcia Halla od natężenia prądu zasilającego solenoid U_H ~f(I_s )■

1.    Ustawić wartość natężenia prądu In zasilającego hallotron na stałą wartość /o podaną przez prowadzącego ćwiczenie. Dla I_s = 0 odczytać na woltomierzu napięcie asymetrii Ur .

2.    Wyznaczyć napięcie Halla dla ok. 10 wartości I_s. Wyniki ująć w tabeli 3.

Tabela 3

7o = ...			Ur0 -...
Lp.	Is A	U mV		U» - U-Ur0 mV

1

i (mieścić hallotron w geometrycznym środku solenoidu. Wartość natężenia

2

|'ii|iln I_:( zasilającego solenoid ustawić na stałą wartość I_s0 podaną przez prowadzi)! i'f',0 ćwiczenie.