skanuj0115

odległości od środka przekroju poprzecznego, ani też zasady ich prostopadłości do promienia, jak przy skręcaniu prętów o przekroju kołowym.

W przypadku skręcania pręta o przekroju prostokątnym wykazuje się, że:

—    naprężenia tnące w narożach są równe zeru,

—    naprężenia tnące w punktach położonych przy konturze przekroju poprzecznego są styczne do zarysu, to jest skierowane wzdłuż boków prostokąta,

—    największe naprężenia styczne i„„ występują w środku dłuższych boków prostokąta.

Wartość naprężeń r_m>„ powstających w pręcie o przekroju prostokątnym skręcanym momentem oblicza się ze wzoru podanego przez Saint-Yenanta:

aab²

MPa.

(8.17)

We wzorze tym a i b oznaczają długości boków przekroju poprzecznego pręta skręcanego (rys. 8.10), a a jest współczynnikiem, którego wartość zależna jest od stosunku a/b.

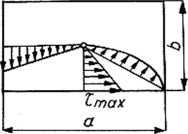
Rys. 8.10

Jednostkowy kąt skręcenia pręta (to jest kąt, o jaki obrócą się względem siebie dwa przekroje poprzeczne oddalone o jednostkę długości) oblicza się ze wzoru:

0 =

M,

Jab^G

rad,

(8.18)

w którym C jest modułem sprężystości postaciowej, a p - współczynnikiem zależnym od stosunku ajh.

Wartości współczynników a i /? podano w (abl. 8.2.

Tablica S.2

a/b	1	1,5	2	2,5	3	4	5	6	8	10	00
a	0,208	0,231	0,246	0,258	0,267	0,282	0,293	0,299	0307	0313	0,333
p	0,141	0,196	0,229	0,249	0,263	0,281	0,293	0,299	0J07	0313	0333

138