zadania 2

|
Okresy |
Rn |
R2t |
Rit-E(Ri) |
R2t-E(R2) |
[Rn-EjR,)]2 |
[R21-E(R2)f |
[Rn-E(R,)] * [R2t -E(R2)] |
|
1 |
10 |
9 | |||||
|
2 |
9 |
9 | |||||
|
3 |
10 |
7 | |||||
|
4 |
7 |
10 | |||||
|
5 |
2 |
3 | |||||
|
6 |
3 |
6 | |||||
|
7 |
4 |
4 | |||||
|
8 |
2 |
0 | |||||
|
9 |
3 |
2 | |||||
|
10 |
4 |
1 | |||||
|
Razem |
54 |
51 |
X |
X |
t fa-RjRn-Ri)
r'2 = " Mfcs,
n - liczba okresów z przeszłości, z których pochodzą informacje,
R,- stopa zysku papieru wartościowego osiągnięta w t - tym okresie,
Ru- stopa zysku pierwszej akcji osiągnięta w t - tym okresie,
R2t - stopa zysku drugiej akcji osiągnięta w t - tym okresie,
R,- oczekiwana stopa zysku pierwszej akcji,
R2- oczekiwana stopa zysku drugiej akcji,
S| - odchylenie standardowe pierwszej akcji,
S2 - odchylenie standardowe drugiej akcji,
Zad. 4
W skład portfela inwestora wchodzi 15 akcji firmy A po 10 zł i 25 akcji firmy B po 8 zł. Wyznacz stopę zysku oraz ryzyko dwuskładnikowego portfela, mając następujące dane:
1. Stopy zysku dwóch akcji - 9% i 11%,
2. Ryzyko poszczególnych akcji - 2,7% i 1,5%,
3. Współczynnik korelacji - 0,45.
£(/?p)=C/1£(i?,)+f/2£(Ą)
S, +U22S22 +2 U,U2S,Ssn
Ui - udział wartościowy pierwszej akcji w portfelu,
U2-udział wartościowy drugiej akcji w portfelu,
Zad. 5
Rozpatrywane są dwie akcje A i B. Ryzyko związane z akcją A wynosi 9%, a z akcją B 11%. Powiązanie stóp zysku tych dwóch akcji - mierzone współczynnikiem korelacji - wynosi 0,63. Dla jakich udziałów akcji w portfelu posiadacz tych akcji osiągnie minimalną wartość ryzyka i ile ono wynosi?
S22-S,S2rn
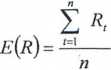
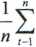
n-1
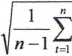
Wyszukiwarka
Podobne podstrony:
Prąd Zmienny Zadanie (4) i mtfczyc i rn pedancie zastępczy. jeże ii: l<; « 30
13759 wzmacniacze04 WZMACNIACZ TRANZYSTOROWY W UKŁADZIE OB T Tl - BC 107 Ri- 820 R2- 10 k
skanuj0015 Ćwiczenie-1 [1]. Dane są: Ei =20V; E3=5V; Ri=lD; R2=3Q; R3=2O; E R4=l£2; Rs=4fl Oblic
Wzmacniacz do pods?uchu ok 1km Spis elementów Symbol Wartość RI 68k R2 100Q R3 100Q R4 6,8k lu
K> Df ĆN i# Q rit n o >4 ri 0 9tł ° 4 4H 9+ ^ CO OI ® p 8 a ® 94, U< z
zadania (4) t,) u.■tv.(*«-*- > -Ł>łn -Ł^(«.-i»)- ■5&ri s) 6<x ^
Zadanie 7 Dwa dane okręgi o środkach O, i 02, i promieniach i R2, połączyć dwiema stycznymi położony
Wyznacz (np. metodą superpozycji) wartość natężenia prądu płynącego przez rezystancję R3 h Ri=1Q R2=
kolokwium 3 2 Zadanie 3. Proszę obliczyć granice następujących funkcji: lim (/.r2 + x - 1 — Jx2 — x
DSC00460 3. Oblicz za pomoq pran» KirdłfcttfTa f rarf i 11 a) Gdzie: E=12V. RI-4k11 R2 1tt£L ŁV»IM:
zadanie s2 (2) 7 > r OJ ^ » *© 5/tlUr; Pi ^ f 4 ri W&g) > ^ ć Jd T 0% =
więcej podobnych podstron