Zdj 25252525EAcie041

Ćwiczenie laboratoryjne Nr H

K()/\\l\/\\\ \MI KOWWŃH KI \IK>\\ l«(W NĄ.N KO/.MI /M_)_\V

icvi wicie metod numerycznych du/ących do rozwiązywania równań różniczkowy tli Najbaidz /tunc to mekda Eulera. Kungego Kulty (u %knkii rk).

MjiłKAi poo*da gotowe procedury służące do poszukiwaniu rozwiązania równania rózmczkow Każda / nich podaje wynik w postaci macierzy o rozmiarze zalc/nyrn od rzędu rozwiązywanej: •

\ I nx\\it c RunprgpKutty oporic są procedury rkfi\c<! oraz Kkmhipt Procedura rkfmd u/

¹:okrcku cali owama , tutomusi procedura Kkadapt w procesie rozwiązywan a sprawdza błąd lokalny rozwiązania i w razie potrzeby zmienia kmk całkowania.

Składnia procedur jc*J następująca

J-= rkfi\t*h Y.tl.L2Jp.D) oraz /:-Rkadapl(Y.t I .t2Jp.D) gdzie

>    - wektur zaw ierający wartości początkowe.

11.12 - ki*icc prwdruhi rrairwcfu w którym wyznaczone zostaną wartości funkcji niewiadomi !p - liczba punktem dla których znajdujemy wartości funkcji niew iadomej.

[>t.Y> - wektor zawierający pochodne szukanych funkcji

Do rozwiązywania równań nłttścadkoeydi nkltiuow >vh można u/yć błiku given - odcsols i Składnia instrukcji odtwoltc jot następująca

>    eodc«olveuji)

» rrwenn* mczalr/na n - cn.’jdm punkt ;*rzrdziafu <t)M>

«K/rnir I.

V />,iz r.mnamc i ♦ 41 *0 w przedziale <tl.l>i warunkiem początkowym y(0) • 3

Ja>    lxi.y> :•-4 )u

/ - rkfitrdy.fi. 1.100.Dl

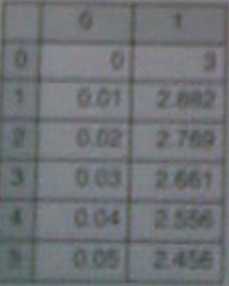
Ri^ucuu0 uąter?) / zawierz ctu, k-rtfamna I t/ckaną fufticyę ytt) W %im rjdrzix'*n i:Jvo :ł y    czat u