0000020 2

12 3 4

1    2    2    10

P(C) -

2    2    0    0    0

3    0    0    0    0

4    0    0    0    0.

Olo hipergrafu aecierz przejść jost określono w analogiczny sposób.

Nleklody wystarczy posługiwanie się binornę eaciorzę • przejść

gdzie

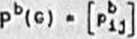
O . fldy p_AJ - O

^{1 sdy P}ij ^{> 0}

• • • • #

1 gdy V x ■ ^i.«.«x.)...i. <x,u>eP    ¹ J

O w przeciwnym przypadku

Macierze praojść sę wykorzystywano głównie przy rozwiązywaniu problemów polegajęcych na wyznaczoniu odpowiednich dróg w gre-foch.

2.3. Charakterystyki wierzchołków grefu

waśniony pod uwagę dowolny graf C • <X, U. P> . Określa się noetępujęce, liczbowo charakterystyki jego wierzchołków: Stapiać wierzchołka o(x); x€X

s(x) • e*(x) ♦ e“(x) » e~(x) ♦ s°(x)

gdzie

o*(x) - stopień zewnętrzny wierzchołka

x - ilość łuków “wychodzęcych* z wierzchołka xr

„♦(X) ■    « _yy_x [y * XA<x.y.u>£P]}| ,

o“(x) - a t o p i a ń wewnętrzny wiorzchołko x - lloóć łuków “wchodzących” do wierzchołka x :

o‘(x) - |{ u fcU : _yV, [y / xA<y.x,u>6p]}| ;

a“'(x) - lloóć krowędzi incydontnych z wierzchołkloc x i

e-(x) - 11 u fc U « V_x[y ¥ xA<x.y,u>£PA<y,x.u £p]}| ;

•°(x) - lloóć pętli incydontnych z wiorzchołkioa x j

a°(x) - |(u6U :<x,x,u>€P}|.

Stopień grafu

S(G) ■ wax a(x) x€ X

Stopień BlnlBolny grafu

SJC) • min o(x)

⁰ x£X

Rozwidlonio wierzchołka r(x); x£Xi r(x) - o *(x) ♦ a“(x) ♦ e”(x) ♦ 2»o°(x)

^C2yl1    r(x) ■ o(x) ♦ c°(x)

Rozwidlania grafu

R(G) • nex r(x) x€X

Rozwidlonio ■inieolne grofu

R (G) ■ oin r(x)

⁰    *c X

Zalotnie od wartoóci e(x) 1 r(x) wyróżniamy:

39