093(1)

/'(*) = -1-

~~r 'g^e> /"(*) = 73 >gc

«V    -V

zatem/'(x) < O i/"(x) > O w całym przedziale [1,6; 1,8].

Przekonawszy się, że funkcja/(x) ma różne znaki na końcach przedziału i że pochodne f'(x) i f"(x) zachowują w tym przedziale swe znaki, oznaczamy końce przedziału: a = 1,6 = fi, b = 1,8 i stosujemy wzory uściślające (*); mamy

(1,8 — 1,6)/(1,6)

cii = 1,6-

/(1,8)-/(1,6)

/(1,6)

- 1,6+0,1559 = 1,7559

f^ = 1,6+0,1540

1,7540

Stosujemy ponownie wzory (*) do otrzymanego nowego przedziału, dotąd, aż jego długość stanie się mniejsza od wielkości podwojonego błędu przyjętego w warunkach zadania, czyli mniejsza od 0,000 002. Znajdujemy

a₂ = 1,7559

(1,7540 —1,7559)/(1,7559)

b₂ = 1,7540

/(l,7540)-/(l,7559) /(1,7540)

1,755 58

= 1,755 57

/'(1,7540)

a₃ = 1,755 5816,    b_}= 1,755 580 7

Od liczby 0,000 002 mniejsza jest długość przedziału [+. n₃], ponieważ a₂—b_} — 0,000 000 9. Dlatego szukana przybliżona wartość pierwiastka danego równania, obliczana z dokładnością do 0,000 001, wynosi

x₀

2

1,755 581

W zad. 410—413 wyznaczyć ilość pierwiastków rzeczywistych równania i obliczyć największy z nich z dokładnością do 0,01:

410. x³-9x-5 = 0    411. x⁴—x—10 - 0

412. x—sin2x = 0    413. x-2+e* = 0

W zad. 414—417 obliczyć przybliżone wartośći pierwiastków rzeczywistych równania z dokładnością do 0,01:

414. x³—6x+3 = 0    415. x⁴+10x-100 = 0

416. (x—l)²—2sinx = 0    417. e*-2(l-x)² = 0

§ 11. Krzywizna krzywej płaskiej

Jeżeli linia jest określona w prostokątnym układzie współrzędnych za pomocą równań y = f(x) lub F(x, y) = 0, lub parametrycznie x = — <7>(0, y — V(0, ^to j^ej krzywizna K w dowolnym punkcie jest określona wzorem

(1)

K =

1/1    \xy-yx\

[i+(/)T    (*²+./)²

przy czym x, x, y, y oznaczają pierwsze i drugie pochodne x i y względem parametru t.

Krzywizna linii w pewnym jej punkcie charakteryzuje odchylenie linii od stycznej do niej w tym punkcie.

Spośród wszystkich krzywych płaskich stałą krzywiznę mają jedynie okrąg i linia prosta. Dla innych linii krzywizna zmienia się wraz z położeniem punktu. Krzywizna prostej jest wszędzie równa zeru; dla innych linii może to zachodzić tylko w pojedynczych punktach. Krzywizna okręgu

o promieniu R jest w każdym jego punkcie równa

Wielkość R — będąca odwrotnością krzywizny w pewnym punkcie

A.

krzywej, nazywamy promieniem krzywizny krzywej w tym punkcie.

Kołem krzywizny krzywej w punkcie M tej krzywej nazywamy okrąg o promieniu równym promieniowi krzywizny w punkcie M i o środku C leżącym na normalnej do krzywej po stronie jej wklęsłości (rys. 87).

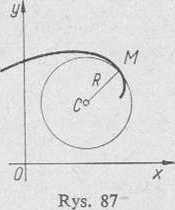
Współrzędne (A', Y) środka krzywizny krzywej (środka koła krzywizny) w punkcie M(x, y) krzywej określone są wzorami

*²+/    „ i + (y')\.

X = x-

y+

xy—yx

x²+y²

y = x-

xy—yx

A+

/' ' i+O')²

(2)

189