100 41

90

ekstremalne o faz określmy, jakim płaszczyznom są one przyporządkowane. Poszukiwanie takiego układu współrzędnych (czytaj: płaszczyzn, którymi przecinamy bryłę), w którym określona macierz przyjmuje ekstremalne wartości elementów na diagonalnej (czytaj: ekstremalne naprężenia normalne) znane jest w rachunku tensorowym, jako szukanie wektorów własnych i wartości własnych. Rozwiązanie tego zadania sprowadza się do znale* zicnia takich wektorów i takich liczb cr_(f), aby

2V»^W — <T|»^W (nie ma sumowania względem i) .

Znalezienie więc ekstremalnych naprężeń normalnych oraz odpowiednich płaszczyzn przekroją sprowadza się do wykorzystania formalnych reguł rachunku tensorowego przy wyznaczaniu wartości i wektorów własnych. Dodajmy, że ekstremalne naprężenia nor* malne nazywać będziemy naprężeniami głównymi, zaś przyporządkowane im płaszczyzny — płaszczyznami głównymi.

Ze względu na praktyczne znaczenie toku postępowania przy wyznaczaniu wartości własnych (naprężeń Równych) oraz wektorów własnych (płaszczyzn głównych) powtórzymy odpowiedni rozdział rachunku tensorowego na przykładzie tensora naprężeń.

Jak widać ze wzoru (3.21) <r_u jest funkcją trzech zmiennych (a_a, a_ł2, a_i3), które jednakże nie są zmiennymi niezależnymi, wiąże je bowiem warunek

(3.22)

Rozpisując warunek konieczny istnienia ekstremum funkcji (3.21) z warunkiem pobocz-

nym (3.22) i przyjmując oznaczenie „—a₍₀” dla mnożnika Lagrange’a, otrzymujemy następujący układ równań algebraicznych:

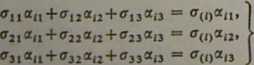
(po prawej stronie nie ma sumowania względem i), które wraz z równaniem (3.22) pozwolą na znalezienie oraz a_tJ (j = 1,2,3). Zanim przystąpimy do rozwiązania tego układu zwróćmy uwagę, że równania (3.23) możemy zapisać w postaci

lub krótko:

(3.24)

7V*^(t) — <r₍₀e⁽⁰ (nie ma sumowania względem f). Jeśli układ (3.23) zapiszemy w postaci

(3.25)

n

to zauważamy — że jest to układ jednorodny ze względu na szukane *,/ (/    1,2, 3>,

a zatem niezerowe rozwiązanie istnieje wtedy, gdy wyznacznik macierzy utworzony ze współczynników przy niewiadomych jest równy zeru, czyli

^orn'"'0(i/»    *i*

^11*    I “ 0.    02^

°^r33^-~^<ycn|

Wynika to z następującego rozumowania. Oznaczmy: «(<?,e₁₇, <? _j;, ó(<r₂j,<r_2a-«r₍₀, <r₂₃), c(a₃₁, <r₃₂, er₃₃-<7₍₀), X(x_n,a_n,a_n); wówczas równania (3.25) zapiszemy «*Af ■ O, b‘‘X — O, c-AT = 0. Szukaną wielkością jest X ^ 0. Iloczyny skalarne wskazują, że X powinien być prostopadły do wszystkich trzech wektorów u, b, e. 7—u^, nie takiego wektora AT jest możliwe wtedy, jeśli a, bic leżą w jednej płaszczyźnie (rys. 3.10).

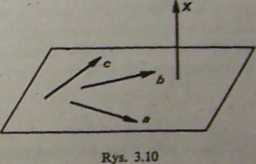
Warunkiem komplanaraości tych wektorów jest zerowanie się iloczynu mieszanego c] = 0. Warunek ten zapisany za pomocą współrzędnych ma postać (3.26). Jefi zapewnimy komplanamość wektorów c, b, c, to poszukując wektora AT wystarczy zapewnić jego prostopadłość tylko do dwóch wektorów z trójki s, b_p c, oczywiście do takich dwóch, które nie są równolegle. Inaczej mówiąc, jeśli spełnimy dwa równania (3.25), trwać spełnione automatycznie.

Zerowanie się wyznacznika (326) zapewniamy dobierając odpowiednie <r_w. Rozpisany wyznacznik daje równanie

<r*Q—* 0*    (3-27)

gdzie

J_t ■ ffii+^ai+^nt