Ciąg poligonowy otwarty obustronnie nawiązany Teoria

Ciąg poligonowy otwarty obustronnie nawiązany.

Teoria.

iv:    A'

©-'*--M^)

..-A

łUWWAJik. oV>WlO.V\( OJ

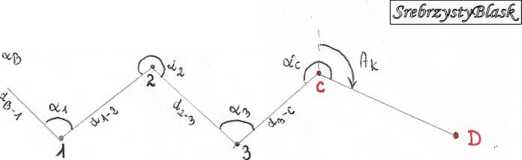
Ciąg poligonowy otwarty z pełnym nawiązaniem obustronnym posiada z każdej strony 2 elementy nawiązania: kąt i bok, którymi jest geometrycznie połączony z punktami osnowy wyższej klasy łub rzędu. Kolejność obliczeń:

1.    Na podstawie dzienników pomiarowych, szkicu osnowy i wykazu współrzędnych wpisujemy do formularza obliczeniowego dane liczbowe.

2.    Obliczenie azymutów' boków kierunkowych: Ap= A.\b i A₍;_D

3.    Obliczenie sumy praktycznej kątów lewych lub prawych:    ^ i [jb]r>

4.    Obliczenie sumy teoretycznej katów' lewych lub prawy ch Dla kątów lewych iX]t ⁼ A- A ⁴ ^(.200 “i)

Dla kątów prawy ch j>l_t- Pf - A ⁴ X) JiO'³

5.    Obliczenie odchyłki kątowej fk_t otrzy manej jako różnica sumy praktycznej i teoretycznej katów ciągu

^a tój - LAt    - ll^At

6.    Obliczenie odchyłki kątowej dopuszczalnej fkt max i porównanie z nią odchyłki otrzymanej

fkt- ^    twWyy" - W₀ [v.

Ata/    O    pOtYj-ij X tlW^Yi —

do    -

bU>|d) /yudnw    Mj

7.    Rozrzucenie równomiernie otrzymanej odchyłki kątowej na poszczególne kąty

8.    Obliczenie azymutów boków na podstawie wartości azymutu początkowego początkowego poprawionych kątów. Kontrolą obliczenia jest uzyskanie na końcu rachunku niezmienionego azymutu końcowego.

9.    Obliczenie przyrostów współrzędnych A X i AY poszczególnych boków.

10.    Kontrola obliczeń przyrostów.

11.    Obliczenie sum praktycznych praktycznych teoretycznych przyrostów

t>x3p    [a*V->VV_? AAtr- AA?

i fi

i 60" ($o^ŁŁ) *u> = i 'bo" UoA

V*jt

. _ Ji£

12.    Obliczenie odchyłek przyrostów

1* - Cax3 p - La At

?_r

13.    Porównanie odchyłki f [ z odchyłką f l

JWX%

W

fUflr

ii.

fl

PiYYjy

4.0

i,?

2.0

\G W 4,0 M 5

o,i

0,3)

OM

m

o.te Ofof Of)t 0,60

14.    Rozrzucenie odchyłek przyrostów proporcjonalnie do długości boków

V -X- - I* , - \i -N _ —    -    i,'- koWmu lA-

^ A ' w (,    ^    L A    s _A - 9, j

^    L' Aa. .

15.    Obliczenie współrzędnych punktów na podstawie współrzędnych poprzednich i poprawionych przyrostów.

’Xn    AY-ęw