DSCN1825

90

Pmtirttnm uiM liI

IR. II

| 9. Środek ciężkości

286. Wyznaczyć położenie środka ciężkości (7 ramki AFBD Ujadającej sio * luku ADB bodącego ćwiartką okręgu koła o promieniu FD—R i półokręgu AFB zbudowanego na oięolwie AB jako średnicy. Ciężar jednostki długości obu prętów tworzących ramkę jest jednakowy.

AD

Odp.    + —13-2^3)«0,524 B.

A

Rys. do ni ttt

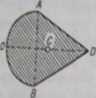
Rys. do ud. 287.

i*0

In. do ud. ttt.

287.    Wyznaczyć położenie środka ciężkości C powierzchni ograniczonej półotręgicm AOB o promieniu R i dwiema prostymi równej długości AD i DB, jeśli 0£-3£.

^oc“ffS^s=i-^i9j?-

288.    Znaleźć środek ciężkości powierzchni odcinka koła ADB o promieniu A0=30 cm, jeżeli kąt A0£«6O*.

Odp. OC-2J7 cm.

289. Wyznaczyć położenie środka ciężkości O jednorodnego krążka z okrągłym otworem zakładając, że promień krążka wynosi r„ promień otwo-ro r_M a jego środek znajduje

się w odległości y od środka krążka.    .

^94pv^i*fe

290. Znaleźć współrzędne środka ciężkości przekroju poprzecznego kątownika nietównortmłennego, którego półki mają szerokość 0A*o, 0£-6, a grubość AO—BD—d.

^0dp' '"jta+ł^ń’ ^s"2(h«-«)'

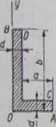
Rys. do ud. 200.

rru .■

19]

drodeJc tKiłsfci

91

291. Zńnlośó odległość środka ciężkości przekroju teownika ABCD od jego boku AO, jeżeli wysokość środnika DB*h, szerokość pÓUd i(7-e, grubość półki wynosi i, a grubość środnika ś.

Odp.

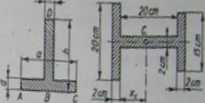
2(*d+tt~M)

292.    Znaleźć środek ciężkości profilu dwuteowego, którego wymiary podano na rysunku.

Odp. z₀=*9cm.

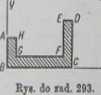
293.    Zoaleśó współrzędne Rys. do ad. Ml. •lyz. do ud. żtt. środka ciężkości jednorodnej

płytki przedstawionej na rysunku wiedząc, że Aff=2cm, £0-1,1 em, AB-J cm, £C=10 cm, £F-Ś cm, RDm2 cm.

_ 10 10

Odp. *o-5—ca, y₀=l~ ca.

W    19

294.    W jednorodnej kwadratowej płycie ABCD o boku A£-lm wydęto kwadratowy otwór BFOH, którego boki są odpowiednio równo-legie do boków płyty ABCD i wynoszą 0,7 m każdy. Obliczyć współrzędne 41 środka ciężkości pozostałej częśd płyty wiedząc, «• 01--0,jr-O,5 m, gdzie O i 0, są środkami kwadratów, przy czym odcinki OK i O_xK są odpowiednio równoległe do boków kwadratów.

■ Odp. e-y—-0,07 m.

^A

Rys. de ud. SM.

Rys. de ud. IW.

295. Przeprowadzić przez wicrzoholek D jednorodnego prostokąta ABCD prostą DE tak, aby po odoiędu części wzdłuż tej prostej I zawieszeniu pozostałego trapezu za wierzchołek £, bok AD o długości o znalazł się w położeniu poziomym.

Odp. ££-0,360 f.