IMG00138

I. Obliczenia wytrzymałościowe w przypadku obciążeń stałych

Tablica 10.1 (cd.)

Lp.	Schemat obciążenia	Wzory obliczeniowe
8		/ 3 . \ q x sin px x lx
		EJp^2 1,6/ p^2sinpl p^7l 6J q f sin px x\
	U-L-*	* ~ />^2 l sinpl I)’
		,, . „ 1 ( sinpA Mmax występuje dla x= —arc cos -— P V pl J

10.2. Pręty smukłe zginane i rozciągane

Linia ugięcia pręta smukłego poddanego rozciąganiu i zginaniu jest określona równaniem różniczkowym, analogicznym do równania (10. la)

EJ^-Ęr = M_x + Sy    (10.5)

dx

gdzie: EJ- sztywność pręta na zginanie, M_x- moment gnący od obciążeń poprzecznych (rys. 10.2), S - siła osiowa rozciągająca pręt.

y‘		_r
s		X—*■	T *

Rys. 10.2

Po wprowadzeniu oznaczenia (10.2) p² = SIEJ otrzymujemy równanie

d^

dx²

-P²y = P²

(10.6)

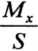
którego rozwiązanie ogólne ma postać

y = Cę^px + Dc^px + y_Q

gdzie: C, D - stałe całkowania wyznaczone z warunków brzegowych, e -podstawa logarytmów naturalnych, y₀ - całka szczególna równania (10.6).

138