img056

M₂. = 0,375P — l-OJSP-^-l = —0,0468 PI,

4    16

M.. = 0,375P- —/ —0,75P--r-/ = -0,0351 PI,

¹    8    64

M„ = 0.

Wykresy N_x, V_a, M, pokazano na rys. 3-42b, c, d.

Przykład 3-37. Sporządzić wykresy N_x, V₂ i M_x w parabolicznym luku trójprzegubo wym, obciążonym jak na rys. 3-43a. Strzałka łuku / = 1/4.

Rozpiętość łuku podzielono na 8 części (por. przykład 3-36). Wartości funkcji trygonomet rycznych w poszczególnych przekrojach łuku są takie same jak w przykładzie 3-36.

Warunki równowagi:

IX = H_a-H_b = 0,

zy=v_A- f+v_B = o,

o,

M_c=-Vb-j + H_b-\ = 0.

Z równań tych otrzymuje się:

h.-h.-j.y*-\ K-f-

Siły podłużne:

N?^c - — łysina—H_Acosx + pxsinoi.

Wartości sił N_x, otrzymane po podstawieniu danych, podano na rys. 3-43b. Siły poprzeczne:

V_x^c = V_Acosct — H_Asinoi — pxcosz, Ff^c = — F_Bcosa + H_gsina.

Wartości sił V_x, otrzymane po podstawieniu danych, podano na rys. 3-43c. Momenty zginające:

M

AC

CE

= V_AX-

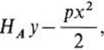
M°^c =V_B(l-x)-H_By.

Wartości momentów M_x, otrzymane po podstawieniu danych, podano na rys. 3-43d.

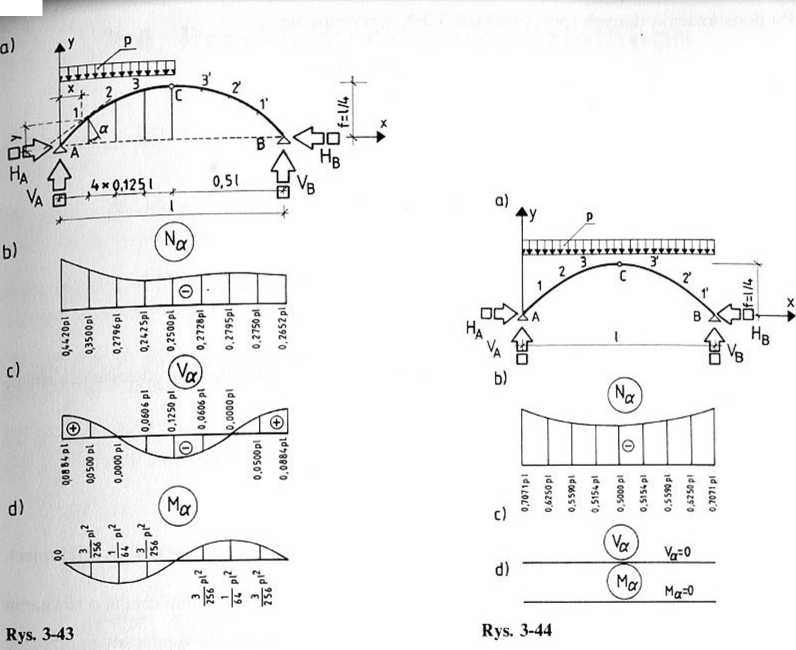
Przykład 3-38. Sporządzić wykresy sił podłużnych, sił poprzecznych i momentów zginających w łuku parabolicznym trójprzegubowym o równaniu jak w przykładzie 3-36, obciążonym równomiernie na całej rozpiętości (rys. 3-44a).

Równania równowagi:

IX = H _a — H_b = 0,

ZY= V_A+V_B-pl~0,

ZM_B=V_Al-pl-^ = 0,

I    pl l

Mc-yfJ-H.f-JJ-O-Po podstawieniu/= 0,25/ z równań tych otrzymano:

H_a = H_h

eL

2 ’

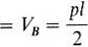
Siły podłużne:

JV'^,B = - łysina — //^cosa + p^sina.