mech2 38

74

75

dt

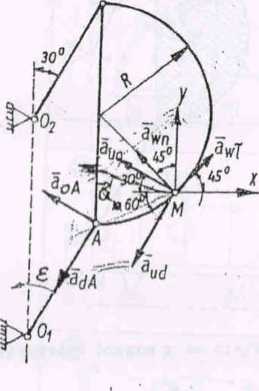
Hys. 48

+    = 312 om/s² .

Wyniki rozwiązania zadania zestawiono w tabeli 18.'

^a = "w ⁺ "u

lub w formie bardziej rozpisanej

j

^T= %r⁺ Sn ⁺ So ⁺ Sd-

Moduł wektora przyspieszenia względnego styoznego

\\4 ■ IW

dv    a

V⁼ 3T =

W rozpatrywanym przypadku

p    *

a^_r = 2n= 6,28 cm/s ,

= 6,28 om/s².

. . ;

Dodatni znak przy wielkości a_wT oznacza, że wektor    jefst zorientowany w stronę dodatniego zwrotu a^, tj. tak jak    (rya. 48).

Przyspieszenie względne normalne

s 16ir²    2    ?

Sn ⁼ TT = “1ó = ⁷¹    =9,87 om/B².

Wektor przyspieszenia a__ ma kierunek

wn

promienia,' a zwrot do środka krzywizny trajektorii ruchu względnego punktu M. Przyspieszenie unoszenia obrotowe

^o ^{= a}oA» ^aoA ⁼ °1^A * ^e »

gdzie e - moduł przyspieszenia kątowego członu O^A

e = | e | ,

~ d² cp

gdzie e = —- algebraiczna wielkość dt^

przyspieszenia kątowego.

W rozpatrywanym przypadku

e=    = 3,93 a ²*

Zgodność znaków wartości ? i ćo wskazuje, że obrót ciała D jest przyspieszony

= 20 • 3,93 = 79 cm/s².

Orientacja wektora a_UQ odpowiada kierunkowi a^_A (rys. 48). p_rZyspieszenie unoszenia doosiowe

2

®ud ^{= a}dA = °1^A * “² = ²⁰ ff⁷¹    = 31,25 n² = 308 cm/s².

Wektor "a^ ma zwrot od A do 0^, a a^ ma kierunek równoległy do

^dA*

Moduł przyspieszenia bezwzględnego znajdujemy metodą rzutowania:

Sc = ^(awr " ^awn^{} 003} *⁵° - ^10 ^{003 30}° - ®ud ^{008 60}°’

®y = ^^awr-^{+ a}wn^ ^{003 45}° ⁺ ®uo ^{008 60}° “ "ud ⁰⁰³ 3°°- .

Po wykonaniu obliozeA otrzymujemy

= - 225 om/a²,

, p

a^. = - 216 cm/s ,

’ ■ ^{a 3}    Y4

Tabela 18

: *p rad 1	a rad		Prędkość, om/a
			^Tu	^vw	^vx	_	V
^ ^71	7t TT	i™ •	78,5	12,6	-59,1	48,2	76,3

e			Przyspieszenie,		-5- cm/s
a"^2	*ud	^0	wn	®w *	^ax '	_!z_	a
4 ^71	308	79	10	6	-225	-216	312

e= 3,93 a"²,