mechanika123

Twierdzenie 3.2 (zasada zachowania pędu punktu materialnego)
Jeśli w przedziale t € (tA> iB) siła czynna jest równa zeru, to pęd punktu mali rialnego jest stały:
//{/) = const = //(rA) = H(ib) (3.15ł
Twierdzenie 3.3
Pochodna krętu punktu materialnego względem nieruchomego punktu O jcM równa momentowi siły czynnej względem tego punktu:
kQ(t) - M0(l) (3 K»
lwie rdzenie 3.6 (zasada równoważności pracy i energii kinetycznej)
Jeśli punki materialny nie znajduje się w polu potencjalnym, to praca siły i/ynnej w danym przedziale czasu jest równa przyrostowi energii kinetycznej punktu materialnego w tym przedziale:
L = *Ekt = Ek[tB)-Ek(tA) (3.22)
i‘nlc siłowe potencjalne
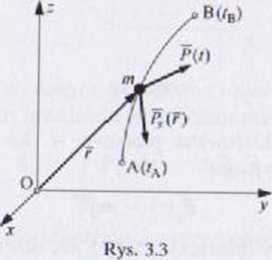
siłowym nazywamy obszar, w którym na punkt materialny działa doda-(kowa silą Ps(r) zależna tylko od położenia tego punktu (rys. 3.3):
P = /* e *P e +P e (3.23)
s * Si t sy y «vi v •
Twierdzenie 3.4 (zasada krętu punktu materialnego)
W danym przedziale czasu przyrost krętu punktu materialnego względem nimi chomego punktu O jest równy pokręlowi siły czynnej względem punktu O:
*Kq = A^ A*0 = *0{/B) - *0(rA) (3.17.
Twierdzenie 3.5 (zasada zachowiinia krętu punktu materialnego)
Jeśli w przedziale / e (rA, siła czynna jest równa zeru. to kręt punktu mnie rialnego względem nieruchomego punktu O jest stały:
*o(0 * 3 *<A> = *o«b>
Inne wielkości
W dynamice punktu materialnego definiuje się również następujące wielkoś* •
- praca siły czynnej w przedziale czasu r e (tA> tB):
•a %
L‘ f P dr = fp-vdt - f(Pxi*Pyy + Plź)dt [JJ
AB 'a
- energia kinetyczna punktu materialnego w chwili i:
£t(ł) = [3]
- moc chwilowa siły czynnej:
N(t) - h)-v<f) - PKi+P,y + Pti [W]
l‘ole siłowe jest potencjalne, jeśli istnieje pole skalarne Ep(r) takie, że:
P,|F).-grad Ef(r) =» Po- ^, />„
btfiie: Pjr) - P%[x, y, z) - siła potencjalna,
Ep(r) = Ep{Xy y, z) - energia potencjalna.
Pole siłowe potencjalne jest bezwirowe. tzn.
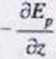
(3.24)
I « Ml
. i Ml
rot Pg{r)
0
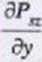
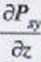
0
dPB dP<-
sx Tl
podstawowymi typami pól Ipoli sprężyste
dz dr
dr dy
siłowych potencjalnych
0 (3.25)
0
są: pole grawitacyjne
246
Dynamika. DulMawy uoi«iv»*l

Podstawy leoretytzne
247
Wyszukiwarka
Podobne podstrony:
materialnych, pęd i energia układu punktów materialnych, zasada zachowania pędu i energii mechaniczn
Zasada zachowania pędu. W odniesieniu do pojedynczego punktu materialnego drugą zasadę dynamiki
fizyka�9 1. Mechanika1.9. ZASADA ZACHOWANIA PĘDU A /1 = F At 1 zew Zmiana pędu A~p ukiadu ciał zacho
P1000884 Dynamika. Dynamika punktu materialnego. Prawa Newtona. Zasady zachowania dla punktu materia
81913 P1020482 Zasady zachowania dla punktu materialnego Zasada d’AIem berta Zasadniczerównanie dyna
P5070179 ZASADA ZACHOWANIA PĘDU Pęd układu pkt. materialnych można również nazwać ilością ruchu pkt.
SL272417 PĘD ZASADA ZACHOWANIA PĘDU 1
SL272417 PĘD ZASADA ZACHOWANIA PĘDU 1
ZASADA ZACHOWANIA PĘDU r ^ 1 Jeżeli na ciała oddziałujące
PĘD, ZASADA ZACHOWANIA PĘDU pęd jest iloczynem masy oraz prędkości p = rrrv popęd siły F-t = Ap F t
4. Zasada Zachowania Pędu
HPIM0591 Zasada zachowania pędu jeżeli - dt =0 wtedy ~p—const Jeżeli wypadkowa sił
DRGANIA MECHANICZNE -1 Napisz równanie ruchu drgającego punktu materialnego, który wykonuje drgania
więcej podobnych podstron