mechanika53

Pod u kład II: 3RRS

£* - 0:	p- h2~t3 - 0	M)
O ll W	N2 + N3 - 4Q = 0	(5)
M i^5 n o	N7[6b-f) + H2-2b-4Q2b P3b = 0	(6)

7*3 =

(5)    -t N^4Q-N_V r_j = n(4^-^)=O,15(4C>-iV₂)=O_ł6<?-0_t15A/₂ (4) =* P -(0,02ę +0.03Ay-(0,6Q-0,15AT₂) =0 =* P-0,62<?+0,12/V₂=0

(6)    —> N_? -(6b -Q,Q2b) + (0,02Q + 0,03N₂) • 2b 4Q- 2/3- P-3/> = 0 | :b

5,98/V₂ + 0,G4Q - 0,06A/j - 8<? 3P - 0 -3P-7,96<? ’6,04/V₂ - 0

Równania (4) i (6) tworzą układ równań z niewiadomymi P, W₂:

P 0,620+0,12^ = 0 |*3 -3P - 7_r96Q + 6,04N₂ = 0

-9,820 + 6,40A/₂ = 0 =

P = 0,620 -0,12M, = 0,620-0,12 1,530 = 0,440 Odp.: P^, = 0,440-

=> 6,40iV₂ = 9,820 | :6,40 -> JV₂ = l,53ę>

Zadanie 1.44

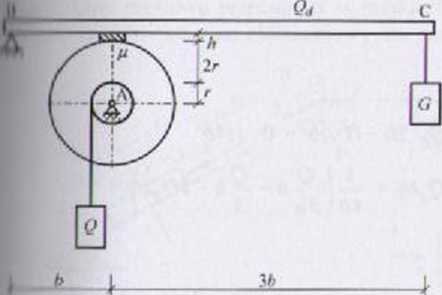
Dany jest hamulec tarczowy składający się z dwóch krążków sztywno ze soh.i połączonych, podpartych przegubowo w punkcie A, dźwigni BC i klock i o wysokości h, sztywno połączonego z dźwignią. Na mniejszy krążek nawinięta jest lina. na której zawieszono blok o ciężarze Q. Na końcu dźwigni zawieszony jest blok o nieznanym ciężarze G. Wyznaczyć minimalną wartuj ciężaru G, przy której układ pozostaje w równowadze statycznej. Uwzględni*.' tarcie ślizgowe klocka o krążek duży. Dźwignia jest prętem pryzmatycznym o ciężarze Q_d. Ciężar lin pominąć.

106

Staiykn. 1 2.J. Równowagi graniczna mechanizmów pliwkich / larciciii

Dane: Q

Qi

n

r

h

b

IwMif/f mie

l'M • > jest w równowadze statycznej przy G z G_n;in. Po przekroczeniu równo-granicznej ((7 ^{< C}min) krążki zaczną obracać się przeciwnie do mchu ■fcji/ńwek zegara. W zadaniu nie podano cię/.aru krążków Q_k, a więc nic WWni wyznaczyć reakcji na podporze A. Schemat obliczeniowy ma postać:

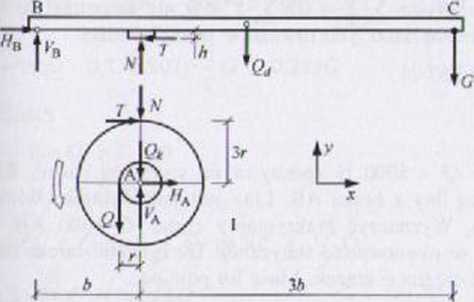
hmikład I: 3RRS ^ V 0

) Y * 0

) M_a - 0: Q r-T 3r - 0 |:r

»/<?=> 3p/v = £> => /V = -2., t = \iN - Q

3p    3

107

WiHnU 1.2.3. Równowaga graniczna incchnni/mów pińskich /. tarciem