mechanika54

Poduldad II: 3RRS

E^x - o E^Y* 0

M_B = 0: N-b-Th-Q_H-2b-G-4b - 0 |:4/>

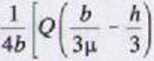
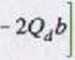
Przykładowe dane:

r = 0,2 m - 566,67 N

<? = 2 kN = 2000 N, = 500 N, \i = 0,2,

h = 5 cm = 0,05 m.		b - 0,5 m
a - ^1	2000-	0,5	0,5
^ 4 0,5		3-0,2	3

Uwaga: Równania typu J2 % ⁼ 0* 5Z ^ ⁼ 0 nie są potrzebne do wyznać/o nia G_mia, stąd nie zapisano tycłi równań w jawnej postaci.

Odp.: G^ = 566,67 N.

Zadanie 1.45

Blok o ciężarze Q = 5000 N spoczywa na szorstkiej równi. Blok ten połą czono za pomocą liny z. belką AB. Lina jest jednokrotnie owinięta na niem chomym krążku. Wyznaczyć maksymalny ciężar G belki AB. przy którym układ pozostaje w równowadze statycznej. Uwzględnić tarcie ślizgowe bloku o równię i tarcie cięgna o krążek. Masę lin pominąć.

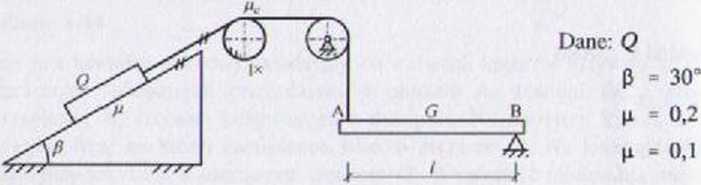
Rozwiązanie

Układ jest w równowadze statycznej przy G_Illln s G s G_nM. Po przekroczę niu górnego punktu równowagi granicznej tG > C^) nastąpi ruch bloku Q

108

Statyka. 1.2.3. K(Vwnown)fii ^r* niemi mechanizmów |tła\kii/h z tarciom

i piuwo. Liny myślowo przecinamy w punktach styku z ciałami sztywnymi, naciągi. Schemat obliczeniowy ma postać:

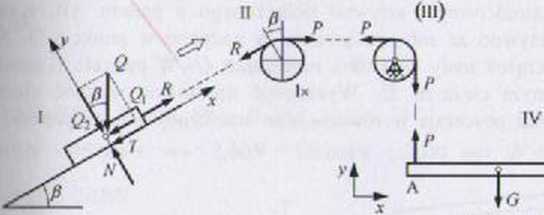
ftnliiklad IV: 2RRS

> * ⁰

V U = 0: G - - P I = 0 => P - -G

Hotluklatl II (cięgno owinięte na krążku)

i ■ [i • 360" = 30“ * 360“ = 390“ - 390“ • — - 6,807 rad

180”

(I-c ' “P = exp( -0,1 -6,807) ■ ~G = 0.253G ■kluk lud I: 2RRS

0:    R-Q, -T = 0    (I)

V 0:    *-<?,= 0    (2)

|ll ■=» N - Q₂ - (?cosP - Qcos30” - ^Q

Tl

t - \lN = 0,2= 0,1

III R = O, ⁺ r ==» R = Osinp /' C? sin 30^ + T

II M3G =    * 0,1

U..'13C « 0.673C? |:0,253

fi *    = 2,660,    = 2,660 = 2,66*5000 - 13300 N

iMp.j - 13300 N.

109

bniyk.i 1.2.3 Równowago graniczna mechanizmów płaskich / tarciem